GT考试 BZOJ 1009
GT考试
【问题描述】
阿申准备报名参加GT考试，准考证号为N位数X1X2....Xn(0<=Xi<=9)，他不希望准考证号上出现不吉利的数字。
他的不吉利数学A1A2...Am(0<=Ai<=9)有M位，不出现是指X1X2...Xn中没有恰好一段等于A1A2...Am. A1和X1可以为0
【输入格式】
第一行输入N,M,K.接下来一行输入M位的数。
【输出格式】
阿申想知道不出现不吉利数字的号码有多少种，输出模K取余的结果.
【样例输入】
4 3 100
111
【样例输出】
81
【数据范围】
N<=10^9， M<=20， K<=1000
题解：
设f[i][j]表示至准考证号前i位，最多匹配到不吉利数的第j位的方案数
设a[i][j]表示在不吉利数的前i位后加上一个字符能匹配到不吉利数的第j位的字符的数量（枚举字符用KMP求出a矩阵）
那么转移方程：
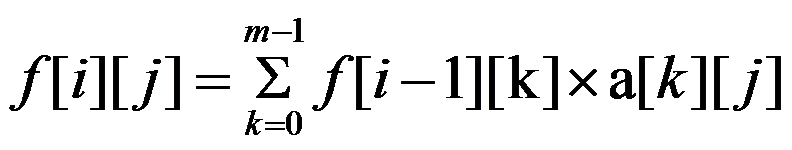
答案：
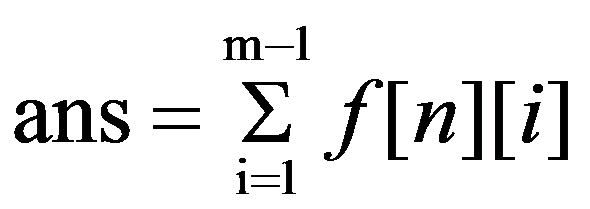
发现转移方程可以用矩阵乘法优化
1 #include<algorithm>
2 #include<iostream>
3 #include<cstring>
4 #include<cstdlib>
5 #include<cstdio>
6 using namespace std;
7 int n, m, t, mo, sum, s[25], ne[25];
8 struct ccc
9 {
10 int v[25][25];
11 ccc()
12 {
13 memset(v, 0, sizeof(v));
14 }
15 friend ccc operator * (ccc a, ccc b)
16 {
17 ccc ans;
18 for(int i = 0; i < m; ++i)
19 for(int j = 0; j < m; ++j)
20 for(int k = 0; k < m; ++k)
21 ans.v[i][j] = (ans.v[i][j] + a.v[i][k] * b.v[k][j]) % mo;
22 return ans;
23 }
24 friend ccc operator ^ (ccc a, int b)
25 {
26 ccc ans;
27 for(int i = 0; i <= m; ++i) ans.v[i][i] = 1;
28 for(int i = b; i; i >>= 1, a = a * a)
29 if(i & 1)
30 ans = ans * a;
31 return ans;
32 }
33 };
34 ccc a, c;
35 int main()
36 {
37 scanf("%d%d%d", &n, &m, &mo);
38 getchar();
39 for(int i = 1; i <= m; ++i) s[i] = getchar() - '0';
40 t = 0;
41 for(int i = 2; i <= m; ++i)
42 {
43 while(t > 0 && s[i] != s[t + 1]) t = ne[t];
44 if(s[i] == s[t + 1]) ++t;
45 ne[i] = t;
46 }
47 for(int i = 0; i < m; ++i)
48 for(int j = 0; j <= 9; ++j)
49 {
50 t = i;
51 while(t > 0 && s[t + 1] != j) t = ne[t];
52 if(s[t + 1] == j) ++t;
53 if(t != m) a.v[t][i] = (a.v[t][i] + 1) % mo;
54 }
55 for(int i = 0; i < m; ++i)
56 {
57 for(int j = 0; j < m; ++j)
58 printf("%d ", a.v[i][j]);
59 printf("\n");
60 }
61 c = a ^ n;
62 for(int i = 0; i < m; ++i) sum = (sum + c.v[i][0]) % mo;
63 printf("%d", sum);
64 }
