防线修建 BZOJ 2300
防线修建
【问题描述】
近来A国和B国的矛盾激化,为了预防不测,A国准备修建一条长长的防线,当然修建防线的话,肯定要把需要保护的城市修在防线内部了。可是A国上层现在还犹豫不决,到底该把哪些城市作为保护对象呢?又由于A国的经费有限,所以希望你能帮忙完成如下的一个任务:
1.给出你所有的A国城市坐标
2.A国上层经过讨论,考虑到经济问题,决定取消对i城市的保护,也就是说i城市不需要在防线内了
3.A国上层询问对于剩下要保护的城市,修建防线的总经费最少是多少
你需要对每次询问作出回答。注意单位1长度的防线花费为1。
A国的地形是这样的,形如下图,x轴是一条河流,相当于一条天然防线,不需要你再修建
A国总是有两个城市在河边,一个点是(0,0),一个点是(n,0),其余所有点的横坐标均大于0小于n,纵坐标均大于0。A国有一个不在(0,0)和(n,0)的首都。
(0,0),(n,0)和首都这三个城市是一定需要保护的。
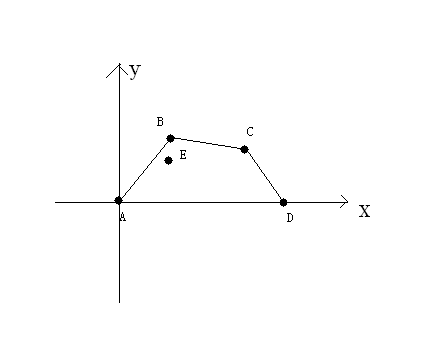
上图中,A,B,C,D,E点为A国城市,且目前都要保护,那么修建的防线就会是A-B-C-D,花费也就是线段AB的长度+线段BC的长度+线段CD的长度
如果,这个时候撤销B点的保护,那么防线变成下图

【输入格式】
第一行,三个整数n,x,y分别表示河边城市和首都是(0,0),(n,0),(x,y)。
第二行,一个整数m。
接下来m行,每行两个整数a,b表示A国的一个非首都非河边城市的坐标为(a,b)。
再接下来一个整数q,表示修改和询问总数。
接下来q行每行要么形如1 i,要么形如2,分别表示撤销第i个城市的保护和询问。
【输出格式】
对于每个询问输出1行,一个实数v,表示修建防线的花费,保留两位小数
【样例输入】
4 2 1
2
1 2
3 2
5
2
1 1
2
1 2
2
【样例输出】
6.47
5.84
4.47
【数据范围】
30%的数据m<=1000,q<=1000
100%的数据m<=100000,q<=200000,n>1
所有点的坐标范围均在10000以内, 数据保证没有重点
题解:
题意即为支持删点维护一个上凸壳
由于只需要支持删点的操作
那么离线倒序处理,就变为加点操作
若要加入的点在凸包内,那就把它丢掉······
如果这个点在凸包外
分别考虑这个点左右两边的点
向两个方向维护上凸壳
这个过程用set实现
1 #include<algorithm>
2 #include<iostream>
3 #include<cstring>
4 #include<cstdlib>
5 #include<cstdio>
6 #include<cmath>
7 #include<set>
8 using namespace std;
9 inline int Get()
10 {
11 int x = 0;
12 char c = getchar();
13 while('0' > c || c > '9') c = getchar();
14 while('0' <= c && c <= '9')
15 {
16 x = (x << 3) + (x << 1) + c - '0';
17 c = getchar();
18 }
19 return x;
20 }
21 const int me = 200233;
22 int n, m, x, y, e;
23 int nu;
24 double sum;
25 struct dot
26 {
27 int x, y;
28 inline bool operator < (const dot &z) const
29 {
30 if(x != z.x) return x < z.x;
31 return y < z.y;
32 }
33 };
34 dot o;
35 dot a[me];
36 int flag[me];
37 bool vis[me];
38 int num[me];
39 double ans[me];
40 multiset<dot> c;
41 inline double Dis(const int &ax, const int &ay, const int &bx, const int &by)
42 {
43 return sqrt((ax - bx) * (ax - bx) + (ay - by) * (ay - by));
44 }
45 inline int Cross(const int &ax, const int &ay, const int &bx, const int &by)
46 {
47 return ax * by - bx * ay;
48 }
49 inline void Add(dot v)
50 {
51 multiset<dot>::iterator l = c.upper_bound(v), r = l;
52 --l;
53 if(Cross((r -> x) - (l -> x), (r -> y) - (l -> y), v.x - (l -> x), v.y - (l -> y)) <= 0) return;
54 sum -= Dis((l -> x), (l -> y), (r -> x), (r -> y));
55 multiset<dot>::iterator now;
56 while(l != c.begin())
57 {
58 now = l;
59 --l;
60 if(Cross(v.x - (l -> x), v.y - (l -> y), (now -> x) - (l -> x), (now -> y) - (l -> y)) >= 0)
61 {
62 ++l;
63 break;
64 }
65 sum -= Dis((now -> x), (now -> y), (l -> x), (l -> y));
66 c.erase(now);
67 }
68 while(true)
69 {
70 now = r;
71 ++r;
72 if(r == c.end())
73 {
74 --r;
75 break;
76 }
77 if(Cross(v.x - (r -> x), v.y - (r -> y), (now -> x) - (r -> x), (now -> y) - (r -> y)) <= 0)
78 {
79 --r;
80 break;
81 }
82 sum -= Dis((now -> x), (now -> y), (r -> x), (r -> y));
83 c.erase(now);
84 }
85 c.insert(v);
86 sum += Dis((l -> x), (l -> y), v.x, v.y) + Dis(v.x, v.y, (r -> x), (r -> y));
87 }
88 int main()
89 {
90 o.x = o.y = 0;
91 c.insert(o);
92 o.x = n = Get();
93 c.insert(o);
94 o.x = x = Get();
95 o.y = y = Get();
96 c.insert(o);
97 m = Get();
98 sum = Dis(0, 0, x, y) + Dis(x, y, n, 0);
99 for(int i = 1; i <= m; ++i)
100 {
101 a[i].x = Get();
102 a[i].y = Get();
103 }
104 e = Get();
105 for(int i = 1; i <= e; ++i)
106 {
107 flag[i] = Get();
108 if(flag[i] == 1)
109 {
110 num[i] = Get();
111 vis[num[i]] = true;
112 }
113 }
114 for(int i = 1; i <= m; ++i)
115 if(!vis[i])
116 Add(a[i]);
117 for(int i = e; i >= 1; --i)
118 {
119 if(flag[i] == 1) Add(a[num[i]]);
120 else ans[++nu] = sum;
121 }
122 for(int i = nu; i >= 1; --i)
123 printf("%.2lf\n", ans[i]);
124 }



