【深度学习】梯度下降算法和随机梯度下降算法
导语
梯度是神经网络中最为核心的概念,在介绍梯度之前我们要先知道数学中的导数以及偏微分的理论概念。
导数
这里套用维基百科上的介绍,导数描述了函数在某一点附件的变化率,导数的本质是通过极限对函数进行局部的线性逼近,当函数\(f\)的自变量在一点\(x_0\)上产生一个增量\(△x\)时,则函数值的增量\(△y\)与自变量的增量\(△x\)的比值在\(△x\)趋于0时的极限存在,即为\(f\)在\(x_0\)处的导数,记为\(f'(x_0)\)、\(\frac{df}{dx}(x_0)\)或\(\frac{\text{d}y}{\text{d}y}\mid_{x = x_0}\)。
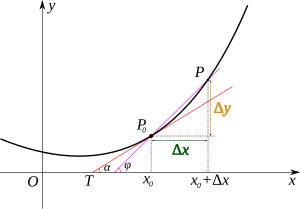
当函数定义域和取值都在实数域中的时候,函数在某一点的导数就是该函数所代表的曲线在这一点上的切线斜率。如下图所示,设\({P_0}\)为曲线上的一个定点,\(P\)为曲线上的一个动点。当\(P\)沿曲线逐渐趋向于点\({P_0}\)时,并且割线\(P P_0\)的极限位置\(P_0 T\)存在,则称\(P_0 T\)为曲线在\(P_0\)处的切线。
偏导数
在数学中,一个多变量的函数的偏导数是它关于其中一个变量的导数,而保持其他变量恒定。
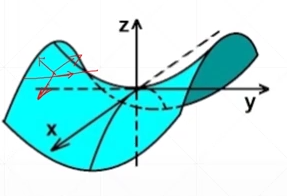
假设f是一个多元函数\(z=f(x,y)=y^2-x^2\),如图所示,则函数z关于x和y的偏导数分别为\(\frac{\partial z}{\partial x}=-2x\)、\(\frac{\partial z}{\partial y}=2y\)
梯度
而梯度则是多元函数中所有关于自变量偏导数的向量:\(\bigtriangledown f=(\frac{\partial f}{\partial x_1};\frac{\partial f}{\partial x_2};...;\frac{\partial f}{\partial x_n})\)
梯度是一个向量,指向函数值上升最快的方向,显然,梯度的反方向当然就是函数值下降最快的方向了,这也是梯度下降算法的主要思想。
损失函数
对于监督学习,由训练样本的特征\(X\),label实际值\(y\),根据模型\(h(x)\)计算得出预测值\(\hat{y}\),一个好的计算模型当然是\(\hat{y}\)和\(y\)越接近越好,数学上有很多方法来表示\(\hat{y}\)和\(y\)的接近程度,在深度学习中,主要以损失函数(loss)这个概念来表示预测值\(\hat{y}\)与实际值\(y\)的差距。
在训练神经网络的目的是要损失误差函数尽可能的小,即求解weights使误差函数尽可能小。首先随机初始化weights,然后不断反复更新weights使得误差函数减小。通过改变神经网络中所有的参数(寻找最优权重参数),使得损失函数不断减小,从而训练出更高准确率的神经网络模型。
常见的损失函数有均方误差和交叉熵误差,损失函数一个以权重参数为自变量的函数。
线性模型
输出\(y=h(x)=w^Tx\),类似这样的就是线性模型,输出\(y\)就是输入特征\(x_1,x_2,...\)的线性组合。下面介绍的三种梯度下降都是以线性回归算法来进行比较的。
均方误差
\(\frac{1}{2}\)是为了求导方便。
梯度下降算法
对于神经网络模型来说,如何能达到高准确率的效果,其关键在于不断优化目标损失函数,找到近似最优权重参数,使得预测估计值不断逼近真实值。
在数学中,我们可以求得函数\(y=f(x)\)的极值点,也就求它的导数\(f'(x)=0\)的那个点。因此可以通过解方程\(f'(x)=0\),求得函数的极值点\((x_0,y_0)\)
但是计算机不想人脑一样,可以解方程。但是它可以凭借强大的计算能力,一步一步的把函数的极值点试出来。如下图所示,首先随机选择一点开始比如\(x_0\),然后通过步长不断迭代修改\(x\)后达到\(x_1,x_2,x_3,....\),经过数次迭代后会达到函数的最小值点。

像上面找到最小值点,在神经网络中也就是通过梯度的相反方向来修改\(x\),而每次修改的幅度也就是移动步长也需要选择合适,如果选择小了,那么就会迭代很多轮才能走到最小值附近;如果选择大了,那可能就会越过最小值很远,收敛不到一个好的点上。
批梯度下降(Batch Gradient Descent)算法
因此,经过上面的讨论,可以写出梯度下降算法的公式:
其中\(\nabla\)是梯度算子;\(\nabla f(x)\)就是指\(f(x)\)的梯度;\(\eta\)是步长,也称作学习速率,表示每次向着函数最陡峭方向迈步。
这里为了推导方便,神经网络模型使用的是最简单的一种\(y=wx\),没有偏置也没有激活函数。
下面详细推导 梯度\(\nabla E(w)\)的过程。由于公式打完可能会吐血,我就上传手写笔记了(-字有点丑)。

所以,最后梯度下降算法的最终呈现形式:
每次参数更新的伪代码如下:
repeat{
\(W_{new_i}=W_{old_i}+\eta \sum_{i=1}^{n}(y^{(i)}-\hat{y}^{(i)})x^{(i)}\)
(for every j=0,...,n)
}
随机梯度下降收敛图如下:
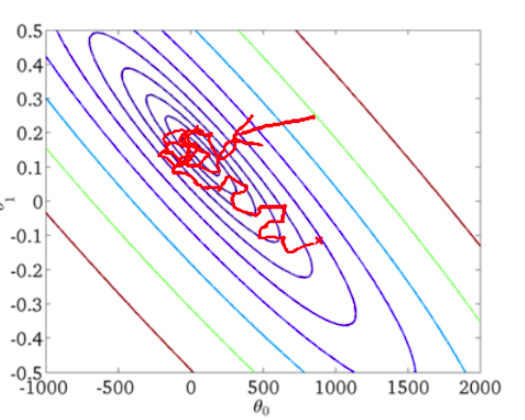
从图中可以看出SGD迭代的次数较多,在解空间的搜索过程看起来很盲目,但是大体上是往着最优值方向移动。
根据上面的式子训练模型,每次更新迭代参数\(w\),要遍历训练计算数据中的所有样本(\(\sum\)),这种算法叫做批梯度下降(Batch Gradient Descent)。但如果样本数量十分庞大,则会造成计算量异常巨大,这时候就推荐使用随机梯度下降算法(Stochastic Gradient Descent, SGD)。
批梯度下降的收敛图如下:
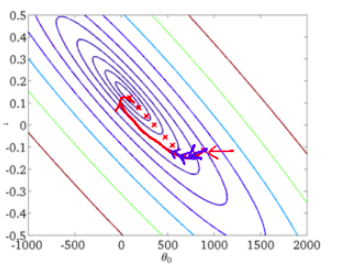
从图中,可以得到BGD的迭代次数相对较少。
随机梯度下降算法(Stochastic Gradient Descent, SGD)
由于批梯度下降每跟新一个参数的时候,要用到所有的样本数,所以训练速度会随着样本数量的增加而变得非常缓慢。随机梯度下降正是为了解决这个办法而提出的。
具体而言,在算法的每一步,我们从训练集中均匀抽出一 小批量( minibatch) 样本\(B = fx(1); : : : ; x(m′)g\)。 小批量的数目 m′ 通常是一个相对较小的数,从一到几百。重要的是,当训练集大小 m 增长时, m′ 通常是固定的。我们可能在拟合几十亿的样本时,每次更新计算只用到几百个样本。
这时的梯度估计可以表示为:
pytorch关于梯度的相关API:
- torch.autograd(loss,[w1,w2,...])
-[w1 grad, w2 grad...] - los.backward()
-w1.grad
-w2.grad
参考教程:
https://www.zybuluo.com/hanbingtao/note/448086
https://zhuanlan.zhihu.com/p/25765735


