Codeforces 405 E. Graph Cutting （ DFS ）

 

题意：

给n个点，m条边，将这个图拆成多个子图，每个子图里面有两条相邻的边（也就是每个子图 3个点2条边），当然每条边只能属于一个子图，如果不能拆分成功，则No solution， 否则，将每个子图的3个顶点（x，y，z）输出 （这个子图包含 x到y 的边 ， y到z的边 ）

思路：
m是奇数，则不能拆分。
m是偶数，可以拆分。

1、将图形看成以1为树根的一棵“树”，这棵树会有环，把它当成一颗简单树来分析思路，如下图的一棵树。
　　题目中的是无向图，画图的时候不小心画成了有向的了，，，，，（只要把它当成无向就好了，忽视箭头就好了）



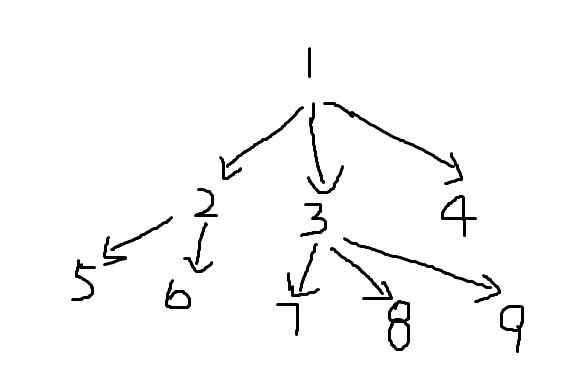
2、从树根 1 开始遍历，一直到叶子节点（或者遇到已经被访问过的点），然后进行一些操作，然后回溯。
操作为：
给每个点一个队列来存放它的可用的子节点（存进去的可用的子节点，指的是这个点到子节点的边还未用过）。
然后让这些可用的子节点两两一对，（即child1，root，child2 为一个子图 ）。
　　如果可用的子节点为奇数，则说明有一条到子节点的边没有被用过，则另外需要当前这个点到它父亲节点的一条边，使之构成一个子图。
例如 图中的 节点3 ： 它有3个子节点，（6—3—8）一个子图，3—9这条边则需要和3—1这条边组成一个子图（1—3—9），所以节点3这个点不再是节点1的可用的子节点了，因为1—3 这条边已经被用过了。
　　如果可用的子节点是偶数，则不需要直接构成子图就好了。当然这个节点仍然是它父亲节点的可用子节点。如节点2仍然是节点1的子节点。

#include<stdio.h>
#include<string.h>
#include<iostream>
#include<algorithm>
#include<vector>
#include<queue>

using namespace std;

const int T=1e5+5;

struct node
{
    int x,num;
}t;

vector < node > Q[T];
bool flag[T];

int dfs( int now )
{
    int l=(int)Q[now].size(),r,v1,v2;
    node k;
    queue < int > q;   // 注意==>是每个节点都有一个队列
    for(int i=0;i<l;i++)
    {
        k=Q[now][i];
        if( flag[k.num] ) continue;
        flag[k.num]=1;
        r = dfs( k.x );
        if( r ) printf("%d %d %d\n",now,k.x,r); // 说明 now 节点的子节点有一条未用的边
        else q.push( k.x );  //否则将这个节点存入到队列里
    }
    while( q.size() >= 2 )
    {
        v1=q.front();
        q.pop();
        v2=q.front();
        q.pop();
        printf("%d %d %d\n",v1,now,v2);
    }
    if( !q.empty() )
    {
        v1=q.front();
        return v1;  // 如果队列里面有剩余，则将此队列里的点返回回去和其父节点，父节点的父节点构成一个子图
    }
    return 0;
}

int main( )
{
    int n,m,a,b;
    while(~scanf("%d%d",&n,&m))
    {
        for(int i=0;i<=n;i++)
            Q[i].clear();
        for(int i=1;i<=m;i++)
        {
            scanf("%d%d",&a,&b);
            t.num=i;
            t.x=b;
            Q[a].push_back( t );
            t.x=a;
            Q[b].push_back( t );
        }
        if( m%2 ) printf("No solution\n");
        else{

            memset(flag,0,sizeof(flag));
            dfs( 1);
        }
    }
    return 0;
}