二叉树的生成和遍历
二叉树是一种树状结构的图。它由一系列节点和边组成。
每个节点的字节点数不超过2个,只有一个根结点。
基础名词解释
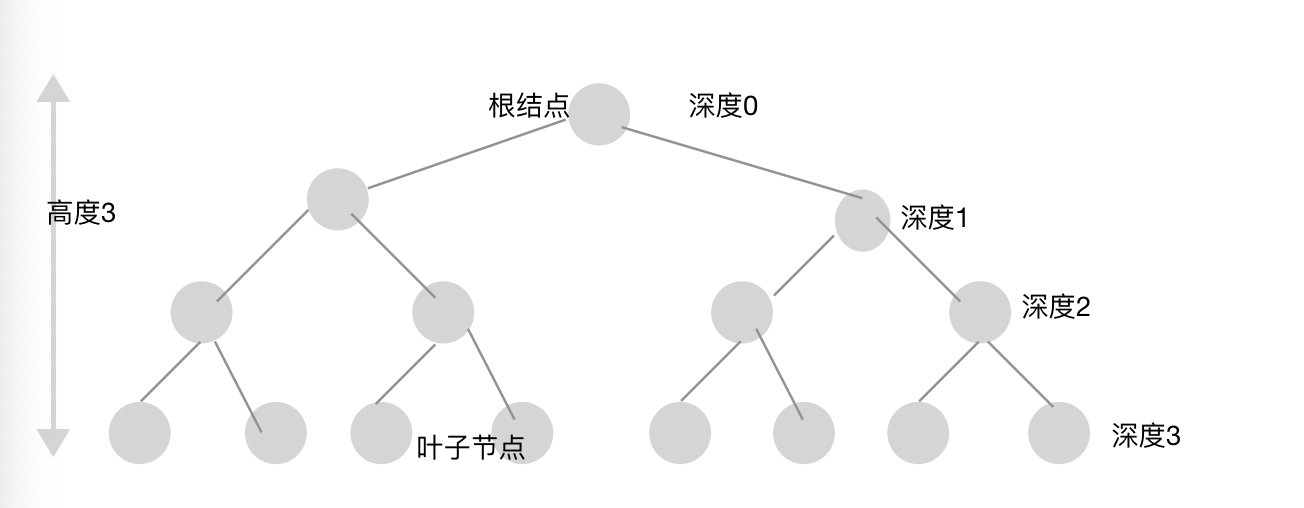
度: 每个节点的字节点的个数。如图:每个节点的度都是2。如果某个节点有一个字节点,那么它的度是1。
根节点: 一棵树最上面的节点;一棵树只有一个根节点。
叶子节点: 没有字节点的节点。图中最下面的8个节点都是叶子节点。
高度: 树的层数。图中树的高度是3。
深度: 节点所处的深度;叶子节点的深度等于树的高度;根结点是深度0, 依次类推,字节点是深度1...
内部节点: 除了叶子节点以外的节点。图中除了最下面的8个叶子节点之外的7个节点都是内部节点。包含根结点。
树的分类
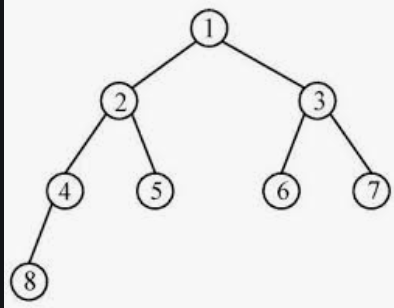
满二叉树: 满二叉树要求高度为h的二叉树总节点数为2**(n+1)-1的。上面的示意图是个满二叉树。
完全二叉树: 完全二叉树只要求从1-n的节点排布同满二叉树。
二叉查找树: 对于所有的节点来说,当前节点的左子树的所有节点的值比当前节点的值要小;
所有右子树的值比当前节点的值要大。下图是个查找二叉树。
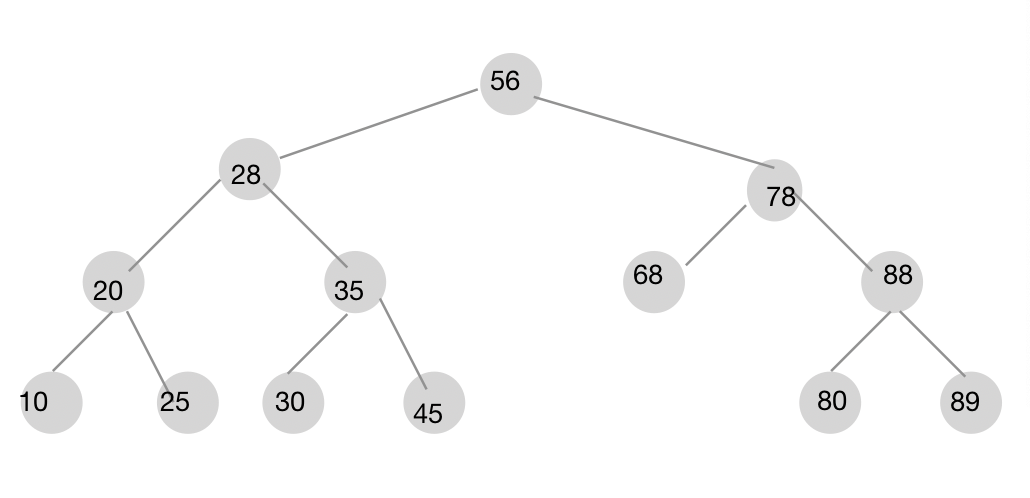
二叉查找树遍历方式
中序遍历: 即按照数据升序遍历。按照左子节点,父结点,右子节点的顺序遍历。
然后对于根节点来说,左右子节点本身又是个二叉查找树,需要递归调用,直到叶子节点为止。
叶子节点相当于左右子节点都是null的节点。
先序遍历:按照根结点,左子树,右子树的顺序遍历。
后序遍历:按照左子树,右子树,根结点的顺序遍历。
使用代码实现如下:
<!-- * @Author: LyraLee * @Date: 2019-10-30 08:53:28 * @LastEditTime: 2019-11-04 11:57:19 * @Description: 二叉树的生成和遍历方法 --> <!DOCTYPE html> <html lang="en"> <head> <meta charset="UTF-8"> <meta name="viewport" content="width=device-width, initial-scale=1.0"> <meta http-equiv="X-UA-Compatible" content="ie=edge"> <title>二叉树的生成和遍历方法</title> </head> <body> <script type="module"> // 节点的构造函数 function Node(data, left, right) { this.data = data; this.left = left; this.right = right; } // 二叉树向某节点插入数据--向某个父节点的左子节点或者右子节点插入数据 function insert (data) { let newNode = new Node(data, null, null); if (this.root === null) { this.root = newNode; } else { let current = this.root; let parent; while(true) { //从根节点查找,循环查找需要插入的位置 let parent = current; if (current.data > data) { current = current.left; if (current === null) { parent.left = newNode; //插入成功 break; } } else { current = current.right; if (current === null) { parent.right = newNode; // 插入成功 break; } } } } } // 二叉查找树的构造函数 function BST() { this.root = null; //根节点 this.insert = insert; this.inOrder = inOrder; this.preOrder = preOrder; this.postOrder = postOrder; } // 中序遍历--升序--左->根->右 let arrIn = []; let inOrder = function(node) { if (node !== null) { inOrder(node.left); arrIn.push(node.data); inOrder(node.right); } } // 先序遍历--根->左->右 let arrPre = []; let preOrder = function(node) { if (node !== null) { arrPre.push(node.data); preOrder(node.left); preOrder(node.right); } } // 后续遍历--左->右->根 let arrPost = []; let postOrder = function(node) { if (node !== null) { postOrder(node.left); postOrder(node.right); arrPost.push(node.data); } } let data = [56,28,78,20,35,68,88,10,25,30,45,80,89]; const bst = new BST(); data.forEach(i => bst.insert(i)) bst.inOrder(bst.root); console.log('inOrder-->',arrIn); bst.preOrder(bst.root); console.log('preOrder-->',arrPre); bst.postOrder(bst.root); console.log('postOrder-->',arrPost); </script> </body> </html>
运行结果如下:
// 运行结果如下: inOrder-->[10, 20, 25, 28, 30, 35, 45, 56, 68, 78, 80, 88, 89] preOrder-->[56, 28, 20, 10, 25, 35, 30, 45, 78, 68, 88, 80, 89] postOrder-->[10, 25, 20, 30, 45, 35, 28, 68, 80, 89, 88, 78, 56]



