梯度下降法和牛顿法的总结与比较

机器学习的本质是建立优化模型，通过优化方法，不断迭代参数向量，找到使目标函数最优的参数向量。最终建立模型

通常用到的优化方法：梯度下降方法、牛顿法、拟牛顿法等。这些优化方法的本质就是在更新参数。

一、梯度下降法

　　0、梯度下降的思想

·　　　　通过搜索方向和步长来对参数进行更新。其中搜索方向是目标函数在当前位置的负梯度方向。因为这个方向是最快的下降方向。步长确定了沿着这个搜索方向下降的大小。

　　　　迭代的过程就像是在不断的下坡，最终到达坡地。

　　　　接下来的目标函数以线性回归的目标函数为例：

　　　　

　　　　

 

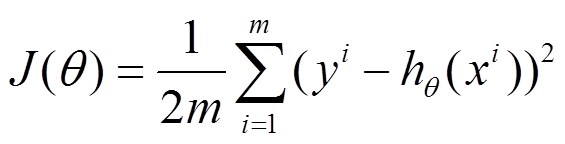
　　1、批量梯度下降法

　　　　

　　　　

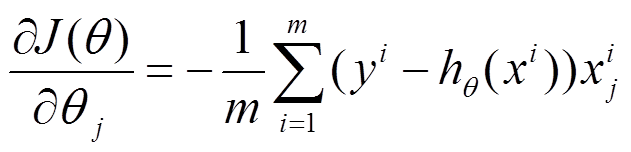
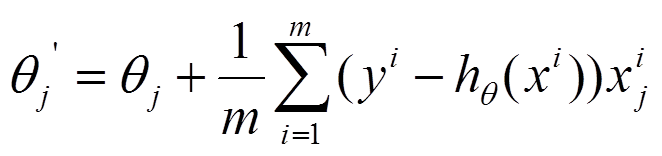
　　　　参数更新是要用到全部样本。如上式中的m

　　2、随机梯度下降法

　　　　

　　　　

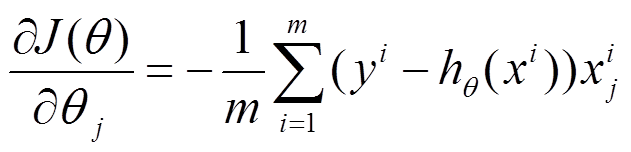
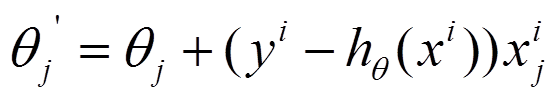
　　　　参数的更新只用到某一个样本。而不是全部的样本。批量梯度下降公式中的m变为了1

　　3.随机梯度下降和梯度下降的比较

　　　　批量梯度下降：1.是最小化所有样本的损失函数，最终得到全局最优解。

　　　　　　　　　　　2.由于每次更新参数需要重新训练一次全部的样本，代价比较大，适用于小规模样本训练的情况。

　　　　随机梯度下降：1.是最优化每个样本的损失函数。每一次迭代得到的损失函数不是，每次每次向着全局最优的方向，但是大体是向着全局最优，最终的结果往往是在最优解的附近。

　　　　　　　　　　　2.当目标函数是凸函数的时候，结果一定是全局最优解。

　　　　　　　　　　　3.适合大规模样本训练的情况。

　　3、小批量梯度下降法

　　　　将上述两种方法作结合。每次利用一小部分数据更新迭代参数。即样本在1和m之间。

二、牛顿法

　　　　首先牛顿法是求解函数值为0时的自变量取值的方法。

　　　　利用牛顿法求解目标函数的最小值其实是转化成求使目标函数的一阶导为0的参数值。这一转换的理论依据是，函数的极值点处的一阶导数为0.

　　　　其迭代过程是在当前位置x0求该函数的切线，该切线和x轴的交点x1，作为新的x0,重复这个过程，直到交点和函数的零点重合。此时的参数值就是使得目标函数取得极值的参数值。

　　　　其迭代过程如下：

　　　　

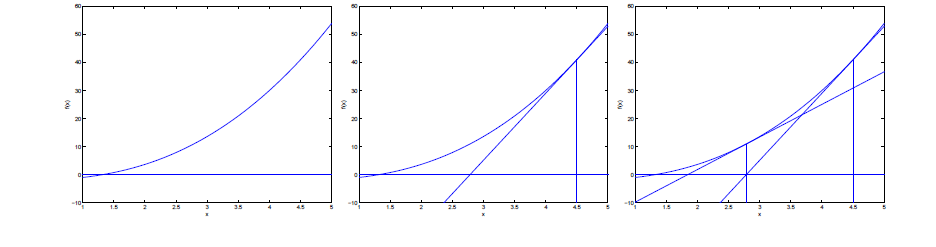
　　迭代的公式如下：

　　

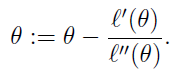
　　当θ是向量时，牛顿法可以使用下面式子表示：

 　　

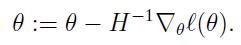
　　 其中H叫做海森矩阵，其实就是目标函数对参数θ的二阶导数。

三、牛顿法和梯度下降法的比较

　　1.牛顿法：是通过求解目标函数的一阶导数为0时的参数，进而求出目标函数最小值时的参数。

　　　　　　　收敛速度很快。

　　　　　　　海森矩阵的逆在迭代过程中不断减小，可以起到逐步减小步长的效果。

　　　　　　　缺点：海森矩阵的逆计算复杂，代价比较大，因此有了拟牛顿法。

　　2.梯度下降法：是通过梯度方向和步长，直接求解目标函数的最小值时的参数。

　　　　　　　　　越接近最优值时，步长应该不断减小，否则会在最优值附近来回震荡。