17.10.24 数据最水的一次考试
A + 35 + 0
总结:
总的来说这次考试的测试数据有点垃lj,
T1 n <= 1e5, 然而n ^ 2都是可以过的
T2 感觉 k 就是个lj,没有啥用,首先对于k=1的情况,可以枚举每条q边
即使直接跑最短路也可以过 60%,对于最后30%,实际数据k >= n,然而没仔细看(理解)数据范围。
数组开小了,丢了40‘;
T3 难。
1.每道题都要看数据范围,看看有没有好骗分的lj数据
2.不要开不够数组!!!!!!!!!!!!!!!!!!!!!!!!
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
题目描述
现在有一个字符串,每个字母出现的次数均为偶数。接下来我们把第一次出现的字母a和第二次出现的a连一条线,第三次出现的和四次出现的字母a连一条线,第五次出现的和六次出现的字母a连一条线...对其他25个字母也做同样的操作。
现在我们想知道有多少对连线交叉。交叉的定义为一个连线的端点在另外一个连线的内部,另外一个端点在外部。
下图是一个例子,共有三对连线交叉(我们连线的时候,只能从字符串上方经过)。
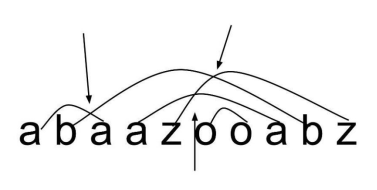
输入格式
一行一个字符串。保证字符串均由小写字母组成,且每个字母出现次数为偶数次。
输出格式
一个整数,表示答案。
样例输入
abaazooabz
样例输出
3
数据范围
对于30% 的数据,字符串长度不超过50。
对于100% 的数据,字符串长度不超过100,000。
#include <iostream> #include <cstdio> #include <algorithm> #include <cmath> #include <cstring> #include <string> using namespace std; const int N = 1e5 + 10; string s; int a[N], l[N], r[N], bel[N], last[N]; int len; long long answer; int main() { freopen("cross.in","r",stdin); freopen("cross.out","w",stdout); cin >> s; int len = s.length(); for(int i = 0; i < len; i ++) a[i + 1] = s[i] - 'a' + 1; for(int i = 1; i <= len; i ++)//yi i wei duan dian// 0 -> zuo, 1 -> you if(last[a[i]]) l[i] = last[a[i]], r[last[a[i]]] = i, last[a[i]] = 0, bel[i] = 1; else last[a[i]] = i, bel[i] = 0; for(int i = 1; i <= 26; i ++) for(int j = 1; j <= len; j ++) if(a[j] == i && bel[j] == 0){ int k = j + 1; while(a[k] != a[j]){ if(bel[k] == 1 && l[k] < j) answer ++; k ++; } j = k; } printf("%lld", answer); return 0; } /* abaazooabz 3 */
跳跳虎回家

#include <iostream> #include <cstdio> #include <algorithm> #include <cmath> #include <cstring> #include <string> #include <queue> #include <cstdlib> using namespace std; const int N = 5010; const int oo = 99999999; const int la = 2005; int n, m, q, k, now = 1; int u2[la], v2[la], w2[la]; int head[N], dis[N], dis_2[N], pre[N], is_q[N][N], cha[N]; bool vis[N]; struct Node{ int u, v, w, nxt; }; Node E[N << 2]; queue <int> Q; struct T2{ inline int read(){ int x = 0; char c = getchar(); while(c < '0' || c > '9') c = getchar(); while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar(); return x; } inline void add(int u, int v, int w){ E[now].v = v; E[now].w = w; E[now].nxt = head[u]; head[u] = now ++; return ; } inline int spfa_1(int start, int endd){ for(int i = 1; i <= n; i ++) dis[i] = oo, vis[i] = 0; dis[start] = 0; vis[start] = 1; Q.push(start); while(!Q.empty()){ int topp = Q.front(); Q.pop(); vis[topp] = 0; for(int i = head[topp]; ~ i; i = E[i].nxt){ if(dis[E[i].v] > dis[topp] + E[i].w){ dis[E[i].v] = dis[topp] + E[i].w; if(!vis[E[i].v]){ Q.push(E[i].v); vis[E[i].v] = 1; } } } } return dis[endd]; } inline int spfa_2(int start, int endd){ for(int i = 1; i <= n; i ++) dis[i] = oo, vis[i] = 0; dis[start] = 0; vis[start] = 1; Q.push(start); while(!Q.empty()){ int topp = Q.front(); Q.pop(); vis[topp] = 0; for(int i = head[topp]; ~ i; i = E[i].nxt){ if(dis[E[i].v] > dis[topp] + E[i].w && !is_q[topp][E[i].v]){ dis[E[i].v] = dis[topp] + E[i].w; if(!vis[E[i].v]){ Q.push(E[i].v); vis[E[i].v] = 1; } } } } return dis[endd]; } } t2; int main(int argc, char *argv[]){ //freopen("move.in","r",stdin); //freopen("move.out","w",stdout); n = t2.read(); m = t2.read(); q = t2.read(); k = t2.read(); for(int i = 1; i <= n; i ++) head[i] = -1; for(int i = 1; i <= m; i ++){ int u = t2.read(); int v = t2.read(); int w = t2.read(); t2.add(u, v, w); } if(k == 0){ int ans_1 = t2.spfa_1(1, n); printf("%d", ans_1 == oo ? -1 : ans_1); return 0; } for(int i = 1; i <= q; i ++){ u2[i] = t2.read(); v2[i] = t2.read(); w2[i] = t2.read(); is_q[u2[i]][v2[i]] = 1; t2.add(u2[i], v2[i], w2[i]); } if(k == 1){ int answer = oo; for(int i = 1; i <= q; i ++){ is_q[u2[i - 1]][v2[i - 1]] = 1; is_q[u2[i]][v2[i]] = 0; int now_ans = t2.spfa_2(1, n); answer = min(answer, now_ans); } printf("%d", answer); } else{ int ans_1 = t2.spfa_1(1, n); printf("%d", ans_1 == oo ? -1 : ans_1); } return 0; } /* 5 5 2 1 1 2 1 1 3 2 2 4 2 3 4 3 4 5 4 1 4 1 2 5 1 */
秀秀 和哺 噜国 ( cut )

#include<cstdio> #include<cstdlib> #define N 5555 #define M 786433 using namespace std; typedef long long LL; struct edge { int t,n; } e[N*2]; LL h[N],size[N],f[N][N],g[N],cnt[N]; int n,K,tote; void add(int u,int v) { e[++tote].t=v; e[tote].n=h[u]; h[u]=tote; return ; } void dfs(int u,int fa) { size[u]++; f[u][1]=1; for (int i=h[u]; i; i=e[i].n) { int v=e[i].t; if (v==fa) continue; dfs(v,u); for (int j=1; j<=size[u]+size[v]; j++) g[j]=0; for (int j=1; j<=size[u]; j++) g[j]=cnt[v]*f[u][j]%M; for (int j=1; j<=size[u]; j++) for (int k=1; k<=size[v]; k++) g[j+k]=(g[j+k]+f[u][j]*f[v][k]%M)%M; for (int j=1; j<=size[u]+size[v]; j++) f[u][j]=g[j]; size[u]+=size[v]; } for (int i=K; i<=size[u]; i++) cnt[u]=(cnt[u]+f[u][i])%M; return ; } int main() { scanf("%d %d",&n,&K); for (int i=1; i<n; i++) { int u,v; scanf("%d %d",&u,&v); add(u,v); add(v,u); } dfs(1,1); printf("%d\n",cnt[1]); fclose(stdin); fclose(stdout); return 0; }

