神经网络
-
什么是神经网络
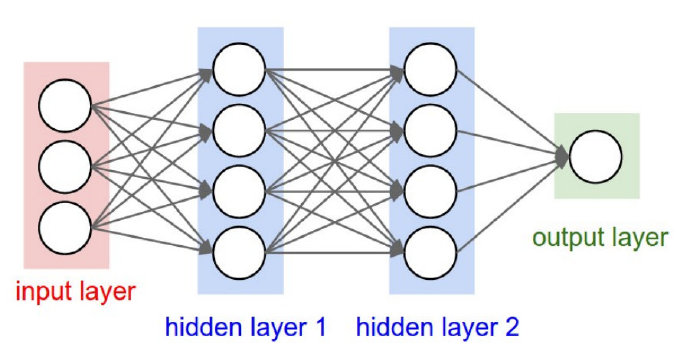
逻辑回归、感知机均只包含一个输入层以及一个输出层,只能处理线性可分问题。如果在输入层与输出层之间加入一层到多层的隐藏层,就会得到神经网络结构。
神经网络一般由输入层、隐藏层、输出层构成,下图展示了其一般结构:
隐藏层之所称之为隐藏层,是因为在训练集中,这些中间结点的准确值我们是不知道到的,也就是说你看不见它们在训练集中应具有的值。
神经网络通过在每个隐藏层后加入非线性的激活函数来使得模型具有非线性切分能力。
-
神经网络的计算过程
-
前向计算过程
对一个包含L个隐藏层(包括输入层)的神经网络,以输入层为0开始编号,则所有层的编号为\(\{0,1,...,L\}\),每个层的节点数量为\(\{n_0,n_1,...,n_L\}\)。设第\(l\)层的权重矩阵为\(W^l\in\mathbb{R}^{n_l*n_{l-1}}\),偏置矩阵为\(b^l\in\mathbb{R}^{n_l*1}\),其中\(l\in{1,2,...,L}\)。第\(l\)层未经激活的输出为\(z^l=W^la^{l-1}+b\),激活后的输出为\(a^l=act^l(z^l)\),其中\(act^l\)为第\(l\)层的激活函数。特别的,\(a^0=x\),即输入层的输出即输入。
-
反向求导过程
假设神经网络最后的损失为$ \mathcal{L}\(,反向求导过程需要计算\) \mathcal{L}\(对于所有参数的导数即\)\frac{\partial \mathcal{L}}{\partial W^l}\(和\)\frac{\partial \mathcal{L}}{\partial b^l}$,然后利用梯度下降法等方法对参数进行更新。
定义\(\delta^l=\frac{\partial \mathcal{L}}{\partial z^l} \in \mathbb{R}^{n_l*1}\),其第j个分量为\(\delta^l_j\),则根据链式求导法则有:
\[\frac{\partial \mathcal{L}}{\partial W^l_{jk}}=\frac{\partial \mathcal{L}}{\partial z^l_j}\frac{\partial z^l_j}{\partial W^l_{jk}} \\ =\delta^l_ja^{l-1}_k \\ \frac{\partial \mathcal{L}}{\partial b^l_{j}}=\frac{\partial \mathcal{L}}{\partial z^l_j}\frac{\partial z^l_j}{\partial b^l_{j}} \\ = \delta^l_j \]其中\(W^l_{jk}\)为\(W^l\)第j行第k列的元素,\(b^l_j\)为\(b^l\)的第j个分量。因此,关键是求\(\delta^l_j\)。
对于第L层,有:
\[\delta^L_j=\frac{\partial \mathcal{L}}{\partial z^L_j}=\frac{\partial \mathcal{L}}{\partial a^L_j}\frac{\partial a^L_j}{\partial z^L_j} \]记\(\frac{\partial a^l_j}{\partial z^l_j}=f’(z^l_j)\),则:
\[\delta^L_j=\frac{\partial \mathcal{L}}{\partial a^L_j}f’(z^L_j) \]对于隐藏层,由于:
\[\left\{\begin{aligned} z^{l+1}_1=\sum_jW^{l+1}_{1j}a^l_j+b^{l+1}_1 \\ z^{l+1}_2=\sum_jW^{l+1}_{2j}a^l_j+b^{l+1}_2 \\ ... \\ z^{l+1}_{n_{l+1}}=\sum_jW^{l+1}_{kj}a^l_j+b^{l+1}_{n_{l+1}} \end{aligned}\right. \]因此,使用链式法则时需要加和每个分量。则:
\[\delta^l_j=\frac{\partial \mathcal{L}}{\partial z^l_j}=(\sum_{k=1}^{n_{l+1}}\frac{\partial \mathcal{L}}{\partial z^{l+1}_k}\frac{\partial z^{l+1}_k}{\partial a^{l}_j})\frac{\partial a^{l}_j}{\partial z^{l}_j} \\ = (\sum_{k=1}^{n_{l+1}}\delta^{l+1}_jW^{l+1}_{kj})f’(z^l_j) \]将上面式子整合后写成矩阵形式即得到反向传播算法的四大公式:
\[\delta^L=\frac{\partial \mathcal{L}}{\partial z^L}=\frac{\partial \mathcal{L}}{\partial a^L}\otimes f’(z^L) \\ \delta^l=\frac{\partial \mathcal{L}}{\partial z^l}=(W^{l+1})^T\delta^{l+1}\otimes f’(z^l) \\ \frac{\partial \mathcal{L}}{\partial W^l}=\delta^l(a^{l-1})^T \\ \frac{\partial \mathcal{L}}{\partial b^l}=\delta^l \]
-
-
常用激活函数
激活函数通常具有非线性、可微性、单调性。如果激活函数是线性函数,那么再多的神经网络层仍然只能拟合线性函数。
-
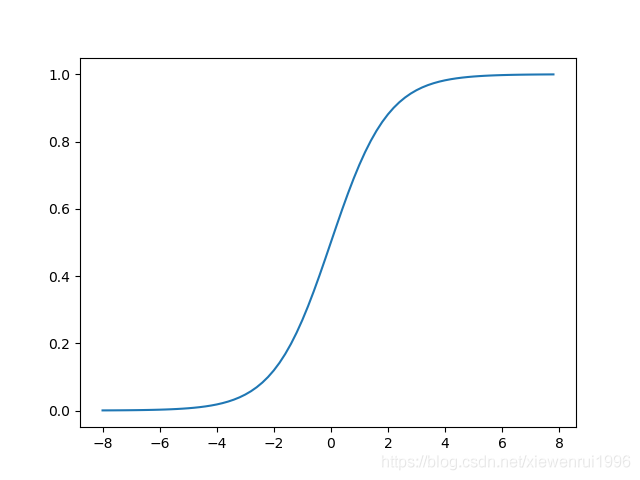
Sigmoid
函数表达式为:
\[sigmoid(z)=\frac{1}{1+e^{-z}} \in (0,1) \]![sKTuRA.png]()
导数为:
\[sigmoid'(z)=sigmoid(z)*(1-sigmoid(z)) \] -
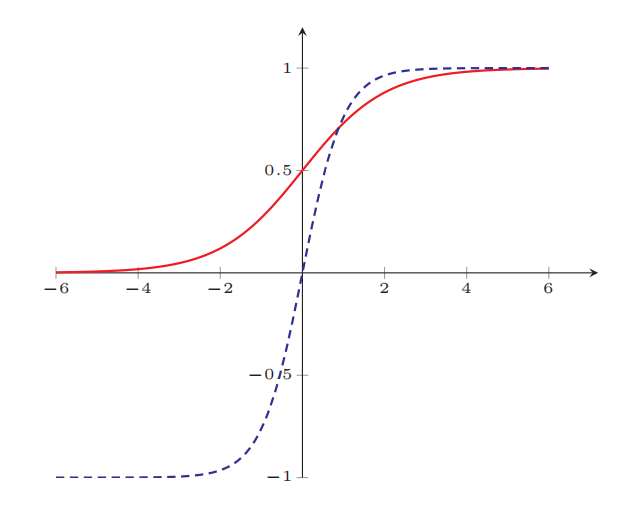
Tanh
函数表达式为:
\[tanh(z)=\frac{e^z-e^{-z}}{e^z+e^{-z}}=\frac{2}{1+e^{-2z}}-1=2sigmoid(2z)-1 \in (-1,1) \]导数为:
\[tanh'(z)=1-tanh^2(z) \] -
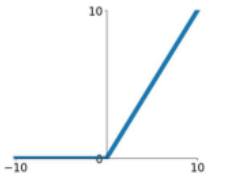
ReLU
函数表达式为:
\[relu(z)=\left\{\begin{aligned} z \qquad \quad z\ge0\\ 0 \qquad\quad z<0 \end{aligned}\right. \]导数为:
\[relu'(z)=\left\{\begin{aligned} 1 \qquad \quad z\ge0\\ 0 \qquad\quad z<0 \end{aligned}\right. \] -
Softmax
函数表达式为:
\[softmax(z_i)=\frac{e^{z_i}}{\sum_ie^{z_i}}=a_i \]与上述几个激活函数不同,Softmax输入和输出都为一个向量,目的是对输入向量进行概率归一化。
当\(i=j\)时,导数为:
\[\frac{\partial softmax(z_i)}{\partial z_j}=\frac{\partial}{\partial z_j}\frac{e^{z_i}}{\sum_ie^{z_i}} \\ = \frac{e^{z_i}\sum_ie^{z_i}-e^{z_i}e^{z_j}}{(\sum_ie^{z_i})^2} \\ = a_i-a_ia_j \]当\(i\neq j\)时,导数为:
\[\frac{\partial softmax(z_i)}{\partial z_j}=\frac{\partial}{\partial z_j}\frac{e^{z_i}}{\sum_ie^{z_i}} \\ = \frac{-e^{z_i}e^{z_j}}{(\sum_ie^{z_i})^2} \\ = -a_ia_j \]Softmax将逻辑回归由二分类推广到多分类。
-
常用激活函数比较
Sigmod和Tanh函数的导数在正负饱和区都趋近于0,很容易造成梯度消失现象,而ReLU函数的导数大于 0 部分都为常数,不会产生梯度消失现象。但ReLU函数进入负半区的时候,梯度为 0,对应神经元此时不会被训练,这在一定程度上可以环节过拟合,但也有可能产生神经元坏死的问题,即一旦神经元变为负数,它就不太可能恢复。因此产生了Leaky ReLU激活函数,在负半区仍具有很小的梯度。
ReLU激活函数的优势还体现在它的计算速度上,用一个简单的if-else就可以实现,大大节省了计算时间。
-
-
参数初始化方法
神经网络通常需要随机初始化参数,并且将参数初始化得很小。
如果将每个隐藏单元的参数都初始化为相等的值,那么在正向传播时每个隐藏单元将根据相同的输⼊计算出相同的值, 并传递⾄输出层。在反向传播中,每个隐藏单元的参数梯度值相等。因此,这些参数在使⽤基于梯度的优化算法迭代后值依然相等。之后的迭代也是如此。在这种情况下,⽆论隐藏单元有多少, 隐藏层本质上只有1个隐藏单元在发挥作⽤。
将参数初始化得很小能够避免出现梯度爆炸的现象。梯度消失与梯度爆炸在后面会详细介绍。
常用的两种初始化方法为:
-
采用正态分布的随机初始化方法。
-
Xavier初始化方法:假设某全连接层的输入个数为a,输出个数为b,Xavier随机初始化将使该层中权重参数的每个元素都随机采样于均匀分布:
\[U(-\sqrt{\frac{6}{a+b}},\sqrt{\frac{6}{a+b}}) \]初始化后,每层输出的方差不会受该层输入个数的影响,且每层梯度的方差也不受该层输出个数的影响。
-
-
交叉熵损失函数
交叉熵损失函数为最常用的分类损失函数,其表达式为:
\[\mathcal{L}(y,a)=-\sum_{j}y_j\log a_j \]其中\(y_j\)为类别j的真实标签,\(a_j\)为类别j的预测概率值。对于多分类问题,只有一个类别对应的\(y_j\)为1,其余均为0,因此:
\[\mathcal{L}(y,a)=-\log a_i \]其中i为样本的真实类别。
输出层通常选用Softmax或者Sigmoid作为激活函数,下面分别讨论二者的反向求导过程,即如何求前面所说的\(\delta^L\)。
-
交叉熵+Softmax
设样本的真实类别为i,当\(i=j\)时,导数为:
\[\frac{\partial \mathcal{L}}{\partial z^L_j}=-\frac{1}{a_i}(a_i-a_ia_j)=a_j-1=a_j-y_j \]当\(i\neq j\)时,导数为:
\[\frac{\partial \mathcal{L}}{\partial z^L_j}=-\frac{1}{a_i}(-a_ia_j)=a_j==a_j-y_j \]因此:
\[\frac{\partial \mathcal{L}}{\partial z^L}=a^L-y \] -
交叉熵+Sigmoid
当\(i=j\)时,导数为:
\[\frac{\partial \mathcal{L}}{\partial z^L_j}=-\frac{1}{a_i}a_j(1-a_j)=a_j-1=a_j-y_j \]当\(i\neq j\)时,导数为:
\[\frac{\partial \mathcal{L}}{\partial z^L_j}=0 \]因此:
\[\frac{\partial \mathcal{L}}{\partial z^L}=(a^L-y)\otimes y \]
-
-
梯度消失与梯度爆炸
为了简化问题,假设神经网络的输入以及所有层都只有一个结点并且没有偏置项,那么根据前面得出的反向传播求导公式,有:
\[\frac{\partial \mathcal{L}}{\partial W^l}=a^{l-1}W^{l+1}f’(z^l)W^{l+2}f’(z^{l+1})...W^{L}f’(z^{L-1})\frac{\partial \mathcal{L}}{\partial z^L} \]当激活函数选用Sigmoid或者Tanh时,若输入位于正负饱和区,\(f'\)会变得非常小,很多个非常小的数相乘会导致结果趋于0,使得接近输入层的所有层的梯度趋于0,权重和偏差参数无法被更新,导致神经网络无法被优化,训练永远不会收敛到良好的解决方案。 这被称为梯度消失问题。解决方案为选用ReLU等非饱和的激活函数等。
若参数W初始化得很大,那么多个大于1的数相乘会使得结果很大,使得接近输入层的所有层的梯度非常大,权重和偏差参数的更新量非常大,无法被正确更新。这被称为梯度爆炸问题。解决方案为将参数初始化的很小、进行梯度截断等。
-
优化方法
-
随机梯度下降(SGD):
由于负梯度方向为函数下降最快的方向,因此梯度下降法使用迭代的方法,每次朝负梯度方向移动一个很小的距离\(\alpha\)(学习率)。通过不断迭代直到到达损失函数的全局最小点或者局部最小点。
由于显存等计算资源的限制,每次仅在一个较小的mini-batch上对参数进行更新。对于每一个mini-batch,通过前面得出的反向传播求导公式计算每个样本的\(\frac{\partial \mathcal{L}}{\partial W^l}\)和\(\frac{\partial \mathcal{L}}{\partial b^l}\),然后对计算结果取均值得到\(\Delta w\)以及\(\Delta b\)。使用下式对参数进行更新:
\[w=w-\alpha\Delta w \\ b=b-\alpha\Delta b \]Batch_Size 对训练效果的影响:
- Batch_Size 太小,很多时刻优化方向都可能是远离最小点方向,因此模型表现效果极其糟糕(error飙升)。
- 随着 Batch_Size 增大,处理相同数据量的速度越快。
- 随着 Batch_Size 增大,达到相同精度所需要的 epoch 数量越来越多。
- 由于上述两种因素的矛盾, Batch_Size 增大到某个时候,达到时间上的最优。
- 由于最终收敛精度会陷入不同的局部极值,因此 Batch_Size 增大到某些时候,达到最终收敛精度上的最优。
-
Adam等方法之后逐步添加。
-
-
过拟合处理方法
-
Dropout
在训练的前向传播过程中,通过让某个神经元的激活值以一定的概率p停止工作,从而降低过拟合。
Dropout降低过拟合的原理:
- 由于Dropout的随机失活性,使得训练过程中会产生不同的子网络,测试的时候相当于对这些子网络进行集成,能够更好的降低过拟合。
- Dropout导致两个神经元不一定每次都在同一个子网络中出现,这样权值的更新不再依赖于有固定关系的隐含节点的共同作用,阻止了某些特征仅仅在其它特定特征下才有效果的情况 。迫使网络去学习更加鲁棒的特征 ,这些特征在其它的神经元的随机子集中也存在。
为了保证训练和测试时每一层输出的期望值相同,若在训练时以概率p失活,那么在测试时需要对输出乘以(1-p),或者在训练时除以(1-p)。
-
L2正则化
在原有损失函数的基础上加上L2正则化项\(\lambda\sum w^2\)即结构风险,用来控制模型的复杂度,从而降低过拟合。
-
-
Batch Normalization(批规范化)
对于深度学习这种包含很多隐层的网络结构,在训练过程中,因为各层参数老在变,所以每个隐层都会面临covariate shift的问题,也就是在训练过程中,隐层的输入分布老是变来变去,这就是所谓的“Internal Covariate Shift”,Internal指的是深层网络的隐层,是发生在网络内部的事情,而不是covariate shift问题只发生在输入层。
BN的基本思想其实相当直观:因为深层神经网络在做非线性变换前的激活输入值(z)随着网络深度加深或者在训练过程中,其分布逐渐发生偏移或者变动,之所以训练收敛慢,一般是整体分布逐渐往非线性函数的取值区间的上下限两端(正负饱和区)靠近,容易导致梯度消失,这是训练深层神经网络收敛越来越慢的本质原因。而Batch Normalization就是通过一定的规范化手段,把每层神经网络任意神经元这个输入值的分布强行拉回到均值为0方差为1的标准正态分布。
BN流程如下:
在训练的过程中,BN通过在每一个Mini-Batch里面将激活函数输入值减去Mini-Batch内数据的均值除以Mini-Batch内数据的方差进行标准化。
需要注意的是,这里多出的scale and shift操作是为了让因训练所需而“刻意”加入的BN能够有可能还原最初的输入(scale and shift的参数是可学习的),从而保证整个network的capacity。(有关capacity的解释:实际上BN可以看作是在原模型上加入的新操作,这个新操作很大可能会改变某层原来的输入。当然也可能不改变,不改变的时候就是还原原来输入。如此一来,既可以改变同时也可以保持原输入,那么模型的容纳能力(capacity)就提升了。)
BN在推理时使用的均值和方差为所有mini-batches训练样本均值和方差的累计滑动平均结果。
BN的好处:
- 加快模型收敛,缩短训练时间;
- 防止梯度消失。
BN一般用在激活函数前,但也有用在激活函数后的,需要通过实验来验证。
AI基础知识与代码实现:github


 浙公网安备 33010602011771号
浙公网安备 33010602011771号