EM算法

1. 什么是EM算法

   EM算法用于含有隐变量的概率模型参数的极大似然估计，或极大后验概率估计。

   EM算法详细过程：

   输入：观测变量数据Y，隐变量数据Z，联合分布\(P(Y,Z|\theta)\)，条件分布\(P(Z|Y,\theta)\)；

   输出：模型参数\(\theta\).

   1. 选择参数的初值\(\theta^{(0)}\)，开始迭代；

   2. E步：记\(\theta^{(i)}\)为第i次迭代参数\(\theta\)的估计值，在第i+1次迭代的E步，计算Q函数：

      \[Q(\theta,\theta^{(i)})=E_Z(\log P(Y,Z|\theta)|Y,\theta^{(i)}) \\=\sum_{Z}P(Z|Y,\theta^{(i)})\log P(Y,Z|\theta) \]

      这里，\(P(Z|Y,\theta^{(i)})\)是给定观测数据以及当前参数估计下隐变量Z的条件概率分布；

   3. M步：求

      \[\theta^{(i+1)}=\arg \max_{\theta}Q(\theta,\theta^{(i)}) \]

   4. 重复2、3步直到收敛。

   EM算法的几点说明：

   1. Q函数是完全数据的对数似然函数\(\log P(Y,Z|\theta)\)关于在给定观测数据Y和当前的参数\(\theta^{(i)}\)下对未观测数据Z的条件概率分布\(P(Z|Y,\theta^{(i)})\)的期望。

   2. 参数初值可以任意选取，但EM算法是对初值敏感的，一般做法是选取几个不同的初值进行迭代，然后对得到的各个估计值进行比较，从中选择最好的。

   3. 迭代停止的条件一般是对较小的正数\(\varepsilon_1,\varepsilon_2\)，满足：

      \[||\theta^{(i+1)}-\theta^{(i)}||<\varepsilon_1或||Q(\theta^{(i+1)},\theta^{(i)})-Q(\theta^{(i)},\theta^{(i)})||<\varepsilon_2 \]

2. EM的导出

   我们面对一个含有隐变量的概率模型，目标是极大化观测数据Y关于参数\(\theta\)的对数似然函数，即极大化：

   \[L(\theta)=\log P(Y|\theta)=\log\sum_{Z}P(Y,Z|\theta) \\=\log\sum_{Z}P(Y|Z,\theta)P(Z|\theta) \]

   上式中既包含未观测变量并且还包含和的对数，难以求解。

   EM算法的思想是通过迭代逐步极大化\(L(\theta)\)。假设在第i次迭代之后参数的估计值为\(\theta^{(i)}\)，我们希望新的估计值\(\theta\)能使\(L(\theta)\)增加，即\(L(\theta)>L(\theta^{(i)})\)，为此考虑二者的差：

   \[L(\theta)-L(\theta^{(i)})=\log\sum_{Z}P(Y|Z,\theta)P(Z|\theta)-\log P(Y|\theta^{(i)}) \\=\log\frac{\sum_{Z}P(Y|Z,\theta)P(Z|\theta)}{P(Y|\theta^{(i)})} \\=\log\sum_{Z}\frac{P(Y|Z,\theta)P(Z|\theta)}{P(Y|\theta^{(i)})} \\=\log\sum_{Z}\frac{P(Y|Z,\theta)P(Z|\theta)}{P(Y|\theta^{(i)})P(Z|Y,\theta^{(i)})}P(Z|Y,\theta^{(i)}) \\\ge\sum_{Z}P(Z|Y,\theta^{(i)})\log\frac{P(Y|Z,\theta)P(Z|\theta)}{P(Y|\theta^{(i)})P(Z|Y,\theta^{(i)})}\qquad(琴生不等式) \]

   令：

   \[B(\theta,\theta^{(i)})=L(\theta^{(i)})+\sum_{Z}P(Z|Y,\theta^{(i)})\log\frac{P(Y|Z,\theta)P(Z|\theta)}{P(Y|\theta^{(i)})P(Z|Y,\theta^{(i)})} \]

   则：

   \[L(\theta)\ge B(\theta,\theta^{(i)}) \]

   且：

   \[L(\theta^{(i)})=B(\theta,\theta^{(i)}) \]

   因此，\(B(\theta,\theta^{(i)})\)是\(L(\theta)\)的一个下界。为了使\(L(\theta)\)有尽可能大的增大，选择\(\theta^{(i+1)}\)使得\(B(\theta,\theta^{(i)})\)达到极大，即：

   \[\theta^{(i+1)}=\arg \max_{\theta}B(\theta,\theta^{(i)}) \]

   现在求上式，省去对\(\theta\)极大化而言是常数的项：

   \[\theta^{(i+1)}=\arg \max_{\theta}B(\theta,\theta^{(i)})=\arg \max_{\theta}(L(\theta^{(i)})+\sum_{Z}P(Z|Y,\theta^{(i)})\log\frac{P(Y|Z,\theta)P(Z|\theta)}{P(Y|\theta^{(i)})P(Z|Y,\theta^{(i)})}) \\=\arg \max_{\theta}(\sum_{Z}P(Z|Y,\theta^{(i)})\log P(Y|Z,\theta)P(Z|\theta)) \\=\arg \max_{\theta}Q(\theta,\theta^{(i)}) \]

   上式等价于EM算法的一次迭代，因此EM算法是通过不断求解观测数据Y关于参数\(\theta\)的对数似然函数的下界的极大化来进行参数估计的。

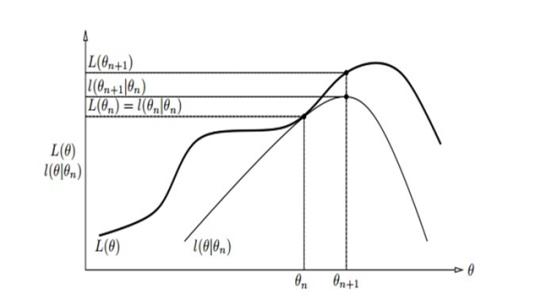
   下图给出了EM算法的直观解释：

   

   下方曲线为\(B(\theta,\theta^{(i)})\)，上方曲线为\(L(\theta)\)。

3. EM算法的收敛性

   • 设\(P(Y|\theta)\)为观测数据的似然函数，\(\theta^{(i)},i=1,2,...\)是EM算法得到的参数估计序列，\(P(Y|\theta^{(i)})\)为对应的似然函数序列，则\(P(Y|\theta^{(i)})\)是单调递增的，即：

     \[P(Y|\theta^{(i+1)})\ge P(Y|\theta^{(i)}) \]

     证明过程如下：

     \[\log P(Y|\theta)=\log \frac{P(Y,Z|\theta)}{P(Z|Y,\theta)}=\log P(Y,Z|\theta)-\log P(Z|Y,\theta) \]

     在给定观测数据Y和第i轮参数\(\theta^{(i)}\)的情况下：

     \[\log P(Y|\theta)=\sum_{Z}P(Z|Y,\theta^{(i)})(\log P(Y,Z|\theta)-\log P(Z|Y,\theta)) \\=\sum_{Z}P(Z|Y,\theta^{(i)})\log P(Y,Z|\theta)-P(Z|Y,\theta^{(i)})\log P(Z|Y,\theta) \\=Q(\theta,\theta^{(i)})-P(Z|Y,\theta^{(i)})\log P(Z|Y,\theta) \]

     令：

     \[H(\theta,\theta^{(i)})=P(Z|Y,\theta^{(i)})\log P(Z|Y,\theta) \]

     则：

     \[\log P(Y|\theta)=Q(\theta,\theta^{(i)})-H(\theta,\theta^{(i)}) \]

     则：

     \[\log P(Y|\theta^{(i+1)})-\log P(Y|\theta^{(i)})=(Q(\theta^{(i+1)},\theta^{(i)})-H(\theta^{(i+1)},\theta^{(i)}))-(Q(\theta^{(i)},\theta^{(i)})-H(\theta^{(i)},\theta^{(i)})) \\=(Q(\theta^{(i+1)},\theta^{(i)})-Q(\theta^{(i)},\theta^{(i)}))-(H(\theta^{(i+1)},\theta^{(i)})-H(\theta^{(i)},\theta^{(i)})) \]

     由于\(\theta^{(i+1)}\)使得\(Q(\theta,\theta^{(i)})\)取得极大，因此：

     \[Q(\theta^{(i+1)},\theta^{(i)})-Q(\theta^{(i)},\theta^{(i)})\ge 0 \]

     而：

     \[H(\theta^{(i+1)},\theta^{(i)})-H(\theta^{(i)},\theta^{(i)})=\sum_{Z}(P(Z|Y,\theta^{(i)})\log \frac{P(Z|Y,\theta^{(i+1)})}{P(Z|Y,\theta^{(i)})}) \\\le\log (\sum_{Z}P(Z|Y,\theta^{(i)})\frac{P(Z|Y,\theta^{(i+1)})}{P(Z|Y,\theta^{(i)})}))\qquad(琴生不等式) \\=\log \sum_{Z}P(Z|Y,\theta^{(i+1)}) =0 \]

     因此：

     \[-H(\theta^{(i)},\theta^{(i)}))\ge0 \]

     因此：

     \[\log P(Y|\theta^{(i+1)})-\log P(Y|\theta^{(i)})\ge0 \]

     个人觉得其实证明过程没必要这么复杂，由前面EM算法的导出有：

     \[L(\theta^{(i+1)})\ge B(\theta^{(i+1)},\theta^{(i)})\ge B(\theta^{(i)},\theta^{(i)})=L(\theta^{(i)}) \]

     即：

     \[\log P(Y|\theta^{(i+1)})\ge \log P(Y|\theta^{(i)}) \]

   • 如果\(P(Y|\theta)\)有上界，则\(L(\theta^{(i)})=\log P(Y|\theta^{(i)})\)收敛到某一值。（单调有界收敛准则）

   • 在Q函数与\(L(\theta)\)满足一定条件下，EM算法得到的参数估计序列的收敛值是\(L(\theta)\)的稳定点。

4. EM算法在三硬币模型中的应用

   • 三硬币模型

     假设有3枚硬币，分别记作A，B，C。这些硬币正面朝上的概率分别为\(\pi,p,q\)。进行如下掷硬币的实验：先掷硬币A，根据其结果选出硬币B或C，正面选B，反面选C；然后掷选出的硬币，掷硬币的结果正面记作1，反面记作0；独立地重复实验n次，假设只能观测到掷硬币的结果，不能观测掷硬币的过程，问如何估计\(\pi,p,q\)。

   • 将观测数据记作\(Y=(y_1,y_2,...,y_n)\)，未观测到的数据（硬币A的朝向）记作\(Z=(z_1,z_2,...,z_n)\)，使用EM算法求解参数。设第i次迭代的参数为\(\theta^{(i)}=(\pi^{(i)},p^{(i)},q^{(i)})\)，则Q函数为：

     \[Q(\theta,\theta^{(i)})=E_Z(\log P(Y,Z|\theta)|Y,\theta^{(i)}) \\=\sum_{Z}P(Z|Y,\theta^{(i)})\log P(Y,Z|\theta) \\=\sum_{Z}\prod_{j=1}^nP(z_j|y_j,\theta^{(i)})\log \prod_{j=1}^nP(z_j,y_j|\theta) \\=\sum_{Z}\prod_{j=1}^nP(z_j|y_j,\theta^{(i)})\sum_{j=1}^n\log P(z_j,y_j|\theta) \\=\sum_{Z}(\prod_{j=1}^nP(z_j|y_j,\theta^{(i)})\log P(z_1,y_1|\theta)+\prod_{j=1}^nP(z_j|y_j,\theta^{(i)})\sum_{j=2}^n\log P(z_j,y_j|\theta)) \]

     由于：

     \[\sum_{Z}(\prod_{j=1}^nP(z_j|y_j,\theta^{(i)})\log P(z_1,y_1|\theta) \\=\sum_{z_1,z_2,...,z_n}(P(z_1|y_1,\theta^{(i)})\prod_{j=2}^nP(z_j|y_j,\theta^{(i)})\log P(z_1,y_1|\theta) \\=P(z_1=1|y_1,\theta^{(i)})\log P(z_1=1,y_1|\theta)\sum_{z_2,...,z_n}\prod_{j=2}^nP(z_j|y_j,\theta^{(i)})\\+P(z_1=0|y_1,\theta^{(i)})\log P(z_1=0,y_1|\theta)\sum_{z_2,...,z_n}\prod_{j=2}^nP(z_j|y_j,\theta^{(i)}) \\=\sum_{z_1}P(z_1|y_1,\theta^{(i)})\log P(z_1,y_1|\theta)\sum_{z_2,...,z_n}\prod_{j=2}^nP(z_j|y_j,\theta^{(i)}) \]

     由于：

     \[\sum_{z_2,...,z_n}\prod_{j=2}^nP(z_j|y_j,\theta^{(i)}) \\=\sum_{z_2,...,z_n}P(z_2|y_2,\theta^{(i)})\prod_{j=3}^nP(z_j|y_j,\theta^{(i)}) \\=\sum_{z_2}P(z_2|y_2,\theta^{(i)})\sum_{z_3,...,z_n}\prod_{j=3}^nP(z_j|y_j,\theta^{(i)}) \\=\sum_{z_3,...,z_n}\prod_{j=3}^nP(z_j|y_j,\theta^{(i)}) \\=...=1 \]

     所以：

     \[\sum_{Z}(\prod_{j=1}^nP(z_j|y_j,\theta^{(i)})\log P(z_1,y_1|\theta) \\=\sum_{z_1}P(z_1|y_1,\theta^{(i)})\log P(z_1,y_1|\theta) \]

     由于：

     \[\sum_{Z}(\prod_{j=1}^nP(z_j|y_j,\theta^{(i)})\sum_{j=2}^n\log P(z_j,y_j|\theta)) \\=\sum_{z_1,z_2,...,z_n}(P(z_1|y_1,\theta^{(i)})\prod_{j=2}^nP(z_j|y_j,\theta^{(i)})\sum_{j=2}^n\log P(z_j,y_j|\theta)) \\=\sum_{z_1}P(z_1|y_1,\theta^{(i)})\sum_{z_2,...,z_n}(\prod_{j=2}^nP(z_j|y_j,\theta^{(i)})\sum_{j=2}^n\log P(z_j,y_j|\theta)) \\=\sum_{z_2,...,z_n}(\prod_{j=2}^nP(z_j|y_j,\theta^{(i)})\sum_{j=2}^n\log P(z_j,y_j|\theta)) \]

     所以：

     \[Q(\theta,\theta^{(i)})=\sum_{z_1}P(z_1|y_1,\theta^{(i)})\log P(z_1,y_1|\theta)+\sum_{z_2,...,z_n}(\prod_{j=2}^nP(z_j|y_j,\theta^{(i)})\sum_{j=2}^n\log P(z_j,y_j|\theta)) \\=\sum_{z_1}P(z_1|y_1,\theta^{(i)})\log P(z_1,y_1|\theta)+\sum_{z_2}P(z_2|y_2,\theta)\log P(z_2,y_2|\theta)+... \\=\sum_{j=1}^n\sum_{z_j}(P(z_j|y_j,\theta^{(i)})\log P(z_j,y_j|\theta)) \\=\sum_{j=1}^n(P(z_j=1|y_j,\theta^{(i)})\log P(z_j=1,y_j|\theta)+P(z_j=0|y_j,\theta^{(i)})\log P(z_j=0,y_j|\theta)) \]

     由于：

     \[P(z_j=1|y_j,\theta^{(i)})=\frac{P(z_j=1,y_j|\theta^{(i)})}{P(y_j|\theta^{(i)})} \\=\frac{P(z_j=1|\theta^{(i)})P(y_j|z_j=1,\theta^{(i)})}{P(z_j=1|\theta^{(i)})P(y_j|z_j=1,\theta^{(i)})+P(z_j=0|\theta^{(i)})P(y_j|z_j=0,\theta^{(i)})} \\=\frac{\pi^i p^{(i)y}_j(1-p^i)^{1-y_j}}{\pi^i p^{(i)y}_j(1-p^i)^{1-y_j}+(1-\pi^i) q^{(i)y}_j(1-q^i)^{1-y_j}} \\=\mu_j^i \\ P(z_j=0|y_j,\theta^{(i)})=1-\mu_j^i \\ P(z_j=1,y_j|\theta)=P(z_j=1|\theta)P(y_j|z_j=1,\theta)=\pi p^y_j(1-p)^{1-y_j} \\ P(z_j=0,y_j|\theta)=P(z_j=0|\theta)P(y_j|z_j=0,\theta)=(1-\pi) q^y_j(1-q)^{1-y_j} \]

     所以：

     \[Q(\theta,\theta^{(i)})=\sum_{j=1}^n(\mu_j^i\log \pi p^y_j(1-p)^{1-y_j}+(1-\mu_j^i)\log (1-\pi) q^y_j(1-q)^{1-y_j}) \]

     分别对\(\pi,p,q\)求导并令其等于0，求得：

     \[\pi=\frac{1}{n}\sum_{j=1}^n\mu_j^i \\p=\frac{\sum_{j=1}^n\mu_j^iy_j}{\sum_{j=1}^n\mu_j^i} \\q=\frac{\sum_{j=1}^n(1-\mu_j^i)y_j}{\sum_{j=1}^n(1-\mu_j^i)} \]

5. EM算法在高斯混合模型中的应用

   • 高斯混合模型

     高斯混合模型是指具有如下形式的概率分布模型：

     \[p(y|\theta)=\sum_{k=1}^K\alpha_k\phi(y|\theta_k) \]

     其中，\(\alpha_k\ge 0\)是系数，\(\sum_{k=1}^K\alpha_k=1\)。\(\phi(y|\theta_k)\)是高斯分布密度，\(\theta_k=(\mu_k,\sigma_k^2)\)，

     \[\phi(y|\theta_k)=\frac{1}{\sqrt {2\pi}\sigma_k}e^{-\frac{(y-\mu_k)^2}{2\sigma_k^2}} \]

     称为第k个分模型。

     假设观测数据\(Y=(y_1,y_2,...,y_n)\)由以上高斯混合模型生成，其中\(\theta=(\alpha_1,\alpha_2,...,\alpha_K;\theta_1,\theta_2,...,\theta_K)\)，我们用EM算法来进行参数估计。

   • 可以设想观测数据\(y_j\)是这样产生的：首先依概率\(\alpha_k\)选择第k个高斯分布，然后依第k个分模型的参数生成观测数据。以隐变量\(\gamma_{jk}=1\)表示第j个观测来自第j个模型，否则为0。于是EM算法的观测数据为\(Y=(y_1,y_2,...,y_n)\)，未观测数据为\(\gamma=(\gamma_{j1},\gamma_{j2},...,\gamma_{jK}),j=1,2,...,n\)。

     完全数据的对数似然函数为：

     \[P(Y,\gamma|\theta)=\prod_{j=1}^n\prod_{k=1}^K(\alpha_k\phi(y|\theta_k))^{\gamma_{jk}} \\=\prod_{j=1}^n\prod_{k=1}^K(\alpha_k\frac{1}{\sqrt {2\pi}\sigma_k}e^{-\frac{(y-\mu_k)^2}{2\sigma_k^2}})^{\gamma_{jk}} \]

     完全数据的对数似然函数为：

     \[\log P(Y,\gamma|\theta)=\sum_{j=1}^n\sum_{k=1}^K\gamma_{jk}\log(\alpha_k\frac{1}{\sqrt {2\pi}\sigma_k}e^{-\frac{(y-\mu_k)^2}{2\sigma_k^2}}) \\=\sum_{j=1}^n\sum_{k=1}^K\gamma_{jk}(\log \alpha_k-\log \sqrt {2\pi}\sigma_k-\frac{(y-\mu_k)^2}{2\sigma_k^2}) \]

     则Q函数为：

     \[Q(\theta,\theta^{(i)})=E(\log P(Y,\gamma|\theta)|Y,\theta^{(i)}) \\=E(\sum_{j=1}^n\sum_{k=1}^K\gamma_{jk}(\log \alpha_k-\log \sqrt {2\pi}\sigma_k-\frac{(y-\mu_k)^2}{2\sigma_k^2})) \\=\sum_{j=1}^n\sum_{k=1}^KE(\gamma_{jk})(\log \alpha_k-\log \sqrt {2\pi}\sigma_k-\frac{(y-\mu_k)^2}{2\sigma_k^2}) \]

     由于：

     \[E(\gamma_{jk})=P(\gamma_{jk}=1|Y,\theta^{(i)}) \\=P(\gamma_{jk}=1|y_j,\theta^{(i)}) \\=\frac{P(\gamma_{jk}=1,y_j|\theta^{(i)})}{P(y_j|\theta^{(i)})} \\=\frac{P(\gamma_{jk}=1|\theta^{(i)})P(y_j|\gamma_{jk}=1,\theta^{(i)})}{\sum_{k=1}^KP(\gamma_{jk}=1|\theta^{(i)})P(y_j|\gamma_{jk}=1,\theta^{(i)})} \\=\frac{\alpha_k^i\phi(y_j|\theta_k^i)}{\sum_{k=1}^K\alpha_k^i\phi(y_j|\theta_k^i)} \\=\hat\gamma_{jk}^i \]

     所以：

     \[Q(\theta,\theta^{(i)})=\sum_{j=1}^n\sum_{k=1}^K\hat\gamma_{jk}^i(\log \alpha_k-\log \sqrt {2\pi}\sigma_k-\frac{(y-\mu_k)^2}{2\sigma_k^2}) \]

     分别对\(\mu_k,\sigma_k\)求导并令其等于0，求得：

     \[\mu_k^{(i+1)}=\frac{\sum_{j=1}^n\hat\gamma_{jk}^iy_j}{\sum_{j=1}^n\hat\gamma_{jk}^i} \\\sigma_k^{2,(i+1)}=\frac{\sum_{j=1}^n\hat\gamma_{jk}^i(y_j-\mu_k^{(i+1)})^2}{\sum_{j=1}^n\hat\gamma_{jk}^i} \]

     求\(\alpha_k\)需要利用约束条件\(\sum_{k=1}^K\alpha_k=1\)，使用拉格朗日乘子法求解，最终求得：

     \[\alpha_K^{(i+1)}=\frac{\sum_{j=1}^n\hat\gamma_{jk}^i}{n} \]