逻辑回归
-
什么是逻辑回归？
逻辑回归一般指二项逻辑回归，是一种用于二分类的判别式模型。
设输入样本为\(x\in\mathbb{R}^n\)，样本标签\(y\in\{0,1\}\)逻辑回归的参数为：\(w\in\mathbb{R}^n, b\in\mathbb{R}\)，逻辑回归按照下式得到样本属于标签1的概率：
\[p=\frac{1}{1+e^{-(w^Tx+b)}} \]称函数\(\sigma(z)=\frac{1}{1+e^{-z}}\)为sigmoid函数，则：
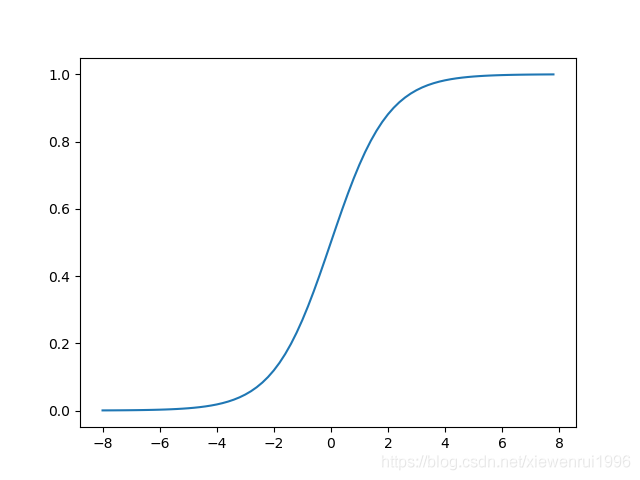
\[p=\sigma(w^Tx+b) \]sigmoid函数图像为：
当输入为0时输出为0.5，当输入分别趋向正无穷和负无穷时，输出分别趋向1和0。
一个事件的几率是指该事件发生的概率与其不发生的概率的比值，该事件的对数几率是：
\[logit(p)=\ln \frac{p}{1-p} \]将逻辑回归的表达式带入上式得：
\[logit(p)=\ln \frac{\frac{1}{1+e^{-(w^Tx+b)}}}{\frac{e^{-(w^Tx+b)}}{1+e^{-(w^Tx+b)}}}=w^Tx+b \]可以看出，输出y=1的对数几率是输入x的线性组合，即逻辑回归实际上是在对对数几率进行回归，这也是逻辑回归名称的由来。
-
逻辑回归损失函数
设训练集大小为N，则逻辑回归的对数似然函数为：
\[\ln L(w,b)=\ln \prod_{i=1}^Np_i^{y_i}(1-p_i)^{1-y_i}=\sum_{i=1}^N(y_i\ln p_i + (1-y_i)\ln (1-p_i)) \\=\sum_{i=1}^N(y_i\ln \frac{p_i}{1-p_i}+\ln (1-p_i))=\sum_{i=1}^N(y_i(w^Tx_i+b)-\ln (1+e^{w^Tx_i+b})) \]使用负对数似然函数的均值作为损失函数，即：
\[Loss(w,b)=-\frac{1}{N}\ln L(w,b) \]对w和b求偏导得：
\[\frac{\partial Loss(w,b)}{\partial w}=\frac{1}{N}\sum_{i=1}^Nx_i(p_i-y_i) \\ \frac{\partial Loss(w,b)}{\partial b}=\frac{1}{N}\sum_{i=1}^N(p_i-y_i) \]也可以令\(z_i=w^Tx_i+b\)，通过以下方法进行链式求导：
\[\frac{\partial Loss(w,b)}{\partial w}=\sum_{i=1}^N\frac{\partial Loss(w,b)}{\partial p_i}\frac{\partial p_i}{\partial z_i}\frac{\partial z_i}{\partial w} \]由于sigmoid函数存在以下性质：
\[\frac{\partial \sigma(z)}{\partial z}=\sigma(z)(1-\sigma(z)) \]所以链式求导也很容易。两种方式结果相同。
