数论学习(2019.4.4 - 2019.4.7) --4.5
今天钟长者讲课吖qqqq
一、质数
有一个定理: 设p为质数,若p | ab ,则 p | a或者p | b;
二、整数唯一分解定理

这个证明是用的反证法:
1.存在性
设立N为不满足条件的最小的数
若N为质数 显然不成立
若N为合数 由于N = an 则n也不能分解 因此不成立
2.唯一性
设N为不可以被整除的最小的数
若N为质数 因为N = N^1 显然不成立
若N为合数 N = P * N / P 因为N为最小的,而 N / P却更小,因此不成立
证毕
三、Miller_Rabin素性测试
如果N为素数,取a < n;
设n - 1 = d * 2 ^ r
则下列两个结论中必定满足一个:
1.
2.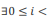
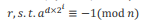
先贴代码吧:
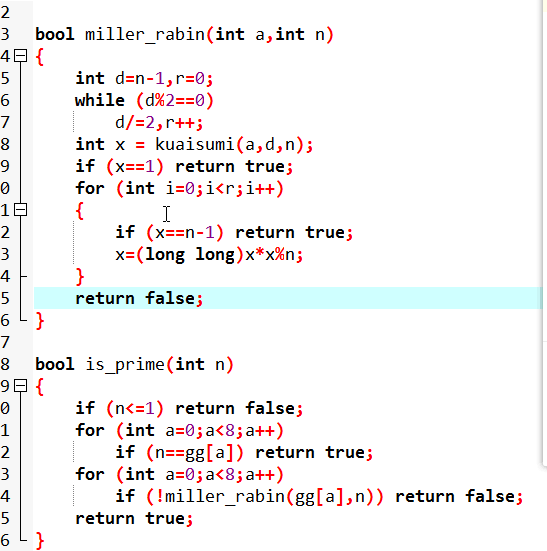
其中定义的gg[]数组就是8个素数
证明:
我们使用平方差公式,运用欧拉定理进行证明:
(手写qwq)

(像素好低啊q)
三、筛法
埃氏筛,欧拉筛昨天讲了,代码也放在昨天了,今天就不再提起了
四、最大公因数
欧几里得算法的核心思想:
gcd(a,b) = gcd(b,a - b)
推导得出: gcd(a,b) = gcd(a,a % b)
证明:
反证法:
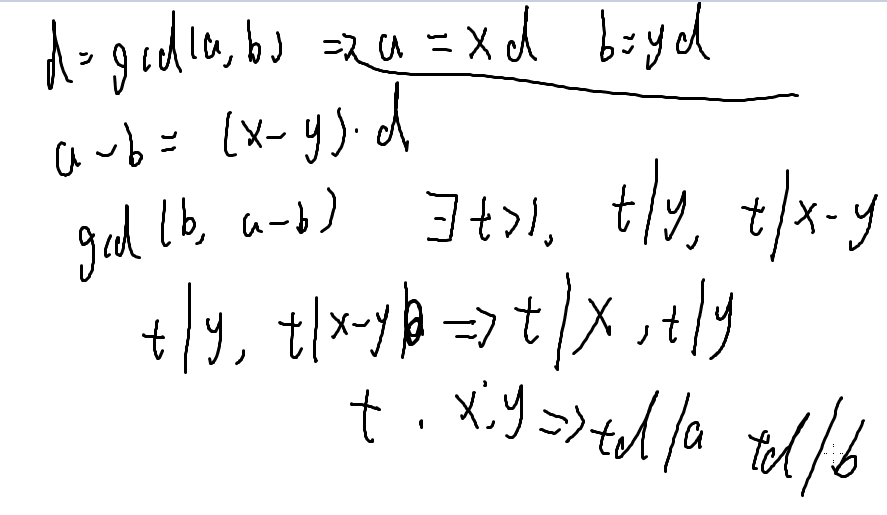
五、裴蜀定理

还有,解释了一下充要条件qqq

证明过程:
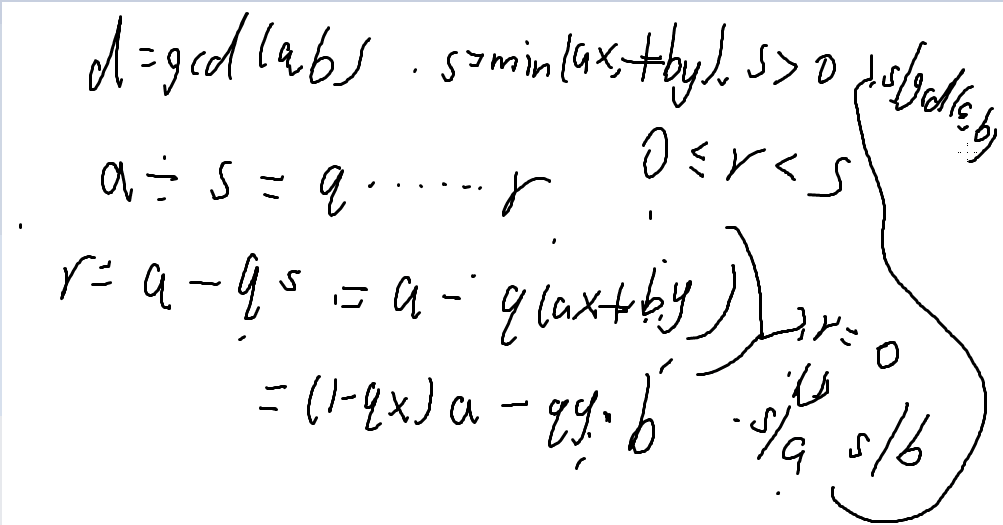
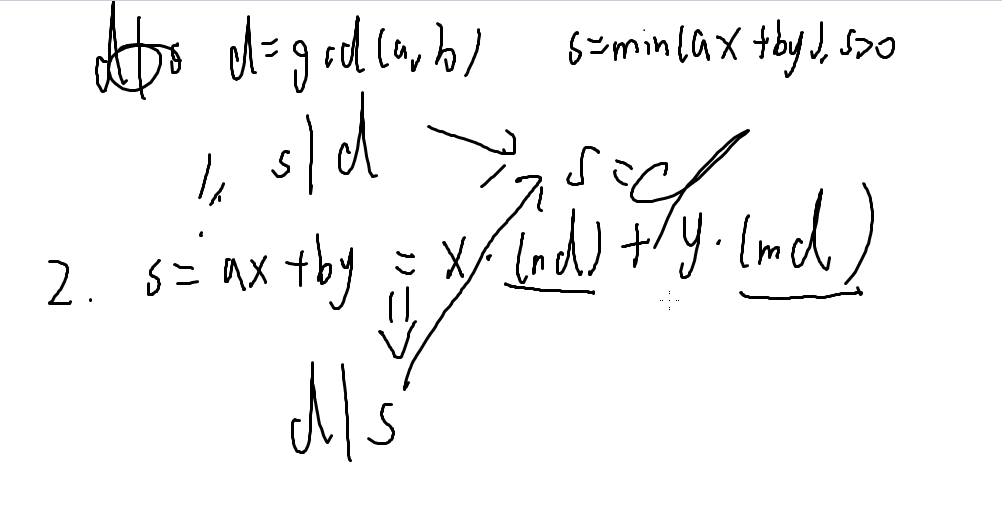
这里可以用裴蜀定理证明这个定理: 设p为质数,若p | ab ,则 p | a或者p | b;
六、拓展欧几里得
求 ax + by = gcd(a,b)的一组解(x,y)
推导式:
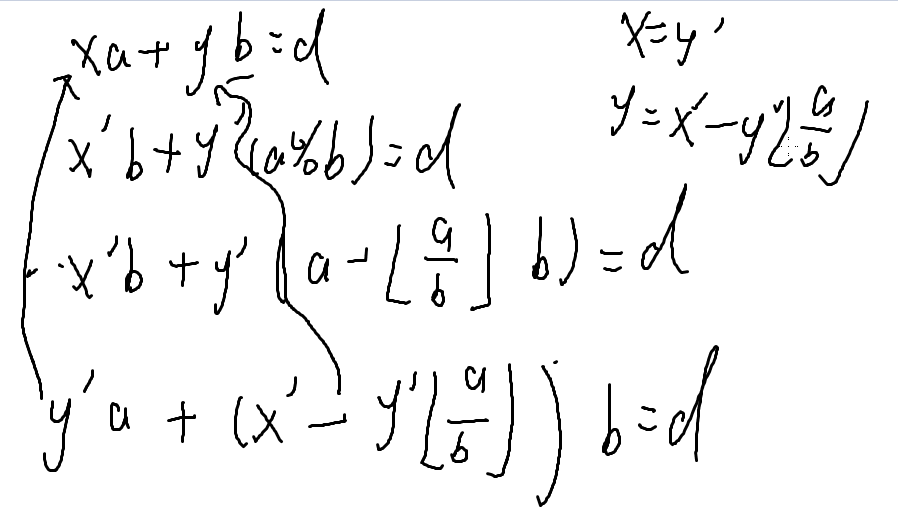
将 a % b 改写为 a - a / b * b
Code:

七、中国剩余定理:


正经做法:
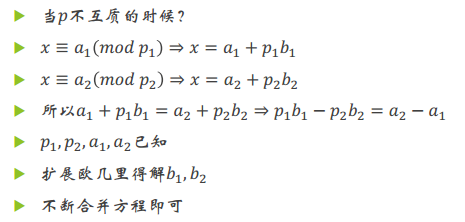
证明过程:
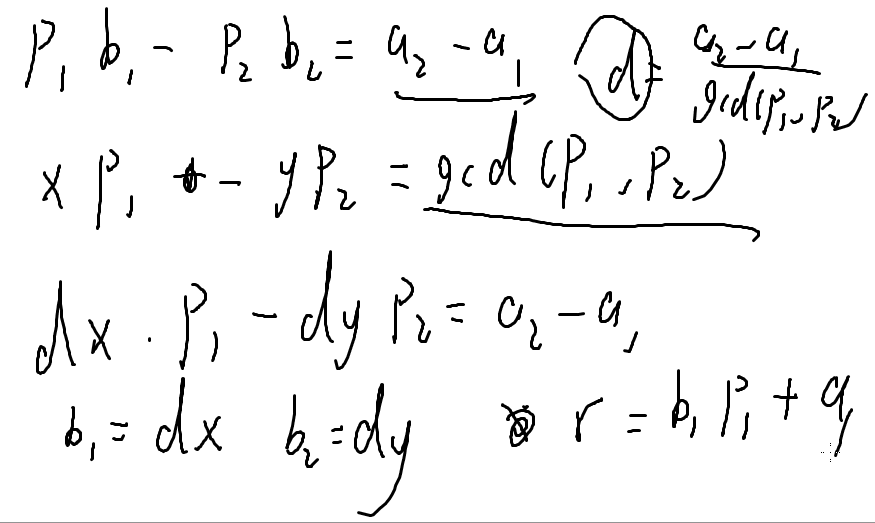
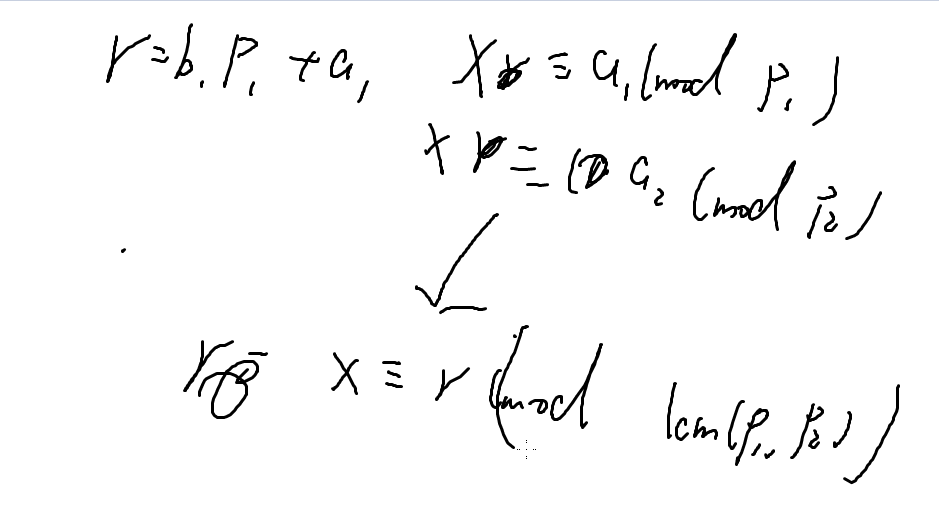
这个题做法即为两两合并
对于k个方程
则进行k - 1次合并
举个栗子:

邪门做法(大数翻倍法):
我们一直对于两个方程式中
不断地将x += p1
直到满足第二个式子
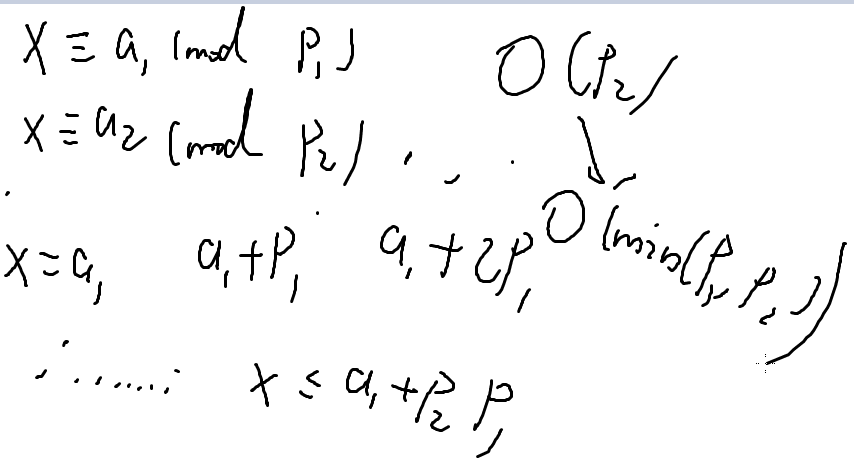
然后对于这个进行排序,选取较大的数
则可得其时间复杂度为: O(p1 + p2 + ... +pn - max(p1,p2,...,pn));
被卡的情况:两个10 ^ 9的p的时候
八、BSGS算法 (Baby Step Giant Step)
qwq(北上广深)(拔山盖世)算法
这个问题主要是求给定a,b,p,求最小的非负整数x,满足 ax ≡ b(mod p)
方法:
r * a ^ sqrt(m) = b;
左右同乘逆元
则变为: r = b * -sqrt(m);
我们可以采用分块:
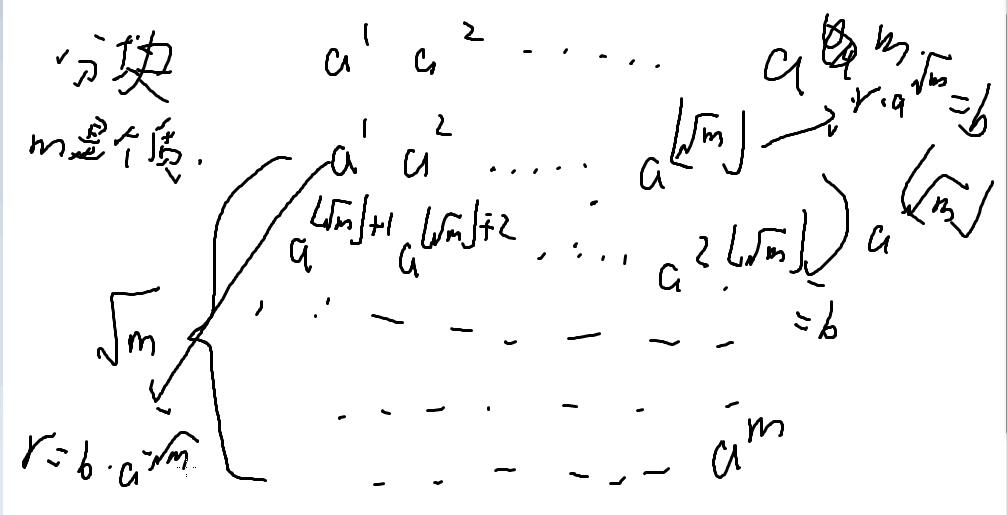
将其分为 sqrt(m) * sqrt(m)的形式
还有一个排序的步骤,便于二分
然后询问在第一行中有没有数可以使得r = b * a ^ -sqrt(m)
Code:
#define ll long long
int size;
bool erfen(int x)
{
int l = 0;
int r = size;
while(l + 1 != r)
{
int m = (l + r) >> 1;
if(z[m] >= x)
r = m;
else
l = m;
}
return z[r] == x;
}
int kuaisumi(int base,int b,int p)
{
int ans;
while(b)
{
if(b & 1)
ans *= base;
base *= base;
b >>= 1;
}
return ans;
}
int bsgs(int a,int b,int p)
{
size = sqrt(p);
int nowv = 1;
for(int i=1;i<=size;i++)
{
nowv = (ll)nowv * a % p;
z[i] = nowv;
if(z[i] == b)
return i;
}
sort(z + 1,z + size + 1);
for(int i=2;(i-1)*size+1<=p;i++)
{
int y =(ll)b * kuaisumi(kuaisumi(a,size * (i - 1),p),p - 2,p);
if(erfen(y))
{
for(int j=(i-1)*size+1;j<=i*size;j++)
if(kuaisumi(a,j,p) == b)
return j;
}
}
return -1;
}
九、线性求逆元
#include<iostream>
#include<cstdio>
#include<algorithm>
#define ll long long
using namespace std;
ll n,p,m,k,r,x;
ll inv[20000528];
int main()
{
scanf("%lld%lld",&n,&p);
inv[1]=1;
if(n<=1)
printf("1\n");
for(int i=2;i<=n;i++)
{
inv[i]=p-(p/i)*inv[p%i]%p;
printf("%lld\n",inv[i]);
}
return 0;
}
九、积性函数
定义:
若gcd(x,y) = 1,有f(xy) = f(x) * f(y)
常见的积性函数:

欧拉函数为积性函数的证明(因子数目与因子之和的大同小异)
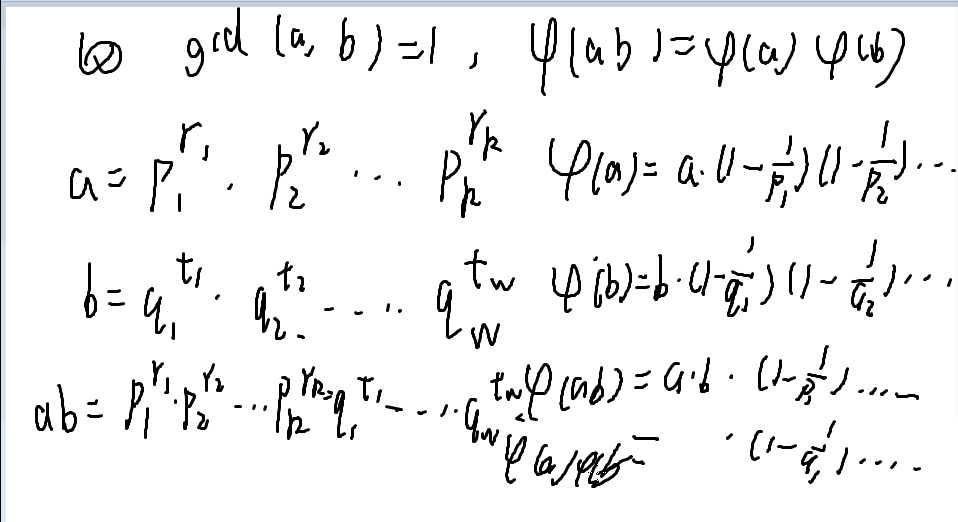
莫比乌斯函数:
mu[i]
对于 i 将其分解(唯一分解定理) 为 p1 ^ r1 ...... pn ^ rn
设 r = max(r1,r2,...,rn);
设 k = r1 + r2 +...+ rn;
则:
mu[i] = 1 i == 1 的时候 mu[i] = 0 r > 1 的时候 mu[i] = (-1) ^ k r == 1 的时候
Code:
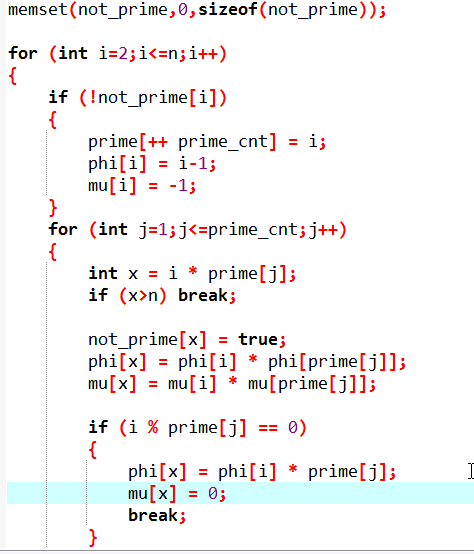
这其中;
phi[] 欧拉函数
mu[] 莫比乌斯函数
线性筛求积性函数
莫比乌斯是积性函数的证明:(这个要用到组合数,长者说明天再讲的)
留个坑,有时间再补吧
十、莫比乌斯反演
F(n)和f(n)是定义在非负整数集合上的两个函数:
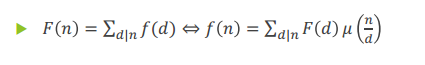
证明:
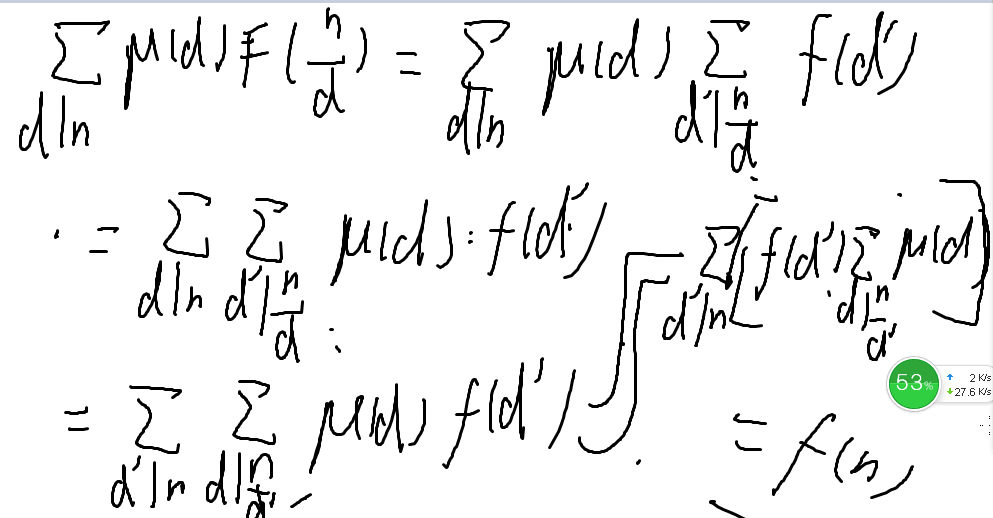
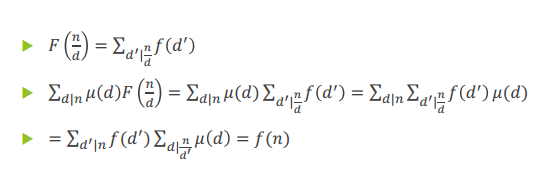
十一、数论函数的卷积
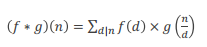
qqq
还有一些老师发的Code:
Miller_Rabin
int gg[8] = {2,3,5,7,13,29,37,89}; bool miller_rabin(int a,int n) { int d=n-1,r=0; while (d%2==0) d/=2,r++; int x = kuaisumi(a,d,n); if (x==1) return true; for (int i=0;i<r;i++) { if (x==n-1) return true; x=(long long)x*x%n; } return false; } bool is_prime(int n) { if (n<=1) return false; for (int a=0;a<8;a++) if (n==gg[a]) return true; for (int a=0;a<8;a++) if (!miller_rabin(gg[a],n)) return false; return true; }
线性筛积性函数中的欧拉函数和莫比乌斯函数
memset(not_prime,0,sizeof(not_prime)); for (int i=2;i<=n;i++) { if (!not_prime[i]) { prime[++ prime_cnt] = i; phi[i] = i-1; mu[i] = -1; } for (int j=1;j<=prime_cnt;j++) { int x = i * prime[j]; if (x>n) break; not_prime[x] = true; phi[x] = phi[i] * phi[prime[j]]; mu[x] = mu[i] * mu[prime[j]]; if (i % prime[j] == 0) { phi[x] = phi[i] * prime[j]; mu[x] = 0; break; } } }


