数论学习(2019.4.4 - 2019.4.7) --4.4

 

 数学基础

一、高精度

介绍就不写了，直接贴代码了

读入读出在最后再加上吧qwq

char str[1000];
int a[1000],b[1000],c[1000];

 

高精 + / -(这两个差不多，一块吧)

for(int i=len-1;i>=0;i--)
    b[len-i] = str[i]-'0';
    int m = len;
    n = max(n,m);
    for(int i=1;i<=n;i++)
    c[i]=a[i]+b[i];
    for(int i=1;i<=n;i++)
    {
        c[i + 1] += c[i]/10;
        c[i] %= 10;
    }
    for(int i=1;i<=n;i++)
    if(c[i]<0)
    {
        c[i] += 10;
        c[i + 1] -= 1;
    }
    while(c[n] == 0)
    n -= 1;

 

高精 *

for(int i=1;i<=n;i++)
    for(int j=1;j<=m;j++)
    c[i + j - 1] += a[i] * b[j];
    for(int i=1;i<=n+m-1;i++)
    {
        c[i + 1] += c[i] / 10;
        c[i] %= 10;
    }
    n = n + m - 1;
    while(c[n + 1] > 0)
    n += 1;

 

高精 /  (B为低精的一个数)

        int B;
    cin>>B;
    for(int i=n;i>0;i--)
    {
        c[i] = a[i]/B;
        a[i - 1] += (a[i] % B) * 10;
    }
    while(c[n] == 0 && n > 0)
    n--;

 

输入输出

        scanf("%s", str);  //输入 
    int len = strlen(str);
    for(int i=len-1;i>=0;i--)
    a[len - i] = str[i] - '0';
        for(int i=n;i>0;i--)  //输出 
    printf("%d",c[i]);

 

二、快速幂：(代码未检查qwq)

1.分治

2.快速幂

 

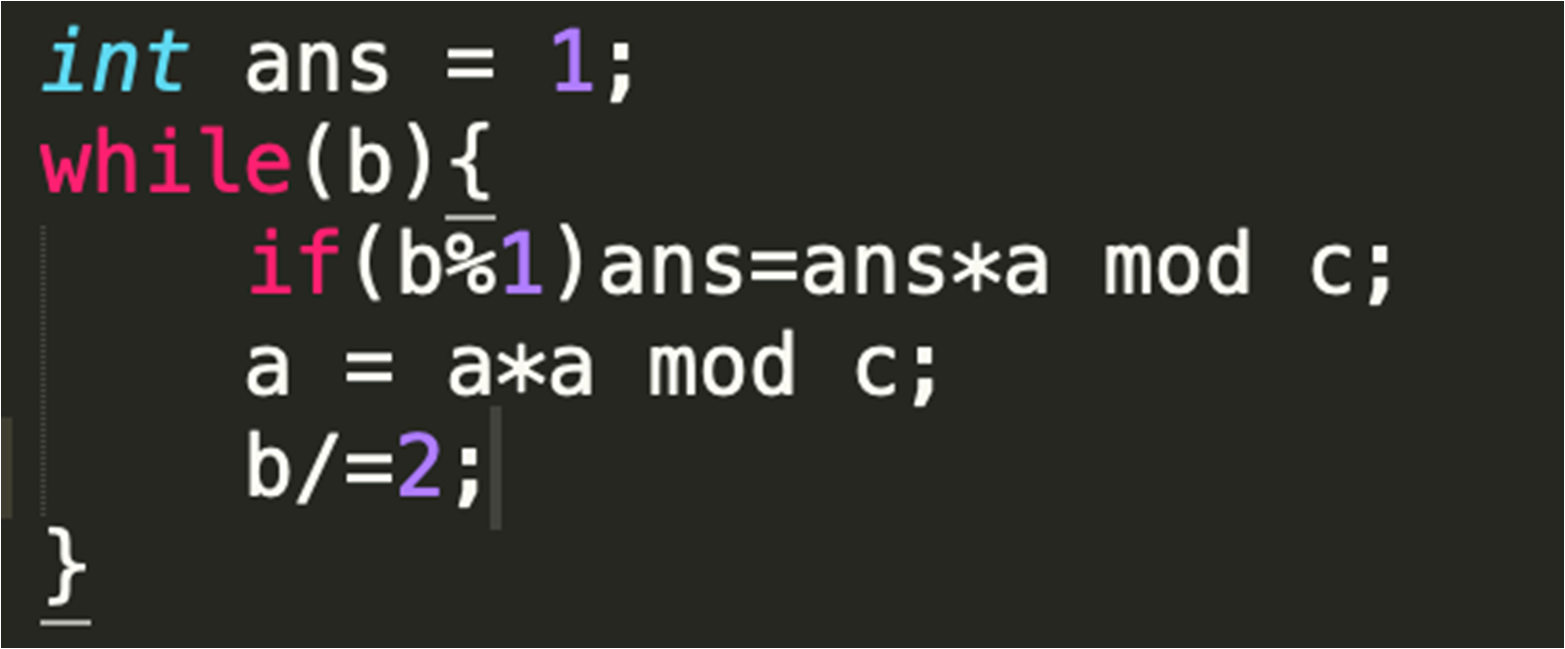
三、费马小定理

应用：

三、(代码未检查qwq)

GCD

LCM

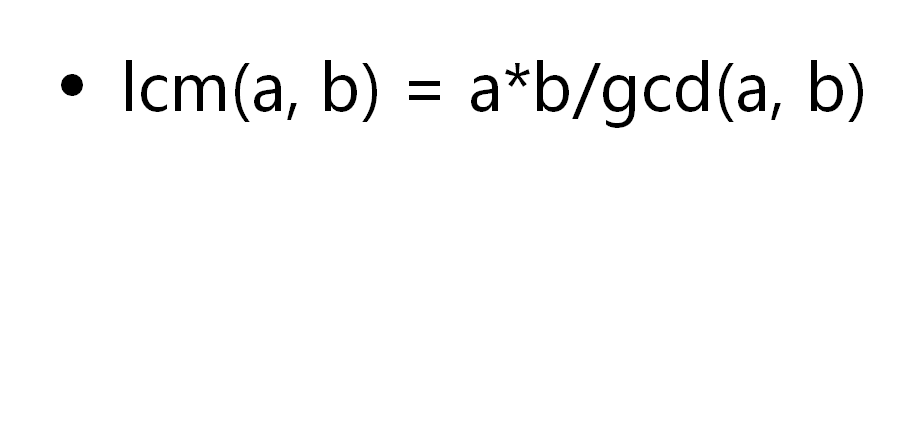
四、质数判别(代码未检查)

1.直接判

............

2.sqrt判别

3.埃氏筛法(O(n loglogn))

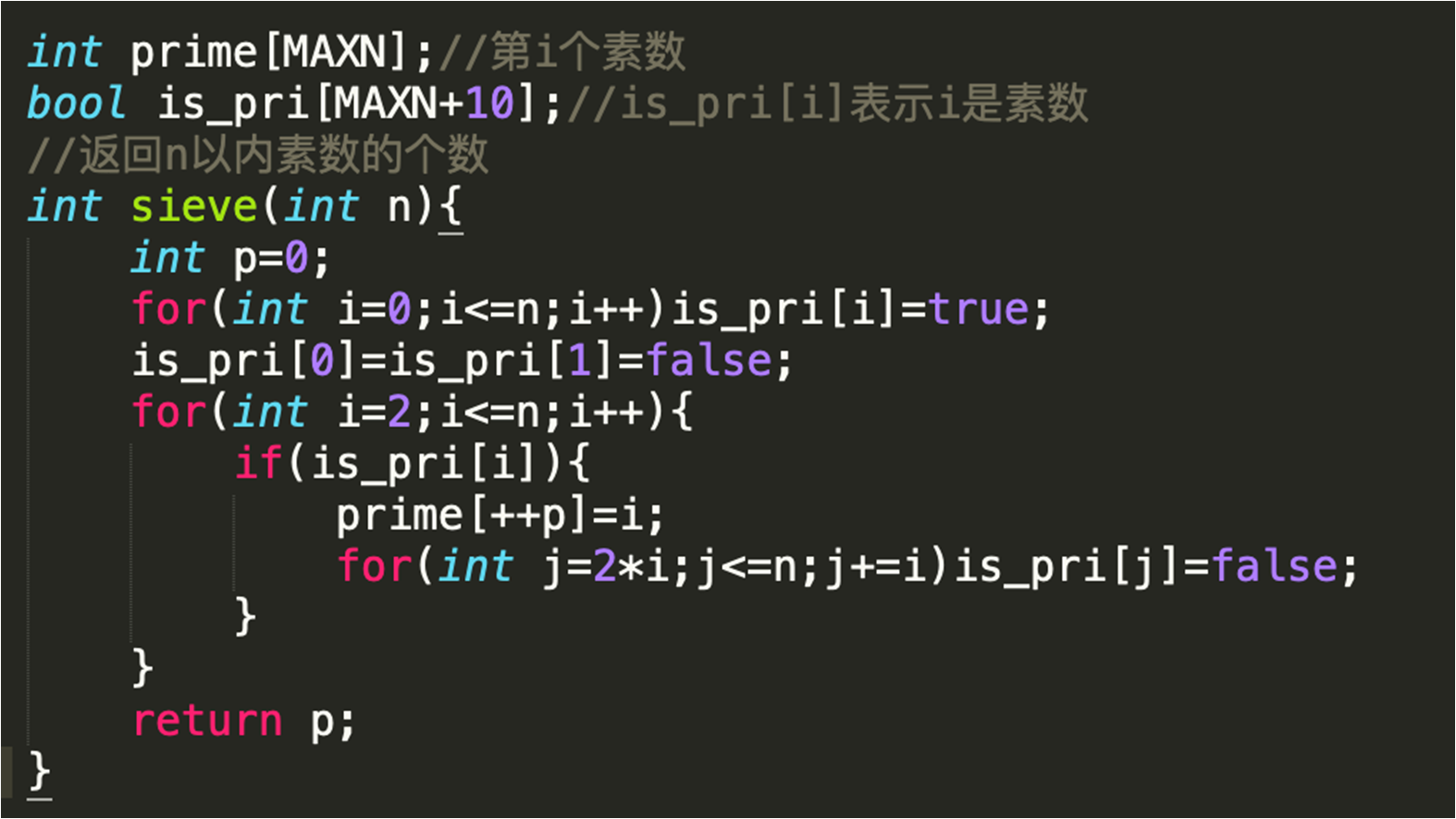
4.线性筛法(接近O(n))

五、Euler

欧拉函数

是小于或等于n的正整数中与n互质的数的数目

欧拉定理

若n,a为正整数，且n,a互素，则

 

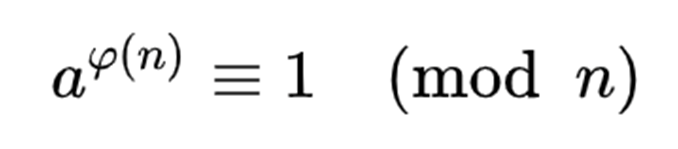
 矩阵

其中满足

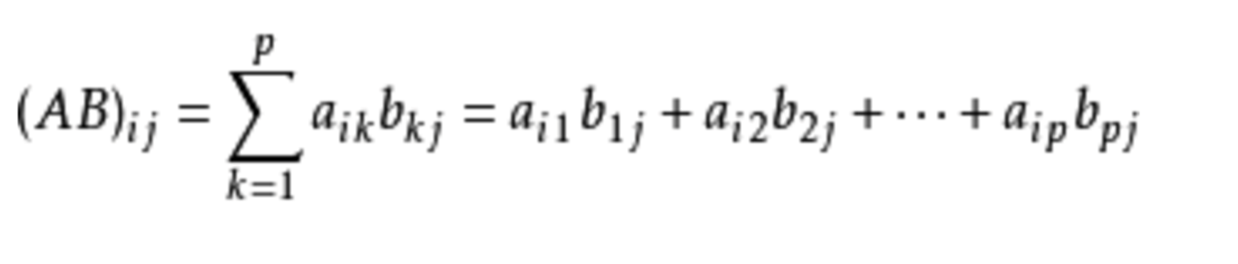
举一个例子：

其中请注意：

矩阵乘法满足结合律、分配率

但是不满足交换律

例：求 f[n] 即斐波那契数列的第n项

其中便是针对于这个进行运算q

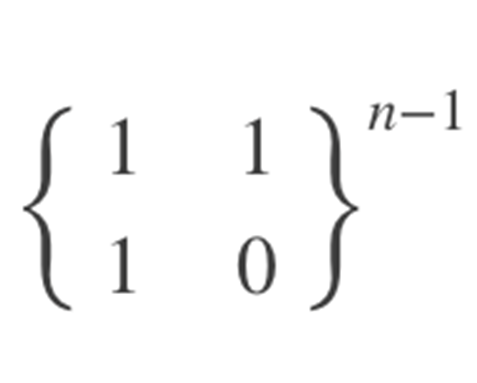
拓展：

若f(n) = 4f(n - 1) - 3f(n - 2) + 2f(n - 4) + b

若f(n) = 4f(n - 1) - 3f(n - 2) + 2f(n - 4) + b

则将变换矩阵改为

 

 

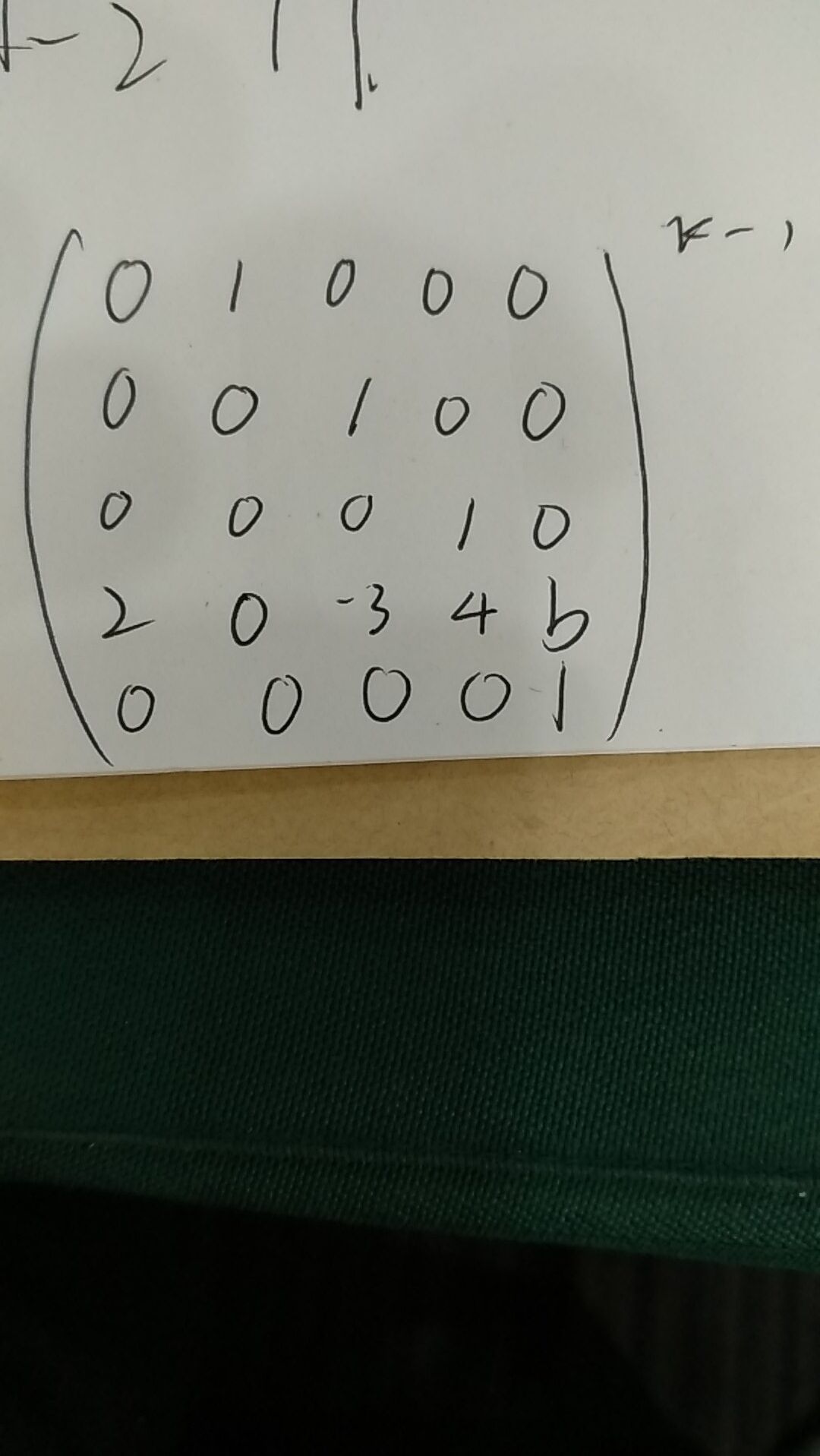
 邻接矩阵的一些应用：

建立邻接矩阵，并对于邻接矩阵进行k次方的运算，得出的结果f[A][B]即为结果

延伸一下：

将刚才的求和改为求最小值min

即为min n i =1 min (a[A][i] * a[i][B]) i 其中的路径

 

一些特殊的矩阵：

上三角矩阵：

 

分块矩阵：

 

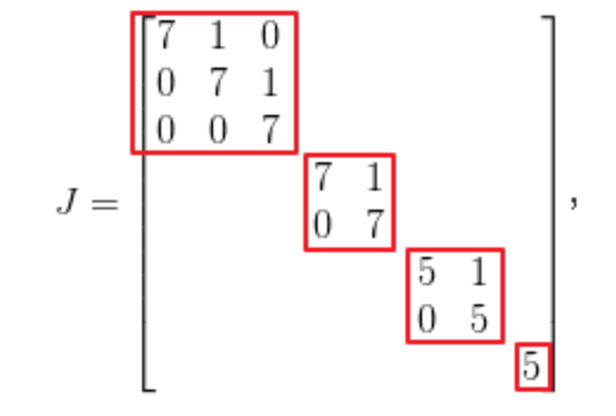
高斯消元：

针对于求解 n 元 1 次线性方程组

形如：

 

举个例子：

 

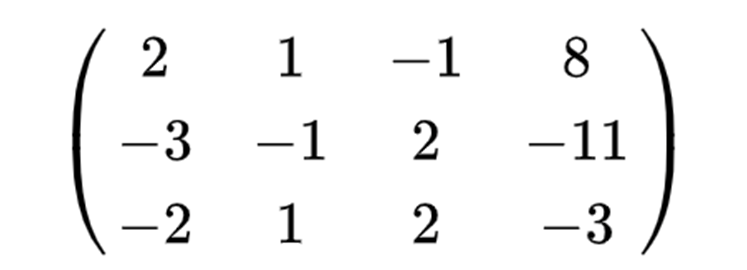
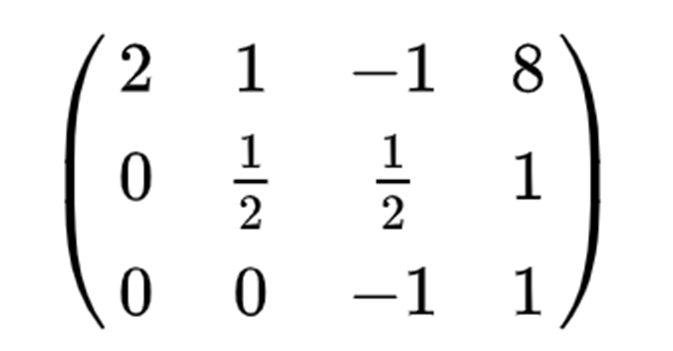
无解的情况：

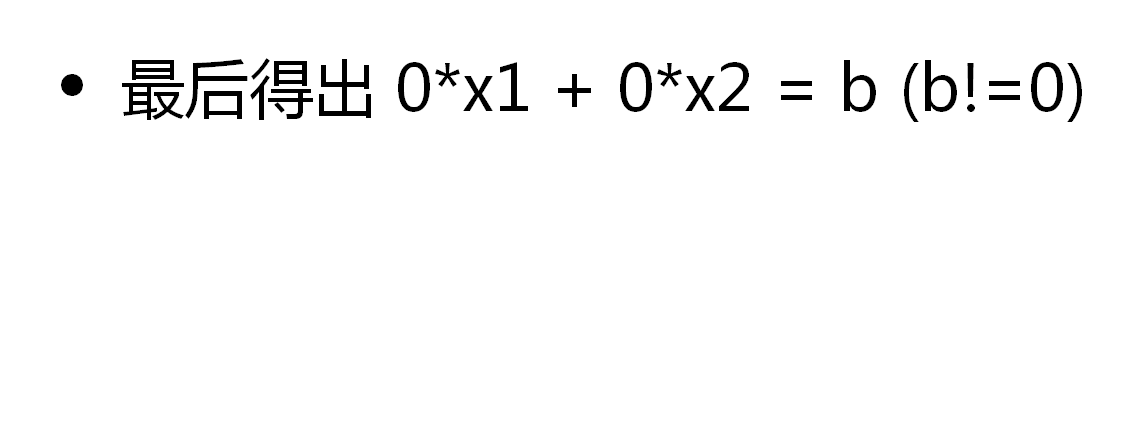
无数解的情况：

 

 

行列式已经学过就不再多提了；

单提一点：

 

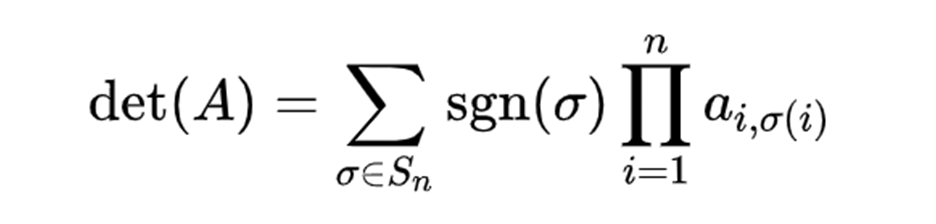
矩阵逆元：

对于A进行变换的同时对于I单位矩阵进行变换

在A到达单位矩阵后I进行相等的变换会得到它的逆元

 

矩阵树定理：

还有一个 k ^ 2 log n求常系数线性递推方程(老师yy出来的)

太晚了...明天再补吧..