树状数组详细解析
本文中或许会引进部分图片来自网络，但大多数内容均为原创qwq。
树状数组或者二叉索引树也称作Binary Indexed Tree，又叫做Fenwick树。
它的查询和修改的时间复杂度都是log(n)，空间复杂度则为O(n).
(这也是我们为什么使用树状数组的原因)
树状数组可以将线性结构转化成树状结构，从而进行跳跃式扫描，通常使用在高效的计算数列的前缀和，区间和，同时，我们在运用线段树的时应先考虑是不是可以使用树状数组来解决问题。
也就是说，在解题思路中，树状数组的优先度是大于线段树的(当然对于神仙们是除外的)
这同样适用于我们针对于排名rank的排序，不过这个时候就需要建立结构体式的树状数组了(我是这么叫的qwq)
下面开始从0入门了：
1.单点查询
我们先从数组讲起(这个就不需要普及了吧)；
A数组是我们传入数据的数组
C数组使我们建立起来的树状数组
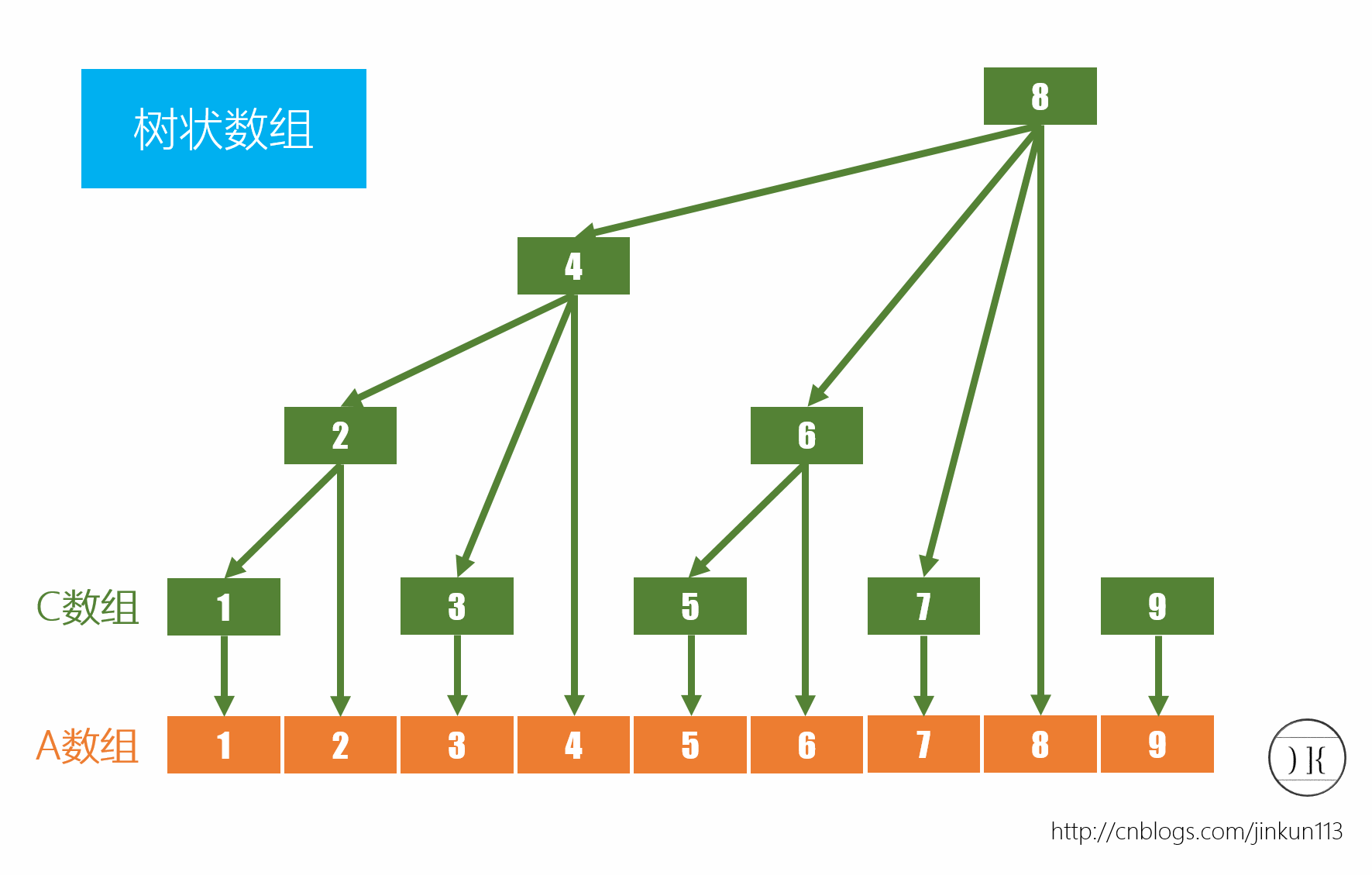
我们通过这里可以显而易见地发现这样一个规律：
C1 = A1 C2 = A1+A2 C3 = A3 C4 = A1+A2+A3+A4 C5 = A5 C6 = A5+A6 C7 = A7 C8 = A1+A2+A3+A4+A5+A6+A7+A8
请大家好好理解上述代码，这是树状数组的基础
接下来我们引入lowbit这个概念：(这个地方有一点需要注意：lowbit(0)会陷入死循环 )
inline int lowbit(int x) { return x & (-x); }
这返回的是这个数字最高位的1;
在这之前，又要引入一个补码的概念：
补码的表示方法是:
正数的补码就是其本身
负数的补码是在其原码的基础上, 符号位不变, 其余各位取反, 最后+1. (即在反码的基础上+1)
[+1] = [00000001]原 = [00000001]反 = [00000001]补
[-1] = [10000001]原 = [11111110]反 = [11111111]补
请注意，这里的第一位是指的是符号位，而不是数字位(这是1，因此数字位只有1)
对于负数, 补码表示方式也是人脑无法直观看出其数值的. 通常也需要转换成原码在计算其数值.
因此，&是求与的一个符号，意思是 a 和 b 同时为 1 的时候返回这个最高位(不包括符号位)
在刚刚的找规律过程中，我们通过规律总结出了以下性质(lowbit是为了帮助程序代码的实现)
我们可以得到树状数组的一些性质：对于c[i]，他的儿子节点取决于i的所有因子中最多有2^j次幂，则向前取2^j个数作为儿子，即[i-2^j+1,i]。(这个时候就需要lowbit来帮助实现)
举一个栗子：
6的最大2次方因子为2，即2^1，则向前取2个数，则c[6]=a[5]+a[6]；
8的最大2次方因子为8，即2^3，则向前取8个数，则c[8]=a[1]+a[2]+...+a[8]。
2.单点修改
当我们要对最底层的值进行更新时，那么它相应的父亲节点存储的和也需要进行更新，
我们建立的树状数组结构是一个完整的结构，因此修改一个点也会需要所有相应的其父亲节点的点来修改，这样我们就实现了树状数组的修改。
代码如下：
void modify(int x,int k) //将 x 增加 k { if(x < 1) return ; while(x <= n) { c[i] += k; x += lowbit(x); //去寻找它的父亲 } }
3.单点查询
单点查询由于我们向前统计，因此需要向前查找，这个就不需要讲了吧(没弄明白请看上面)
int query(int pos)
{
int sum=0;
for(int i=pos;i;i-=lowbit(i))
sum += c[pos];
/*两种写法
while(pos > 0)
{
sum += c[pos];
pos -= lowbit(pos);
}
*/
return sum;
}
至此为止，我们已经讲完了树状数组的基础内容。
贴一下基础部分的代码：
void change(int p, int x) { //给位置p增加x while(p <= n) { sum[p] += x; p += p & -p; } } int ask(int p) { //求位置p的前缀和 int res = 0; while(p) { res += sum[p]; p -= p & -p; } return res; } int query(int l, int r) { //区间求和 return ask(r) - ask(l - 1); }
请确保在以上内容均熟练掌握的情况下再学习以下知识点。
在进入接下来的学习中，建议先做一下这几个题
以上这些只是我们学习树状数组的基础，真正的高端树状数组是可以在很大的范围内进行局部优化和大幅度降低复杂度的
举一个小栗子：
当我们在面对很大的数据范围的时候，就可以先离散化，再针对其进行树状数组的一个对应关系
放心，这只是我们面对于数据组的优化，而既然是树状数组，便肯定不会受限于这一些东西；
接下来开始正题：
4.区间修改与单点查询
对于这种问题的思路就是对于题目所给出的区间进行差分的操作。
如果不知道差分的同学请补习之后再来
查询：
设原数组为a[i]；
设数组c[i] = a[i]−a[i−1](a[0]=0)
c[i] = a[i]−a[i−1](a[0]=0)；
则 a[i]= ∑i j=1 c[j]
可以通过求c[i]的前缀和查询。
修改：
当给区间[l,r]加上x的时候；
a[l]与前一个元素a[l−1] 的差增加了x；a[r+1]与 a[r]的差减少了x。
根据c[i]数组的定义，只需给a[l]加上x, 给a[r+1]减去x即可。
Codes:
void add(int p, int x) { while(p <= n) { c[p] += x; p += lowbit (p); } } void range_add(int l, int r, int x) { add(l, x); add(r + 1, -x); } int ask(int p) { int res = 0; while(p) { res += sum[p],; p += lowbit (p); } return res; }
5.区间修改与区间查询
这个地方是我们在线段树中的重点与难点(lazytag)，但是如今我们有了树状数组，于是便可以有另一种方法来解决它了；
怎么求呢？我们基于问题2的“差分”思路，考虑一下如何在问题2构建的树状数组中求前缀和：
位置p的前缀和如下：
∑p i=1 a[i] = ∑ p i=1 ∑ i j=1 c[j]
哇，写这个式子真的难受
当我们发现在这里
c[1]被使用了p次；
c[2]被使用了p-1次；
~~~~
我们就可以针对于这个式子进行改进：
∑ p i=1 ∑ i j=1 c[j] = ∑p i=1 c[i] ∗ (p − i + 1) = (p + 1) ∗ ∑ p i=1 c[i] − ∑ p i=1 c[i] ∗ i
这样我们便可以建立两个数组进行维护前缀和：
sum1[i]=d[i]；
sum2[i]=d[i]∗i
查询：
p位置的前缀和便是在sum1中(p + 1)的前缀和减去sum2中p位置的前缀和
那么区间[l,r]的前缀和就是r的前缀和减去l的前缀和
修改：
因为我们对于sum1的修改同于问题二中的修改
对于sum2的修改是对于sum2[l] 加上 l * x，给 sum2[r + 1] 减去 (r + 1) * x。
用这个做区间修改区间求和的题，无论是时间上还是空间上都比带lazytag的线段树要优。
(这也是为什么树状数组的初步价值)
Codes:
#define ll long long void add(ll p, ll x) { for(int i = p; i <= n; i += lowbit(i)) { sum1[i] += x; sum2[i] += x * p; } } void range_add(ll l, ll r, ll x) { add(l, x); add(r + 1, -x); } ll ask(ll p) { ll res = 0; for(int i = p; i; i -= lowbit(i)) res += (p + 1) * sum1[i] - sum2[i]; //重点 return res; } ll range_ask(ll l, ll r) { return ask(r) - ask(l - 1); }
6.二维树状数组
我们已经学会了对于序列的常用操作，那么对于矩阵呢，还记得这个梦么(蒟蒻我看不懂什么神仙题)
能不能把类似的操作应用到矩阵上呢？这时候我们就要写二维树状数组了！
在一维树状数组中，c[x]记录的是右端点为x、长度为lowbit(x)的区间的区间和。
那么在二维树状数组中，可以类似地定义c[x][y]记录的是右下角为(x, y)，高为lowbit(x), 宽为 lowbit(y)的区间的区间和。
好的，很好qwq，这个地方的操作实际上是类似于一维的；
而且理解起来也不是很难，看着代码也许会好一些吧q
单点修改与区间查询：
void add(int x, int y, int z) //将点(x, y)加上z { int lasty = y; while(x <= n) { y = lasty; while(y <= n) //因为是修改，所以一直到(n,n)都要修改 { tree[x][y] += z; y += lowbit(y); } x += lowbit (x); } } void ask(int x, int y) //求左上角为(1,1)右下角为(x,y) 的矩阵和 { int res = 0 int lasty = y; while(x) { y = lasty; while(y) { res += tree[x][y]; y -= lowbit(y); } x -= lowbit(x); } }
区间修改和单点查询
这个需要用的二维数组的前缀和
二维的前缀和就差不多长这样
其实二维的前缀和在实现的时候还是有不少的困难的，但是这并不是我们在今天所主要涉及的内容，
如果对于二维数组的前缀和不是很理解请戳这里或者上网自行百度
Codes：
void add(int x, int y, int z) { int lasty = y; while(x <= n) { y = lasty; while(y <= n) { tree[x][y] += z; y += lowbit(y); } x += lowbit(x); } } void range_add(int xa, int ya, int xb, int yb, int z){ add(xa, ya, z); add(xa, yb + 1, -z); add(xb + 1, ya, -z); add(xb + 1, yb + 1, z); } void ask(int x, int y) { int res = 0l; int lasty = y; while(x) { y = lasty; while(y) { res += tree[x][y]; y -= y & -y; } x -= lowbit(x); } }
这个远远不是想象中的那样难，只是相当于对于一个二维数组进行了压缩。
对于二维数组里的内容起到了一个区域求值的方法，这也是树状数组的核心所在
区间修改和区间查询
(截图markdown真好用！)
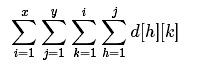
这个式子一般就是我们在面对二维数组求区间和的问题时候的究极无敌暴力策略吧...
显然是可以卡回祖宗的
这个时候再找一下规律，我们又会发现：
d[1][1]出现了x∗y次
d[1][2]出现了x∗(y−1)次……
d[h][k]出现了 (x−h+1)∗(y−k+1)次。
这说明了(找规律大法好)我们可以对于这个进行树状数组优化：
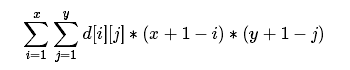
我们对于这个式子进行多项式运算，就会有以下的这些过程
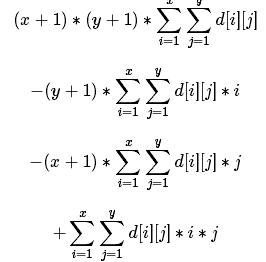
这样我们就只需要开四个树状数组，分别维护四个变量就足够了
sum1[]维护 c[i][j]
sum2[]维护 c[i][j] * i
sum3[]维护 c[i][j] * j
sum4[]维护 c[i][j] * i * j
就完成了操作了！
贴一个简单点的代码：
Codes1：
#define ll long long #define RI register int int n,m,last,opt,x,y,z,mian，opt; int sum1[500002],sum2[500002]; int lowbit(int x) { return x & (-x); } void in(int &x) int f = 1; x = 0; char ch = getchar(); while(ch > '9' || ch < '0') { if(s == '-') f = -1; ch = getchar(); } while(ch <= '9' && ch >= '0') { x = x * 10 + s - '0'; ch = getchar(); } x *= f; } void add(int pos,int x) { for(RI i=pos;i<=n;i+=lowbit(i)) sum1[i]+=x,sum2[i]+=pos*x; } ll query(int pos) { long long res=0; for(RI i=pos;i;i-=lowbit(i)) res += (pos + 1) * sum1[i] - sum2[i]; return res; } int main() { in(n); in(m); for(RI i=1;i<=n;i++) { in(x); add(i,x-last); last=x; } for(RI i=1;i<=m;i++) { in(opt); switch(opt) { case 1:in(x),in(y),in(z),add(x,z),add(y+1,-z);break; case 2:in(z),mian+=z;break; case 3:in(z),mian-=z;break; case 4: { in(x),in(y); if (x == 1) printf("%lld\n",query(y) - query(x - 1) + mian); else printf("%lld\n",query(y) - query(x - 1)) break; } case 5:printf("%lld\n",query(1) + mian); } } return 0; }
Codes2:(代码搬砖自胡小兔)
#include <cstdio> #include <cmath> #include <cstring> #include <algorithm> #include <iostream> using namespace std; typedef long long ll; ll read(){ char c; bool op = 0; while((c = getchar()) < '0' || c > '9') if(c == '-') op = 1; ll res = c - '0'; while((c = getchar()) >= '0' && c <= '9') res = res * 10 + c - '0'; return op ? -res : res; } const int N = 205; ll n, m, Q; ll t1[N][N], t2[N][N], t3[N][N], t4[N][N]; void add(ll x, ll y, ll z){ for(int X = x; X <= n; X += X & -X) for(int Y = y; Y <= m; Y += Y & -Y){ t1[X][Y] += z; t2[X][Y] += z * x; t3[X][Y] += z * y; t4[X][Y] += z * x * y; } } void range_add(ll xa, ll ya, ll xb, ll yb, ll z){ //(xa, ya) 到 (xb, yb) 的矩形 add(xa, ya, z); add(xa, yb + 1, -z); add(xb + 1, ya, -z); add(xb + 1, yb + 1, z); } ll ask(ll x, ll y){ ll res = 0; for(int i = x; i; i -= i & -i) for(int j = y; j; j -= j & -j) res += (x + 1) * (y + 1) * t1[i][j] - (y + 1) * t2[i][j] - (x + 1) * t3[i][j] + t4[i][j]; return res; } ll range_ask(ll xa, ll ya, ll xb, ll yb){ return ask(xb, yb) - ask(xb, ya - 1) - ask(xa - 1, yb) + ask(xa - 1, ya - 1); } int main(){ n = read(), m = read(), Q = read(); for(int i = 1; i <= n; i++){ for(int j = 1; j <= m; j++){ ll z = read(); range_add(i, j, i, j, z); } } while(Q--){ ll ya = read(), xa = read(), yb = read(), xb = read(), z = read(), a = read(); if(range_ask(xa, ya, xb, yb) < z * (xb - xa + 1) * (yb - ya + 1)) range_add(xa, ya, xb, yb, a); } for(int i = 1; i <= n; i++){ for(int j = 1; j <= m; j++) printf("%lld ", range_ask(i, j, i, j)); putchar('\n'); } return 0; }
好了。
完结撒花，其实还有一些知识点，想起来再更新吧。
码量惊人，客官点个推荐吧qwq
