由一个算法题引发的哈夫曼树讲解

1.请听题

 

 由上面计算可得，c的长度总和最小，也就是最优二叉树，也是哈夫曼树。

定义：叶子节点带权路径长度和最小的树的结构就是最优二叉树

2.怎么构造哈夫曼树

 1）选最小的两个结点（可通过优先队列选），小的数在左边，大的在右边成

 2）生成父节点，该结点权重为两个子节点之和

 3）除去已被选的结点，新增新生成的结点，再选出最小的两个结点.....以此类推，最终生成哈夫曼树

举个栗子：

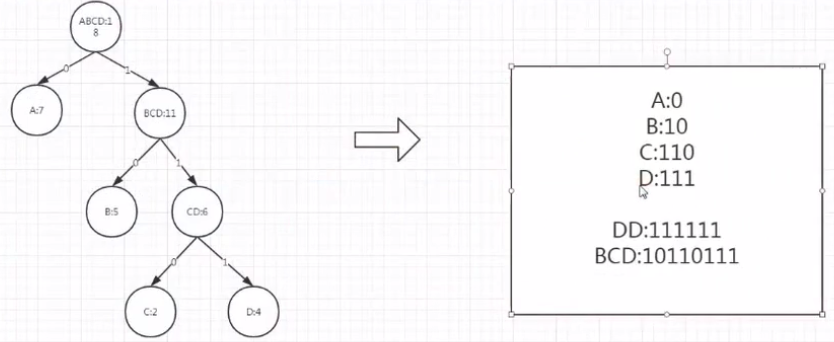
a:7   b:5   c:2   d:4   四个结点生成哈夫曼树

1）选出最小的c和d，并生成cd结点，且得到权重为2+4=6

2）再从a、b、cd中找到最小的两个，b和cd，并生成bcd，且得到权重为5+6=11

3）再从a、bcd中找到最小两个，并生成abcd，且得到权重7+11=18

如下图

再把左边分支都设置为0，右边分支都设置为1，即可得到abcd的加密后密文，如下图，这就是哈夫曼的编码功能。

由于转成二进制，为byte，所以大大减少内存，故也可以用哈夫曼进行压缩。

由于ABCD的二进制编码不可能为彼此结点的前缀，故属于前缀树，例如：111111可推出DD，故哈夫曼编码是可逆的。

 

 3.哈夫曼树的应用

由以上可得出，当然，实际也是如次，哈夫曼树常用于加密、压缩，常用语通信行业。

4.怎么确定权重

某本书某个字出现的次数就作为权重