关于信息熵的知识整理

1、我没有学过信息论，但学过信息安全相关的知识。第一次接触到信息熵，是计网的物理层的编码解码过程，老师只是简单地提了熵的公式，大概解释了这个公式是怎么来的，后面再听到这个概念，已经是密码学的课程了。因为近期用到这方面的知识，整理一下。之后有用到新的知识会再次添加的。

参考 信息熵及其相关概念

 

2、信息熵的定义公式

 

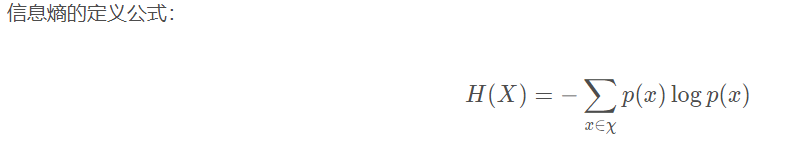
这个公式是结论，理解这个公式需要理解信息熵是什么、信息熵的三条性质。

 

3、信息熵的性质

信息论之父克劳德·香农给出的信息熵的三个性质[1]：

单调性，发生概率越高的事件，其携带的信息量越低（事件发生的概率越低，其发生时所能给出的信息量越大）；
非负性，信息熵可以看作为一种广度量，非负性是一种合理的必然；
累加性，即多随机事件同时发生存在的总不确定性的量度是可以表示为各事件不确定性的量度的和，这也是广度量的一种体现。

对于累加性，有两个理解。

如果认为事件由多个环节组成，每个环节又有多个可能，那么，

第一，一个事件的所有环节的熵等于该事件的各个环节的熵之和

第二，一个环节的所有可能的熵等于每个可能的熵之和

这里的事件对应密钥，环节对应比特，而可能对应一个比特可能存在的0、1两种可能。这样理解对吗？

实际上不能简单地通过累加性这么理解，但因为密钥的每个bit之间是相互独立的，所以，结论是对的？

 

香农从数学上严格证明了满足上述三个条件的随机变量不确定性度量函数具有唯一形式，

 

 

 

 

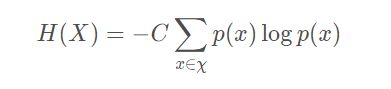
其中的 C为常数，我们将其归一化为 C = 1即得到了信息熵公式。

 4、对三条性质的理解

回过头来再看信息熵的公式，其中对概率取负对数表示了一种可能事件发生时候携带出的信息量。把各种可能表示出的信息量乘以其发生的概率之后求和，就表示了整个系统所有信息量的一种期望值。从这个角度来说信息熵还可以作为一个系统复杂程度的度量，如果系统越复杂，出现不同情况的种类越多，那么他的信息熵是比较大的。如果一个系统越简单，出现情况种类很少（极端情况为 1种情况，那么对应概率为 1，那么对应的信息熵为 0），此时的信息熵较小。

 

5、伯努利分布熵的计算