普通Splay详解
预备知识:
至于BST,随便看一下就可以,
我们知道二叉搜索树是O(logN)的,那我们为什么要用平衡树呢?
之前我们了解到,BST的插入是小的往左子树走,大的往右子树走,如果凉心出题人给出的序列是有序的呢
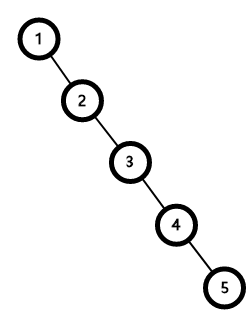
这样我们就只能O(N)的操作,GG
旋转(rotate):
Splay的经典操作就是旋转
在Splay中,我们用旋转来保持平衡,也就是保持是log(N)的量级
旋转就是将节点向上旋转到父亲节点的位置,同时保持平衡
有zig,和zag两种情况(其实都一个样)
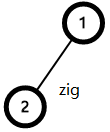
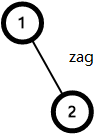
具体要怎么旋转呢
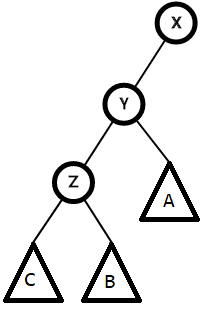
如图,X,Y,Z 是三个节点,A,B,C 是三颗子树,我们要把 Z 转到 Y 的位置
其实就只有3步
根据平衡树的性质
Z 是 Y 的左儿子,所以Z < Y
Y 是 X 的左儿子,所以Y < X
我们要把 Z 旋转上去的话,就把 Z 放到 Y 的位置
整完了长这样
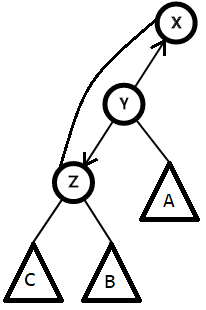
因为我们还没操作 Y,所以Y还有连向其父亲和儿子的边
总结一下
Step1:把要旋转的节点放到父亲的位置
而 Y > Z 且 Y < X,所以这时Y就成了Z的右儿子
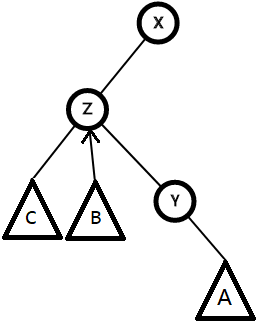
总结一下
Step2:把要旋转节点的父亲设为其儿子
这时会有三个节点(子树)连向 Z,而Y只有一个儿子,显然,Z,子树 B 和子树 C 都是小于 Y 的,子树 B 大于 Z,所以 B 成为 Y 的左儿子
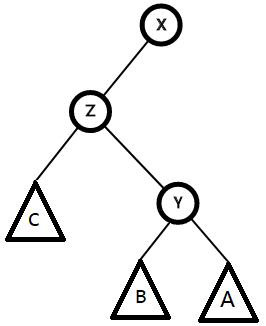
这样就完成了
总结一下
Step3:把 父节点所占旋转节点的儿子 设为父节点的对应儿子
代码:
定义一波:
struct tree {
int fa, cnt, sum, val;
//父亲
//计数(几个值为x的点)
//以当前点为根节点的子树节点个数
//当前点的值
int ch[2];
//左右儿子,0为左儿子,1为右儿子
} t[N];
关于获得这个节点是左儿子还是右儿子:
inline int get(int x) {
return t[t[x].fa].ch[0] == x ? 0 : 1;
}
更新:
inline void pushup(int x) {
t[x].sum = t[t[x].ch[0]].sum + t[t[x].ch[1]].sum + t[x].cnt;
}
旋转:
inline void rotate(int x) {
int fa = t[x].fa, gfa = t[fa].fa;//父亲和爷爷
int k = get(x);//x是其父节点的那个儿子
//step1
t[x].fa = gfa;
t[gfa].ch[get(fa)] = x;
//step2
t[t[x].ch[k ^ 1]].fa = fa;
t[fa].ch[k] = t[x].ch[k ^ 1];
//step3
t[fa].fa = x;
t[x].ch[k ^ 1] = fa;
pushup(fa), pushup(x);
//因为旋转后父节点成了当前点的子节点,所以先更新父亲
}
关于为什么是 k ^ 1,假设我们要旋转的点是左儿子,那他的父亲一定会成为他的右儿子,同理,如果要旋转的点是左儿子,他的父节点一定会成为他的右儿子
伸展(splay)
splay操作就是把一个点旋转到指定的点
最容易想到的,就是一直旋转到指定的节点,然而这样是错的

这时我们就要用到双旋,双旋有两大种四小种情况
1、zig-zig或zag-zag
当节点是父亲的左儿子且父节点是祖父节点的左儿子
或节点是父亲的右儿子且父节点是祖父节点的右儿子
先旋转父亲,再旋转自己
借用一下GeeksofrGeeks的图:
Zig-Zig (Left Left Case):
G P X
/ \ / \ / \
P T4 rightRotate(G) X G rightRotate(P) T1 P
/ \ ============> / \ / \ ============> / \
X T3 T1 T2 T3 T4 T2 G
/ \ / \
T1 T2 T3 T4
Zag-Zag (Right Right Case):
G P X
/ \ / \ / \
T1 P leftRotate(G) G X leftRotate(P) P T4
/ \ ============> / \ / \ ============> / \
T2 X T1 T2 T3 T4 G T3
/ \ / \
T3 T4 T1 T2
2.zig-zag或zag-zig
当节点是父亲的左儿子且父节点是祖父节点的右儿子
或节点是父亲的右儿子且父节点是祖父节点的左儿子
旋转两次自己
再次借用GeeksforGeeks的图:
Zag-Zig (Left Right Case):
G G X
/ \ / \ / \
P T4 leftRotate(P) X T4 rightRotate(G) P G
/ \ ============> / \ ============> / \ / \
T1 X P T3 T1 T2 T3 T4
/ \ / \
T2 T3 T1 T2
Zig-Zag (Right Left Case):
G G X
/ \ / \ / \
T1 P rightRotate(P) T1 X leftRotate(P) G P
/ \ =============> / \ ============> / \ / \
X T4 T2 P T1 T2 T3 T4
/ \ / \
T2 T3 T3 T4
代码:
inline void splay(int x, int pos) {
while (t[x].fa != pos) {//一直旋转成为目标位置的儿子
int fa = t[x].fa, gfa = t[fa].fa;
if (gfa != pos) (t[gfa].ch[0] == fa) ^ (t[fa].ch[0] == x) ? rotate(x) : rotate(fa);//判断是哪个儿子并旋转
rotate(x);//无论哪种情况都要旋转x
}
if (pos == 0) root = x;
}
插入(insert)
对于一个新的值x
如果x等于根的值,从根节点开始比较节点的val值
如果x==val的话,这个点的计数器++,
x小于val的话向左搜,x大于val的话向右搜
如果不存在某个点的val是x,这时我们即使搜到最底端也没有找到,就直接新建这个节点
因为在插入时可能会形成一条链,在最后的时候还要splay一下把新插入的节点转为根
代码:
inline void insert(int x) {
int u = root, fa = 0; //当前位置u,父节点fa
while (u && t[u].val != x) { //当u不存在且u的值不等于x。······①
fa = u; //向下找u的儿子,父亲为u
u = t[u].ch[x > t[u].val]; //大于当前位置u向右找,小于向左找
}
if (u) t[u].cnt++; //如果有一个节点的值等于x,计数器++
else {
u = ++tot; //新节点的位置
if (fa) t[fa].ch[x > t[fa].val] = u; //如果父节点非根
t[u].ch[1] = t[u].ch[0] = 0; //没有儿子
t[u].fa = fa, t[u].val = x, t[u].cnt = 1, t[u].sum = 1;
}
splay(u, 0); //旋转保持树的平衡
}
查找(find)
与操作插入操作相似
只需要向左右子树找所查找的数
如果当前点的值等于所查找的数,把当前节点splay到根
inline void find(int x) { //查找x的位置并旋转到根
int u = root;
if (!u) return ; //空树
while (t[u].ch[x > t[u].val] && x != t[u].val) //存在儿子且当前节点的值不等于x。······②
u = t[u].ch[x > t[u].val];//跳转到儿子
splay(u, 0); //旋转到根
}
在初学的时候在这里糊了一下,在这里稍微说明
在insert和find中,一个是当u存在(①),一个是当u的儿子存在(②),当时还试着改了一下代码,结果
其实也很简单
在插入的时候,如果没有一个节点的值等于x,我们在找的时候u会找到树外(u为0,就表示了这个节点不存在),这时我们就新建节点
在查找的时候,不能找出树外,所以要判断u对应的子节点是否存在,不能让u跑到树外面
前驱/后继(nx)
先find一下,把要找的数先转到根
以后继为例,确定后继比x大,所以在右子树里找
有因为后继是右子树里最小的,就在右子树一直向左找,找到叶节点
前驱相反
inline int nx(int x, int f) { //0 next;1 pre
find(x);
int u = root;
if (t[u].val > x && f) return u;//如果当前节点的值大于x并且要查找的是后继
if (t[u].val < x && !f) return u;//如果当前节点的值小于x并且要查找的是前驱
u = t[u].ch[f]; //前驱在左子树里找,后继在右子树里找
while (t[u].ch[f ^ 1]) u = t[u].ch[f ^ 1];//在另一个方向上找
return u;
}
第k小的数(rank)
先判断一下是不是有这么多数
看一下左子树的大小,如果k小于左子树大小的话就在左子树里找第k小
如果k大于(左子树大小+当前节点的个数),在右子树上找第(k-左子树大小-当前节点的个数)小
否则,就是根节点的值
inline int rank(int x) {
int u = root;
if (t[u].sum < x) return 0; //没有这么多节点
while (1) {
int v = t[u].ch[0]; //左子树
if (x > t[v].sum + t[u].cnt) { //如果排名大于左子树的大小+当前节点的数量
x -= t[v].sum + t[u].cnt;
u = t[u].ch[1]; //当前排名的数一定在右儿子上
} else if (t[v].sum >= x) u = v; //在左子树上
else return t[u].val; //根节点
}
}
删除(Del)
删除一个点的话
把前驱转到根,把后继转到前驱的下面
后继比前驱大,在前驱的右子树,当前数比前驱大,在前驱的右子树
而在右子树内比后继小的只有当前数,在后继的左子树,所以直接删去后继的左子树
inline void Del(int x) {
int last = nx(x, 0), nxt = nx(x, 1); //前驱,后继
splay(last, 0), splay(nxt, last);
int del = t[nxt].ch[0]; //后继的左子树
if (t[del].cnt > 1) { //超过一个
t[del].cnt--; //计数--
splay(del, 0);
} else t[nxt].ch[0] = 0; //删除
}
模板:

#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
int n, m, tot, root;
struct tree {
int fa, cnt, sum, val;
int ch[2];
} t[N];
template<class T>inline void read(T &x) {
x = 0; int f = 0; char ch = getchar();
while (!isdigit(ch)) f |= (ch == '-'), ch = getchar();
while (isdigit(ch)) x = x * 10 + ch - '0', ch = getchar();
x = f ? -x : x;
return ;
}
inline int get(int x) {
return t[t[x].fa].ch[0] == x ? 0 : 1;
}
inline void pushup(int x) {
t[x].sum = t[t[x].ch[0]].sum + t[t[x].ch[1]].sum + t[x].cnt;
}
inline void rotate(int x) {
int fa = t[x].fa, gfa = t[fa].fa;
int k = get(x);
t[x].fa = gfa;
t[gfa].ch[get(fa)] = x;
t[t[x].ch[k ^ 1]].fa = fa;
t[fa].ch[k] = t[x].ch[k ^ 1];
t[fa].fa = x;
t[x].ch[k ^ 1] = fa;
pushup(fa), pushup(x);
}
inline void splay(int x, int pos) {
while (t[x].fa != pos) {
int fa = t[x].fa, gfa = t[fa].fa;
if (gfa != pos) (t[fa].ch[0] == x) ^ (t[gfa].ch[0] == fa) ? rotate(x) : rotate(fa);
rotate(x);
}
if (pos == 0) root = x;
}
inline void find(int x) { //查找x的位置并旋转到根
int u = root;
if (!u) return ;
while (t[u].ch[x > t[u].val] && x != t[u].val) u = t[u].ch[x > t[u].val];
splay(u, 0);
}
inline void insert(int x) {
int u = root, fa = 0; //当前位置u,u的父节点ff
while (u && t[u].val != x) {
fa = u;
u = t[u].ch[x > t[u].val];
}
if (u) t[u].cnt++;
else {
u = ++tot;
if (fa) t[fa].ch[x > t[fa].val] = u; //如果父节点非根
t[u].ch[1] = t[u].ch[0] = 0; //没有儿子
t[u].fa = fa, t[u].val = x, t[u].cnt = 1, t[u].sum = 1;
}
splay(u, 0);
}
inline int nx(int x, int f) { //0 next;1 pre
find(x);
int u = root;
if (t[u].val > x && f) return u;
if (t[u].val < x && !f) return u;
u = t[u].ch[f]; //后继往左找,前驱往右找
while (t[u].ch[f ^ 1]) u = t[u].ch[f ^ 1];
return u;
}
inline int rank(int x) {
int u = root;
if (t[u].sum < x) return 0;
while (1) {
int v = t[u].ch[0];
if (x > t[v].sum + t[u].cnt) { //如果排名比左儿子的大小和当前节点的数量要大
x -= t[v].sum + t[u].cnt; //那么当前排名的数一定在右儿子上找
u = t[u].ch[1];
} else if (t[v].sum >= x) u = v;
else return t[u].val;
}
}
inline void Del(int x) {
int last = nx(x, 0), nxt = nx(x, 1);
splay(last, 0), splay(nxt, last);
int del = t[nxt].ch[0];
if (t[del].cnt > 1) {
t[del].cnt--;
splay(del, 0);
} else t[nxt].ch[0] = 0;
}
int main(int argc, char const *argv[]) {
insert(2147483647), insert(-2147483647);
read(n);
while (n --) {
int opt, k;
read(opt);
if (opt == 1) read(k), insert(k);
else if (opt == 2) read(k), Del(k);
else if (opt == 3) {
read(k);
find(k);
printf("%d\n", t[t[root].ch[0]].sum);
}
else if (opt == 4) {
read(k);
printf("%d\n", rank(k + 1));
}
else if (opt == 5) {
read(k);
printf("%d\n", t[nx(k, 0)].val);
}
else if (opt == 6) {
read(k);
printf("%d\n", t[nx(k, 1)].val);
}
}
return 0;
}




