算法刷题

1.生成100个随机数，要求随机数始终为4位数

public class test {
    public static void main(String[] args){
        Random random=new Random();
        StringBuffer sb=new StringBuffer();
        for (int i = 0; i <100 ; i++) {
            int num=random.nextInt(9999);//产生的随机数范围[0,9999)
            String stringnum=num+"";//转换成字符串类型
              for (int j = 0; j <4- stringnum.length(); j++) {
                  sb.append("0");
              }//对生成的随机数未满足4位的进行补0
            stringnum=sb.toString()+stringnum;
            System.out.println(stringnum);
            sb.delete(0,sb.length());//将sb清零，生成下一个随机数，再用
        }
    }
}

2.栈（stack）

Stack<> stack=new Stack<>();

pop( )----出栈（返回栈顶元素，且在堆栈中删除）
peek( )----（返回栈顶元素，但不在堆栈中删除）
push( 值)-----入栈，返回这个插入元素，也就是栈顶元素
add(值)-----插入元素，也就是栈顶元素，但是返回的是布尔值
add是继承自Vector的方法，返回值类型是boolean。

push是Stack自身的方法，返回值类型是参数类类型。
size()------返回栈的大小（里面存放的数据长度）

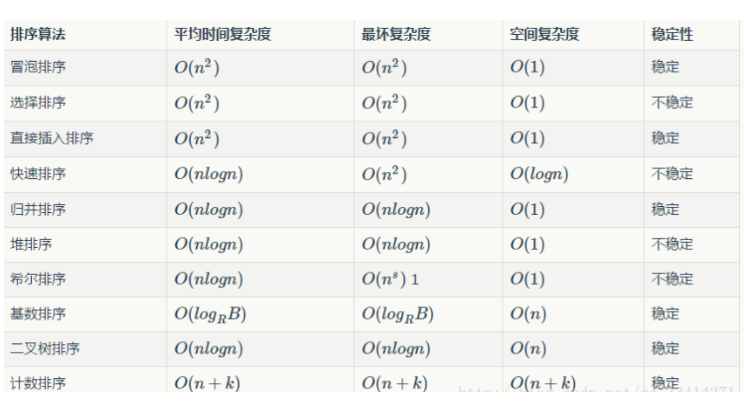
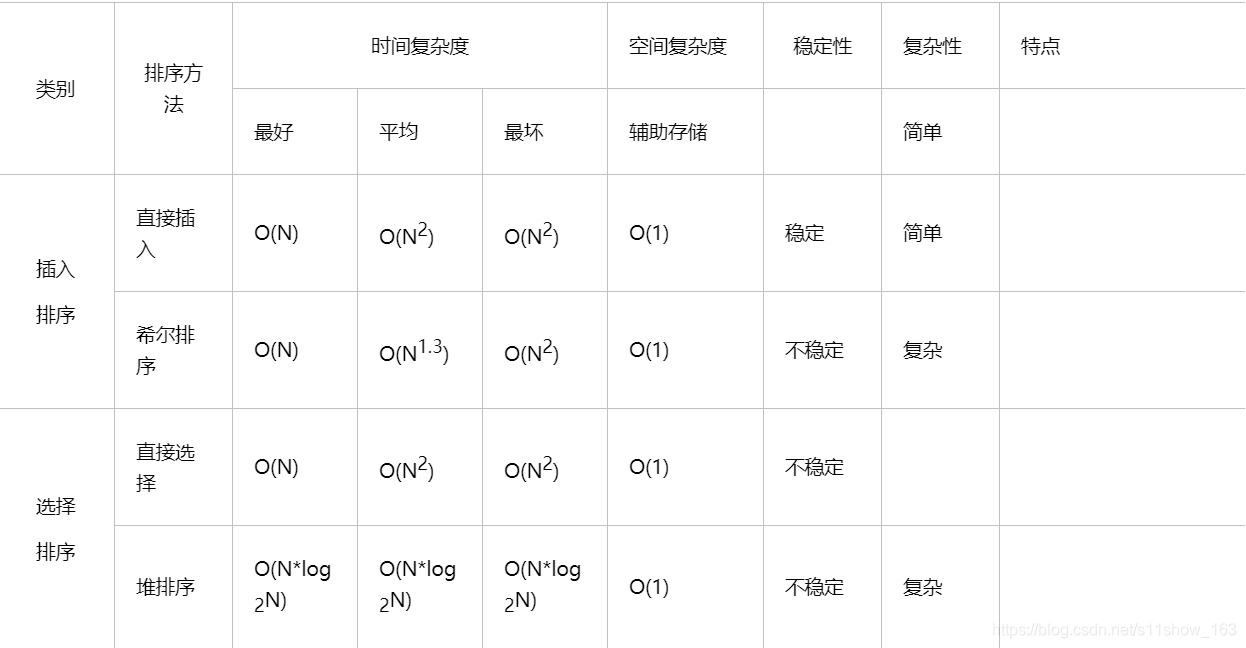
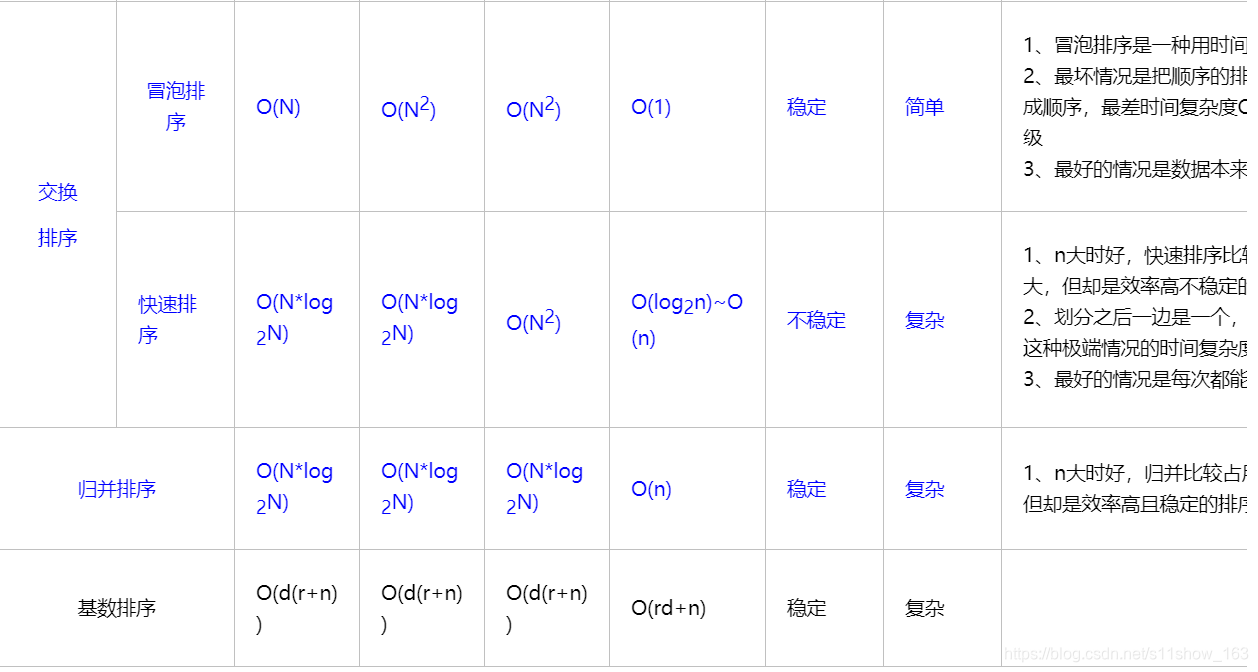
3.算法复杂度

O(1)就是最低的时空复杂度了，也就是耗时/耗空间与输入数据大小无关，无论输入数据增大多少倍，耗时/耗空间都不变。哈希算法就是典型的O(1)时间复杂度，无论数据规模多大，都可以在一次计算后找到目标（不考虑冲突的话）
时间复杂度为O(n)，就代表数据量增大几倍，耗时也增大几倍。比如常见的遍历算法。
再比如时间复杂度O(n^{2)，就代表数据量增大n倍时，耗时增大n的平方倍，这是比线性更高的时间复杂度。比如冒泡排序，就是典型的O(n}2)的算法，对n个数排序，需要扫描n×n次。

算法复杂度

在这里插入图片描述

当然在最坏的情况下，仍可能是相邻的两个数进行了交换。因此快速排序的最差时间复杂度和冒泡排序是一样的都是O(n^2)，它的平均时间复杂度为 O(nlogn)
解决：1.选取随机数作为枢
- 选取最后一个数：如果是一个已经排好序的数组，每次找到位置之后，左边是要进行排序的部分，数组长度是原长度-1，它的时间复杂度就是O(N^2)；如果每次找到的数都是中间的位置，它的时间复杂度就只有O(logN)
- 然而以随机数作为选取的标准num的时候，因为是随机的，就只能通过数学期望去计算它的时间复杂度，时间复杂度是O(logN)
2.使用左端，右端和中心的中值做为枢轴元

3.每次选取数据集中的中位数做枢轴。

//直接插入法---一直与前面的数做比较，如果后面小于前面，交换位置
     public void cr(int a[],int n){
    	 for(int i=0;i<n;i++){
    		 int j=i-1;
    		 int temp=a[i];
             //这是我们找出规律1
    		 while(j>=0 && temp<a[j]){
                 //temp不断地一直与前面的数a【j】作比较。这是规律3
    			 a[j+1]=a[j];
    			 j--;
    		 }
    		 a[j+1]=temp;
             //当temp>a【j】时，就把temp插入到a【j+1】里。这是规律4
    	 }
//快排---选择一个基准数，分区过程，将比这个数大的数全放到它的右边，小于或等于它的数全放到它的左边。再对左右区间重复第二步，直到各区间只有一个数。
public class QuickSort {
    public static void quickSort(int[] arr,int low,int high){
        int i,j,temp,t;
        if(low>high){
            return;
        }
        i=low;
        j=high;
        //temp就是基准位
        temp = arr[low]; 
        while (i<j) {
            //先看右边，依次往左递减
            while (temp<=arr[j]&&i<j) {
                j--;
            }
            //再看左边，依次往右递增
            while (temp>=arr[i]&&i<j) {
                i++;
            }
            //如果满足条件则交换
            if (i<j) {
                t = arr[j];
                arr[j] = arr[i];
                arr[i] = t;
            }
        }
        //最后将基准为与i和j相等位置的数字交换
         arr[low] = arr[i];
         arr[i] = temp;
        //递归调用左半数组
        quickSort(arr, low, j-1);
        //递归调用右半数组
        quickSort(arr, j+1, high);
    }
 
    public static void main(String[] args){
        int[] arr = {10,7,2,4,7,62,3,4,2,1,8,9,19};
        quickSort(arr, 0, arr.length-1);
        for (int i = 0; i < arr.length; i++) {
            System.out.println(arr[i]);
        }
    }
}
//冒泡排序：
         public static void ArraySortTest() {
		int[] ages= {21,27,31,19,50,32,16,25};
		System.out.println(Arrays.toString(ages));
		//控制比较轮数
		for(int i=1;i<ages.length;i++) {
			//每轮比较多少
			for(int j=0;j<ages.length-i;j++) {
				if(ages[j]>ages[j+1]) {
					int tmp=0;
					tmp=ages[j];
					ages[j]=ages[j+1];
					ages[j+1]=tmp;					
				}
			}
		}
		System.out.println(Arrays.toString(ages));
	}
//直接选择排序，每次选最小的放到最前 
    public static void choiceSort(int[] arr){  
          
        if(arr == null || arr.length < 1){  
            return;  
        }  
        int min = 0;  
        int temp;  
        /*只需要进行 n - 1 轮选择*/  
        for(int i = 0;i<arr.length - 1;i++){  
            min = i;                    //初始化当前最小的  
            for(int j = i + 1;j<arr.length;j++){  
                if(arr[min] > arr[j]){  
                    min=j;                //记住最小元素下标  
                }        
            }     
            //一轮后，当最小元素的下标不为i时交换位置  
            if(min != i){  
                temp = arr[i];  
                arr[i] = arr[min];  
                arr[min] = temp;  
            }  
        }    
    }  
//大顶堆排序
         
public class HeapSort1 {
 
    public static void main(String[] args) {
        int[] a = new int[]{16, 25, 7, 32, 6, 9};
        heapSort(a);
        System.out.println(Arrays.toString(a));
    }
 
    /**
     * 构造大顶堆
     * @param arr 待调整数组
     * @param size 调整多少
     * @param index 调整哪一个 最后一个叶子节点的父节点开始调整
     */
    public static void maxHeap(int arr[], int size, int index) {
 
        //左子节点
        int leftNode = 2 * index + 1;
        //右子节点
        int rightNode = 2 * index + 2;
 
        int max = index;//假设自己最大
 
        //分别比较左右叶子节点找出最大
        if(leftNode < size && arr[leftNode] > arr[max]) {//如果左侧叶子节点大于max则将最大位置换成leftNode并且递归需要限定范围为数组长度，
            max = leftNode;//将最大位置改为左子节点
        }
 
        if(rightNode < size && arr[rightNode] > arr[max]) {//如果左侧叶子节点大于max则将最大位置换成rightNode
            max = rightNode;//将最大位置改为右子节点
        }
 
        //如果不相等就需要交换
        if(max != index) {
            int tem = arr[index];
            arr[index] = arr[max];
            arr[max] = tem;
            //如果下边还有叶子节点并且破坏了原有的堆。需要重新调整
            maxHeap(arr, size, max);//位置为刚才改动的位置；
        }
    }
 
    /**
     * 需要将最大的顶部与最后一个交换
     * @param arr
     */
    public static void heapSort(int arr[]) {
        int start = (arr.length - 1)/2;//开始位置最后一个非叶子节点，最后一个叶子节点的父节点
        for(int i = start; i>=0; i--) {
            maxHeap(arr, arr.length, i);
        }
 
        //最后一个跟第一个进行调整
        for(int i = arr.length-1; i>0; i--) {//因为数组从零开始的，所以最后一个是数组长度减一
            int temp = arr[0];//最前面的一个
            arr[0] = arr[i];//最后一个
            arr[i] = temp;
            //调整后再进行大顶堆调整
            maxHeap(arr, i, 0);
        }
    }
}
————————————————
版权声明：本文为CSDN博主「ccmedu」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/ccmedu/article/details/90247077

4.哈希

pairs.containsKey(ch)//查看ch是不是pairs集合的key值
pairs.get(ch)//获得ch在pairs集合中的value值

5.树

为什么叫前序、后序、中序？
一棵二叉树由根结点、左子树和右子树三部分组成，若规定 D、L、R 分别代表遍历根结点、遍历左子树、遍历右子树，则二叉树的遍历方式有 6 种：DLR、DRL、LDR、LRD、RDL、RLD。由于先遍历左子树和先遍历右子树在算法设计上没有本质区别，所以，只讨论三种方式：

DLR--前序遍历（根在前，从左往右，一棵树的根永远在左子树前面，左子树又永远在右子树前面）

LDR--中序遍历（根在中，从左往右，一棵树的左子树永远在根前面，根永远在右子树前面）

LRD--后序遍历（根在后，从左往右，一棵树的左子树永远在右子树前面，右子树永远在根前面）

前、中、后序遍历：https://blog.csdn.net/abcdef314159/article/details/106466456?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522161534467016780255239273%2522%252C%2522scm%2522%253A%252220140713.130102334..%2522%257D&request_id=161534467016780255239273&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2_allsobaiduend~default-1-106466456.first_rank_v2_pc_rank_v29&utm_term=java%E4%BA%8C%E5%8F%89%E6%A0%91%E9%81%8D%E5%8E%86%E7%AE%97%E6%B3%95

6.Linkedlist

offer，add区别：

一些队列有大小限制，因此如果想在一个满的队列中加入一个新项，多出的项就会被拒绝。

这时新的 offer 方法就可以起作用了。它不是对调用 add() 方法抛出一个 unchecked 异常，而只是得到由 offer() 返回的 false。

poll，remove区别：

remove() 和 poll() 方法都是从队列中删除第一个元素。remove() 的行为与 Collection 接口的版本相似，

但是新的 poll() 方法在用空集合调用时不是抛出异常，只是返回 null。因此新的方法更适合容易出现异常条件的情况。

，element区别：

element() 和 peek() 用于在队列的头部查询元素。与 remove() 方法类似，在队列为空时， element() 抛出一个异常，而 peek() 返回 null

7.链表，双指针

 public class ListNode {
      int val;
      ListNode next;
      ListNode(int x) { val = x; }
  }
public List
 ListNode former=head.next;
 ListNode latter=head;

posted @ 2021-05-05 13:49 维他命D片阅读(74) 评论(0) 编辑收藏举报

刷新页面返回顶部

维他命D片