「树链剖分」 学习笔记
一,树链剖分的思想与概述
正如其名,树链剖分用于将树剖分成若干条链的形式,以维护树上路径的信息,其中剖分出的链有多种形式,最常见的是重链,还有长链或更多其它的链。
其中剖分出的链为重链时,就引出了下文的主角「重链剖分」。
重链剖分能保证划分出的每条重链上的节点 DFS 序连续,因此可以用一些维护序列的数据结构(如线段树,树状数组等)来维护树上路径的信息。
没学过线段树的出门左转题库搜索线段树模板 1。
二,重链剖分
- 定义
-
重儿子:表示其子节点中子树大小最大的节点。(多个点大小同时最大取任意一个)
-
轻儿子:除重儿子外的其它所有子节点。
-
重边:非叶子结点到它的重儿子的边。
-
轻边:非叶子结点到它的轻儿子的边。
-
重链:若干条首尾连接的重边构成的链。
-
链首:每条重链中深度最小的点。
-
重边优先遍历:DFS 遍历树时,优先遍历重边,其余同深度优先遍历。
其中,我们把把落单的结点也当作一条重链,那么整棵树就会被剖分成若干条重链。
如图:
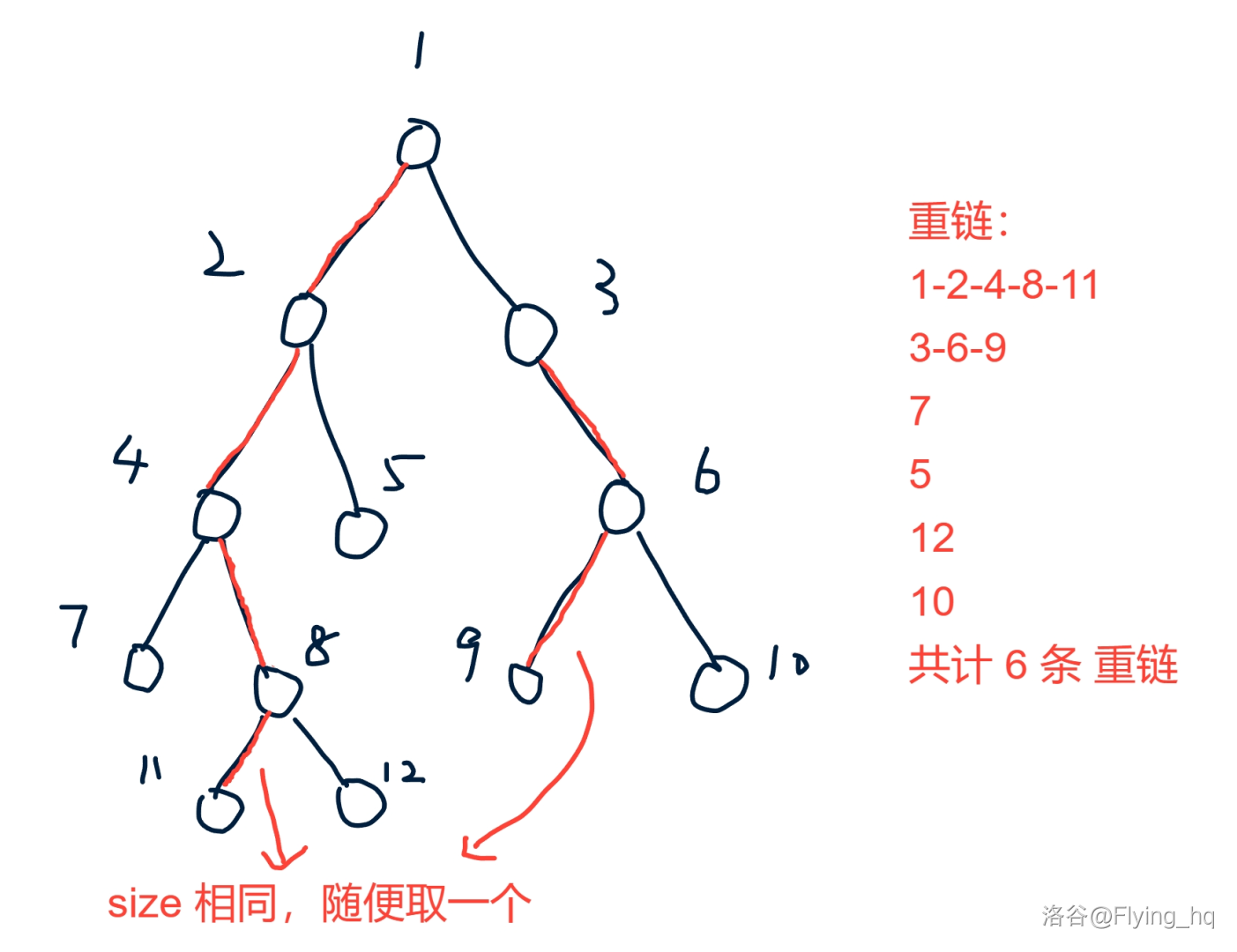
- 实现
分两个 DFS,第一个 DFS 求出所有节点的
我们钦定根节点的深度为 0。
int fa[N], sz[N], dep[N], son[N];//上文所提的 4 个数组
void dfs1(int u, int f){
sz[u] = 1;
for (int i = pre[u]; i; i = e[i].next){//这里用的是链式前向星,也可以用 vector,看个人习惯
int v = e[i].to;
if (v == f) continue;//fa 和自己之间来回走(死循环)
fa[v] = u;//记录 fa
dep[v] = dep[u] + 1;//记录 dep
dfs1(v, u);//DFS 得到 v 的 size
sz[u] += sz[v];//记录 u 的 size
if (sz[v] > sz[son[u]]) son[u] = v;//如果 v 的 size 大于原本 u 的重儿子的 size,更新 u 的重儿子为 v,其中 son 数组初始化为 0
}
}
int pos;//DFS 序的序号
int top[N], tid[N];
void dfs2(int u, int x){
top[u] = x;//链首
tid[u] = ++pos;//DFS 序
if (son[u]) dfs2(son[u], x);//有重儿子,优先遍历重儿子,链首还是为 x
for (int i = pre[u]; i; i = e[i].next){
int v = e[i].to;
if (v == fa[u]) continue;
if (v == son[u]) continue;
dfs2(v, v);//自己单成一条重链,链首为自己
}
}
- 性质
- 性质 1:树上每个节点都属于且仅属于一条重链。
反证法:
假设 1:点
即点
假设 2:点
首先点
- 点
- 点
综上,命题得证。
- 性质 2:
令
假设
由于
命题得证。
- 应用:
没有什么用的前置铺垫,树链剖分求 LCA:
不断向上跳重链,当跳到同一条重链上时,深度较小的结点即为 LCA。
向上跳重链时需要先跳所在重链链首深度较大的那个。
int lca(int u, int v){
while(top[u] != top[v]){
if (dep[top[u]] > dep[top[v]]) u = fa[top[u]];
else v = fa[top[v]];
}
return dep[u] < dep[v] ? u : v;
}
十分简单,下面看例题:
P2590 [ZJOI2008] 树的统计:
根据题目内容,发现你的线段树需要维护三种操作。
-
单点修改某个节点的权值。
-
查询
-
查询
单点修改很容易实现,问题是如何查询两个节点之间的路径的一些信息。
考虑是如何用倍增求 LCA 的。首先我们将两个节点提到同一高度,然后将两个节点一起向上跳,对于树链剖分也可以使用这样的思想。
在向上跳的过程中,将当前节点向上跳到重链链首,如果该节点已经是链首,向上跳一个节点,直到两个节点相同,顺手查询区间信息。
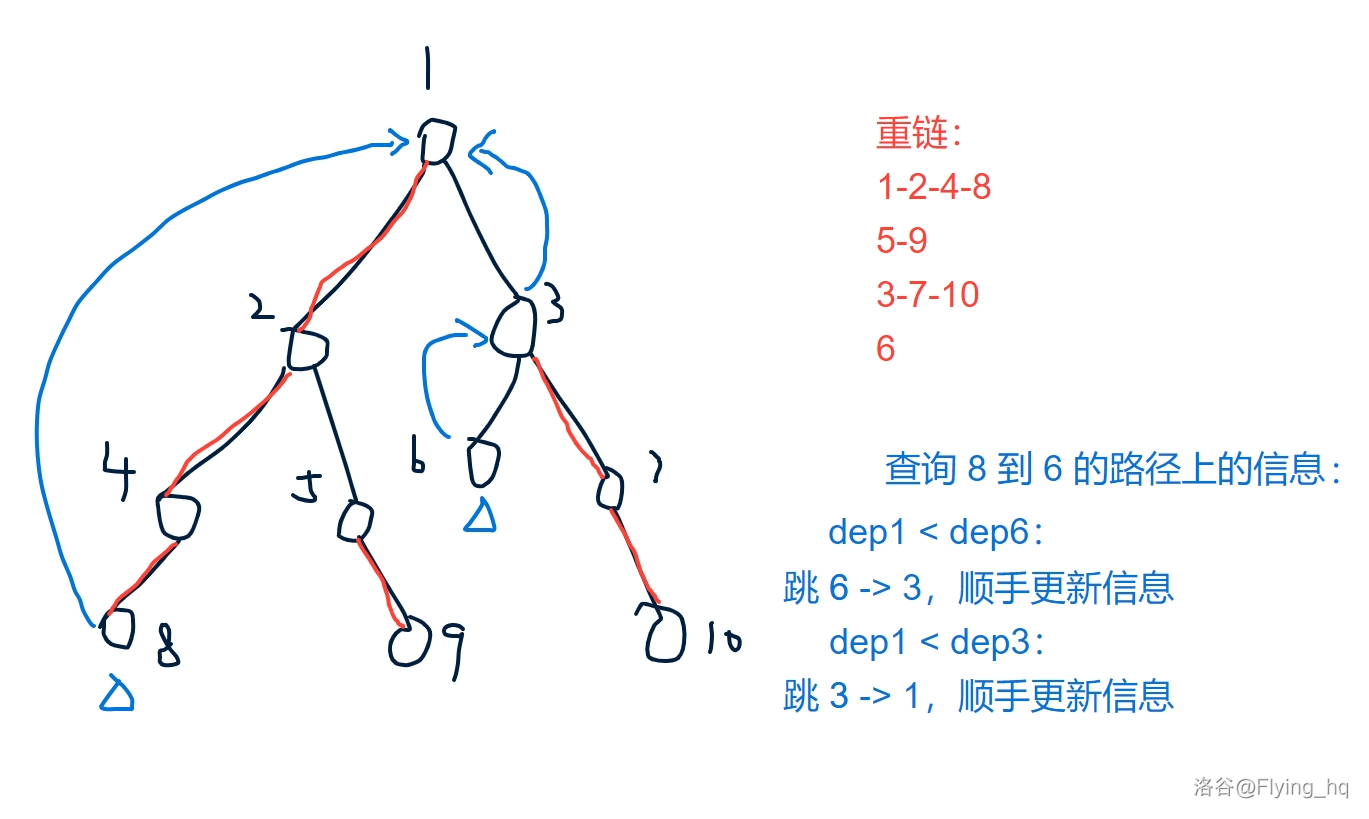
代码实现:
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N = 2e5 + 5, inf = 1e9 + 7;
int n, a[N];
struct asdf{
int to, next;
}e[N << 1];
int pre[N], k;
void add(int u, int v){
e[++k] = {v, pre[u]};
pre[u] = k;
}
struct Segment_Tree{
struct node{
int v, add, s;//v 是最大值,s 是和,add 是懒标记
}t[N << 1];
//以下是不想解释的线段树
void pushup(int k){
t[k].v = max(t[k << 1].v, t[k << 1 | 1].v);
t[k].s = t[k << 1].s + t[k << 1 | 1].s;
}
void pushdown(int k, int l, int r){
if (t[k].add){
t[k << 1].v = t[k << 1 | 1].v = t[k << 1].add = t[k << 1 | 1].add = t[k].add;
int mid = (l + r) >> 1;
t[k << 1].s = 1ll * (mid - l + 1) * t[k].add;
t[k << 1 | 1].s = 1ll * (r - mid) * t[k].add;
t[k].add = 0;
}
}
void build(int k, int l, int r){
t[k].add = 0;
if (l == r){
t[k].v = t[k].s = a[l];
return ;
}
int mid = (l + r) >> 1;
build(k << 1, l, mid);
build(k << 1 | 1, mid + 1, r);
pushup(k);
}
void change(int k, int l, int r, int x, int y, int v){
if (r < x || l > y) return ;
if (l >= x && r <= y){
t[k].add = t[k].v = v;
t[k].s = 1ll * (r - l + 1) * v;
return ;
}
int mid = (l + r) >> 1;
pushdown(k, l, r);
change(k << 1, l, mid, x, y, v);
change(k << 1 | 1, mid + 1, r, x, y, v);
pushup(k);
}
int ask(int k, int l, int r, int x, int y){
if (l >= x && r <= y) return t[k].v;
int ans = -inf, mid = (l + r) >> 1;
pushdown(k, l, r);
if (x <= mid) ans = max(ans, ask(k << 1, l, mid, x, y));
if (y >= mid + 1) ans = max(ans, ask(k << 1 | 1, mid + 1, r, x, y));
return ans;
}
int ask2(int k, int l, int r, int x, int y){
if (l >= x && r <= y) return t[k].s;
int ans = 0, mid = (l + r) >> 1;
pushdown(k, l, r);
if (x <= mid) ans += ask2(k << 1, l, mid, x, y);
if (y >= mid + 1) ans += ask2(k << 1 | 1, mid + 1, r, x, y);
return ans;
}
//以上是不想解释的线段树
}chain;
//以下是不想解释的已经讲过的 dfs
int fa[N], sz[N], top[N], tid[N], dep[N], son[N];
int l[N];
void dfs1(int u, int f){
sz[u] = 1;
for (int i = pre[u]; i; i = e[i].next){
int v = e[i].to;
if (v == f) continue;
fa[v] = u;
dep[v] = dep[u] + 1;
dfs1(v, u);
sz[u] += sz[v];
if (sz[v] > sz[son[u]]) son[u] = v;
}
}
int pos;
void dfs2(int u, int x){
top[u] = x;
tid[u] = ++pos;
a[pos] = l[u];
if (son[u]) dfs2(son[u], x);
for (int i = pre[u]; i; i = e[i].next){
int v = e[i].to;
if (v == fa[u]) continue;
if (v == son[u]) continue;
dfs2(v, v);
}
}
//以上是不想解释的已经讲过的 dfs
int query(int u, int v){
int val = -inf, tu = top[u], tv = top[v];//取出 u 和 v 的链首
while(tu != tv){//一直跳,直到在一条重链上
if (dep[tu] < dep[tv]){//取深度更深的点进行更新
swap(u, v);
swap(tu, tv);
}
val = max(val, chain.ask(1, 1, n, tid[tu], tid[u]));//获取 u 到 链首的信息
u = fa[tu], tu = top[u];//往上跳
}
if (tid[u] > tid[v]) swap(u, v);//也是取深度更深的点更新,换了种方式,可以感性理解题解一下
val = max(val, chain.ask(1, 1, n, tid[u], tid[v]));//更新最大值
return val;
}
int sum(int u, int v){//同上,改成了求和而已
int val = 0, tu = top[u], tv = top[v];
while(tu != tv){
if (dep[tu] < dep[tv]){
swap(u, v);
swap(tu, tv);
}
val += chain.ask2(1, 1, n, tid[tu], tid[u]);
u = fa[tu], tu = top[u];
}
if (tid[u] > tid[v]) swap(u, v);
val += chain.ask2(1, 1, n, tid[u], tid[v]);
return val;
}
signed main(){
cin >> n;
for (int i = 1; i <= n - 1; i++){
int u, v;
scanf("%lld %lld", &u, &v);
add(u, v), add(v, u);//建边
}
for (int i = 1; i <= n; i++) cin >> l[i];//点权
dfs1(1, 0);//预处理
dfs2(1, 1);//剖分
chain.build(1, 1, n);//建维护剖分的线段的线段树
int q;
cin >> q;
while(q--){
string s;
int x, y;
cin >> s >> x >> y;
if (s[0] == 'Q'){
if (s[1] == 'M') cout << query(x, y) << "\n";//和
else cout << sum(x, y) << "\n";//最大值
}
else{
chain.change(1, 1, n, tid[x], tid[x], y);//单点修改
}
}
return 0;
}
P4114 Qtree1:
和上题没有多大的不一样的地方,只是把维护点权变成了维护边权,将
代码实现:
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N = 1e6 + 5;
int n, a[N];
struct asdf{
int to, next, len;
}e[N << 1];
int pre[N], k;
void add(int u, int v, int w){
e[++k] = {v, pre[u], w};
pre[u] = k;
}
struct Segment_Tree{
struct node{
int v, add;//v 表示最大值
}t[N << 1];
//以下是仍然不想解释的线段树
void pushup(int k){
t[k].v = max(t[k << 1].v, t[k << 1 | 1].v);
}
void pushdown(int k){
if (t[k].add){
t[k << 1].v = t[k << 1 | 1].v = t[k << 1].add = t[k << 1 | 1].add = t[k].add;
t[k].add = 0;
}
}
void build(int k, int l, int r){
t[k].add = 0;
if (l == r){
t[k].v = a[l];
return ;
}
int mid = (l + r) >> 1;
build(k << 1, l, mid);
build(k << 1 | 1, mid + 1, r);
pushup(k);
}
void change(int k, int l, int r, int x, int y, int v){
if (r < x || l > y) return ;
if (l >= x && r <= y){
t[k].add = t[k].v = v;
return ;
}
int mid = l + r >> 1;
pushdown(k);
change(k << 1, l, mid, x, y, v);
change(k << 1 | 1, mid + 1, r, x, y, v);
pushup(k);
}
int ask(int k, int l, int r, int x, int y){
if (l >= x && r <= y) return t[k].v;
int ans = 0, mid = (l + r) >> 1;
pushdown(k);
if (x <= mid) ans = max(ans, ask(k << 1, l, mid, x, y));
if (y >= mid + 1) ans = max(ans, ask(k << 1 | 1, mid + 1, r, x, y));
return ans;
}
//以上是仍然不想解释的线段树
}chain;
//以下是仍然不想解释的 DFS
int fa[N], sz[N], top[N], tid[N], dep[N], son[N], l[N];
void dfs1(int u, int f){
sz[u] = 1;
for (int i = pre[u]; i; i = e[i].next){
int v = e[i].to;
if (v == f) continue;
fa[v] = u;
dep[v] = dep[u] + 1;
l[v] = e[i].len;//这里说一下,边权转点权
dfs1(v, u);
sz[u] += sz[v];
if (sz[v] > sz[son[u]]) son[u] = v;
}
}
int pos;
void dfs2(int u, int x){
top[u] = x;
tid[u] = ++pos;
a[pos] = l[u];//这里再说一下,边权转点权
if (son[u]) dfs2(son[u], x);
for (int i = pre[u]; i; i = e[i].next){
int v = e[i].to;
if (v == fa[u]) continue;
if (v == son[u]) continue;
dfs2(v, v);
}
}
//以上是仍然不想解释的 DFS
//以下是不想解释的区间查询
int query(int u, int v){
int val = 0, tu = top[u], tv = top[v];
while(tu != tv){
if (dep[tu] < dep[tv]){
swap(u, v);
swap(tu, tv);
}
val = max(val, chain.ask(1, 1, n, tid[tu], tid[u]));
u = fa[tu], tu = top[u];
}
if (tid[u] > tid[v]) swap(u, v);
val = max(val, chain.ask(1, 1, n, tid[u] + 1, tid[v]));
return val;
}
//以上是不想解释的区间查询
signed main(){
cin >> n;
for (int i = 1; i <= n - 1; i++){
int u, v, w;
scanf("%lld %lld %lld", &u, &v, &w);
add(u, v, w), add(v, u, w);//建边
}
dfs1(1, 0);
dfs2(1, 1);
chain.build(1, 1, n);
while(1){
string s;
cin >> s;
if (s == "DONE") break;
if (s == "QUERY"){
int u, v;
cin >> u >> v;
if (u == v) puts("0");//如题意
else cout << query(u, v) << "\n";//查询
}
else{
int u, t;
cin >> u >> t;
if (dep[e[u * 2].to] > dep[e[u * 2 - 1].to]) u = e[u * 2].to;//得到边 u 所对应的点
else u = e[u * 2 - 1].to;//同上
chain.change(1, 1, n, tid[u], tid[u], t);//单点修改(即使我写的是区间修改)
}
}
return 0;
}
P3038 [USACO11DEC] Grass Planting G:
同 P4114,需要将边权转化为点权,然后变成了区间修改,单点查询,因为我懒得改代码所以写的是区间查询()。
代码实现:
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N = 1e6 + 5;
int n, m, a[N];
struct asdf{
int to, next, len;
}e[N << 1];
int pre[N], k;
void add(int u, int v, int w){
e[++k] = {v, pre[u], w};
pre[u] = k;
}
//以下是不想解释的线段树
struct Segment_Tree{
struct node{
int v, add;
}t[N << 1];
void pushup(int k){
t[k].v = max(t[k << 1].v, t[k << 1 | 1].v);
}
void pushdown(int k){
if (t[k].add){
t[k << 1].v += t[k].add;
t[k << 1 | 1].v += t[k].add;
t[k << 1].add += t[k].add;
t[k << 1 | 1].add += t[k].add;
t[k].add = 0;
}
}
void build(int k, int l, int r){
t[k].add = 0;
if (l == r){
t[k].v = a[l];
return ;
}
int mid = (l + r) >> 1;
build(k << 1, l, mid);
build(k << 1 | 1, mid + 1, r);
pushup(k);
}
void change(int k, int l, int r, int x, int y, int v){
if (r < x || l > y) return ;
if (l >= x && r <= y){
t[k].add += v;
t[k].v += v;
return ;
}
int mid = l + r >> 1;
pushdown(k);
change(k << 1, l, mid, x, y, v);
change(k << 1 | 1, mid + 1, r, x, y, v);
pushup(k);
}
int ask(int k, int l, int r, int x, int y){
if (r < x || l > y) return 0;
if (l >= x && r <= y) return t[k].v;
int mid = (l + r) >> 1;
pushdown(k);
return max(ask(k << 1, l, mid, x, y), ask(k << 1 | 1, mid + 1, r, x, y));
}
}chain;
//以上是不想解释的线段树
//以下是不想解释的 DFS
int fa[N], sz[N], top[N], tid[N], dep[N], son[N], l[N];
void dfs1(int u, int f){
sz[u] = 1;
for (int i = pre[u]; i; i = e[i].next){
int v = e[i].to;
if (v == f) continue;
fa[v] = u;
dep[v] = dep[u] + 1;
l[v] = e[i].len;
dfs1(v, u);
sz[u] += sz[v];
if (sz[v] > sz[son[u]]) son[u] = v;
}
}
int pos;
void dfs2(int u, int x){
top[u] = x;
tid[u] = ++pos;
a[pos] = l[u];
if (son[u]) dfs2(son[u], x);
for (int i = pre[u]; i; i = e[i].next){
int v = e[i].to;
if (v == fa[u]) continue;
if (v == son[u]) continue;
dfs2(v, v);
}
}
//以上是不想解释的 DFS
//以下是不想解释的区查
int query(int u, int v){
int val = 0, tu = top[u], tv = top[v];
while(tu != tv){
if (dep[tu] < dep[tv]){
swap(u, v);
swap(tu, tv);
}
val = max(val, chain.ask(1, 1, n, tid[tu], tid[u]));
u = fa[tu], tu = top[u];
}
if (tid[u] > tid[v]) swap(u, v);
val = max(val, chain.ask(1, 1, n, tid[u] + 1, tid[v]));
return val;
}
//以上是不想解释的区查
void update(int u, int v){
int tu = top[u], tv = top[v];//得到链首
while(tu != tv){
if (dep[tu] < dep[tv]){//选更深的跳
swap(u, v);
swap(tu, tv);
}
chain.change(1, 1, n, tid[tu], tid[u], 1);//修改
u = fa[tu], tu = top[u];//跳就完事了
}
if (tid[u] > tid[v]) swap(u, v);//选更深的
chain.change(1, 1, n, tid[u] + 1, tid[v], 1);//避开点 u,因为将边权转为了点权
}
//以下是不想解释的主函数
signed main(){
cin >> n >> m;
for (int i = 1; i <= n - 1; i++){
int u, v;
scanf("%lld %lld", &u, &v);
add(u, v, 1), add(v, u, 1);
}
dfs1(1, 0);
dfs2(1, 1);
chain.build(1, 1, n);
while(m--){
string s;
cin >> s;
if (s == "Q"){
int u, v;
cin >> u >> v;
if (fa[u] == v) cout << chain.ask(1, 1, n, tid[u], tid[u]) - 1 << "\n";
else if (fa[v] == u) cout << chain.ask(1, 1, n, tid[v], tid[v]) - 1 << "\n";
}
else{
int u, v;
cin >> u >> v;
update(u, v);
}
}
return 0;
}
//以上是不想解释的主函数
P3384 【模板】重链剖分/树链剖分:
啥,你问我为什么做了三道题才到模板题?
沉思.jpg。
哦,因为这题里又多了两个操作,且修改和查询操作都是区间的,所以放后面点。
多了取模和子树操作,取模好解决,子树操作怎么办?
因为每个子树的
代码实现:
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N = 2e5 + 5, inf = 1e9 + 7;
int n, m, r, p, a[N];
struct asdf{
int to, next;
}e[N << 1];
int pre[N], k;
void add(int u, int v){
e[++k] = {v, pre[u]};
pre[u] = k;
}
struct Segment_Tree{
struct node{
int add, s;
}t[N << 1];
void pushup(int k){
t[k].s = t[k << 1].s + t[k << 1 | 1].s;
t[k].s %= p;
}
void pushdown(int k, int l, int r){
if (t[k].add){
t[k << 1].add = (t[k << 1].add + t[k].add) % p;
t[k << 1 | 1].add = (t[k << 1 | 1].add + t[k].add) % p;
int mid = (l + r) >> 1;
t[k << 1].s = (t[k << 1].s + 1ll * (mid - l + 1) * t[k].add % p) % p;
t[k << 1 | 1].s = (t[k << 1 | 1].s + 1ll * (r - mid) * t[k].add % p) % p;
t[k].add = 0;
}
}
void build(int k, int l, int r){
t[k].add = 0;
if (l == r){
t[k].s = a[l];
return ;
}
int mid = (l + r) >> 1;
build(k << 1, l, mid);
build(k << 1 | 1, mid + 1, r);
pushup(k);
}
void change(int k, int l, int r, int x, int y, int v){
if (r < x || l > y) return ;
if (l >= x && r <= y){
t[k].add = (t[k].add + v) % p;
t[k].s = (t[k].s + 1ll * (r - l + 1) * v % p) % p;
return ;
}
int mid = (l + r) >> 1;
pushdown(k, l, r);
change(k << 1, l, mid, x, y, v);
change(k << 1 | 1, mid + 1, r, x, y, v);
pushup(k);
}
int ask(int k, int l, int r, int x, int y){
if (l >= x && r <= y) return t[k].s % p;
int ans = 0, mid = (l + r) >> 1;
pushdown(k, l, r);
if (x <= mid) ans = (ans + ask(k << 1, l, mid, x, y)) % p;
if (y >= mid + 1) ans = (ans + ask(k << 1 | 1, mid + 1, r, x, y)) % p;
return ans % p;
}
}chain;
int fa[N], sz[N], top[N], tid[N], dep[N], son[N];
int l[N];
void dfs1(int u, int f){
sz[u] = 1;
for (int i = pre[u]; i; i = e[i].next){
int v = e[i].to;
if (v == f) continue;
fa[v] = u;
dep[v] = dep[u] + 1;
dfs1(v, u);
sz[u] += sz[v];
if (sz[v] > sz[son[u]]) son[u] = v;
}
}
int pos;
void dfs2(int u, int x){
top[u] = x;
tid[u] = ++pos;
a[pos] = l[u];
if (son[u]) dfs2(son[u], x);
for (int i = pre[u]; i; i = e[i].next){
int v = e[i].to;
if (v == fa[u]) continue;
if (v == son[u]) continue;
dfs2(v, v);
}
}
void update(int u, int v, int w){
w %= p;
int tu = top[u], tv = top[v];
while(tu != tv){
if (dep[tu] < dep[tv]){
swap(u, v);
swap(tu, tv);
}
chain.change(1, 1, n, tid[tu], tid[u], w);
u = fa[tu], tu = top[u];
}
if (tid[u] > tid[v]) swap(u, v);
chain.change(1, 1, n, tid[u], tid[v], w);
}
int query(int u, int v){
int val = 0, tu = top[u], tv = top[v];
while(tu != tv){
if (dep[tu] < dep[tv]){
swap(u, v);
swap(tu, tv);
}
val += chain.ask(1, 1, n, tid[tu], tid[u]);
u = fa[tu], tu = top[u];
}
if (tid[u] > tid[v]) swap(u, v);
val += chain.ask(1, 1, n, tid[u], tid[v]);
return val;
}
//以上全都不想解释了
signed main(){
cin >> n >> m >> r >> p;
for (int i = 1; i <= n; i++) cin >> l[i];
for (int i = 1; i <= n - 1; i++){
int u, v;
scanf("%lld %lld", &u, &v);
add(u, v), add(v, u);
}
dfs1(r, 0);
dfs2(r, r);
chain.build(1, 1, n);
while(m--){
int opt, x, y, z;
cin >> opt >> x;
if (opt == 1){
cin >> y >> z;
update(x, y, z);
}
else if (opt == 2){
cin >> y;
cout << query(x, y) % p << "\n";
}
else if (opt == 3){
cin >> y;
y %= p;
chain.change(1, 1, n, tid[x], tid[x] + sz[x] - 1, y);//子树操作,暴力修改
}
else{
cout << chain.ask(1, 1, n, tid[x], tid[x] + sz[x] - 1) % p << "\n";//子树操作,暴力查询
}
}
return 0;
}
想听的更详细点可以翻翻上面题目的题解。
思考题:P2486 [SDOI2011] 染色。
这里大致讲下思路,全部代码请读者自行实现。
就是多维护每个线段树节点的左端点颜色和右端点颜色,然后查询的时候时刻检查 lson 的右端点颜色和 rson 的左端点颜色是否一样,一样则将连续段数减一,重链剖分的查询同理。
三,尾声
终于没了,Markdown编辑界面已经较卡了,所以长链剖分咕到另一篇笔记里去吧。




【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 在鹅厂做java开发是什么体验
· 百万级群聊的设计实践
· WPF到Web的无缝过渡:英雄联盟客户端的OpenSilver迁移实战
· 永远不要相信用户的输入:从 SQL 注入攻防看输入验证的重要性
· 浏览器原生「磁吸」效果!Anchor Positioning 锚点定位神器解析