理论知识了解https://www.cnblogs.com/6dan_hust/archive/2010/08/23/1806560.html
有一农夫带一只狼、一只羊和一筐菜欲从河的左岸乘船到右岸，但受下列条件限制:
(1)船太小,农夫每次只能带一样东西过河;
(2)如果没有农夫看管，则狼要吃羊，羊要吃菜。
请用状态空间法设计一个过河方案，使得农夫、狼、羊、菜都能不受损失地过河。画出相应的状态空间图。
提示:
(1)用四元组(农夫、狼、羊、菜)表示状态，其中每个元素都可为0或1,用0表示在左岸，用1表示在右岸。
(2)把每次过河的一种安排作为一个算符，每次过河都必须有农夫，因为只有他可以划船。
解：状态用四元组表示为S（P，W，G，V），其中P为农民，W为狼，G为羊，V为菜，B为船，B=0为船在左岸，1为船在右岸。初始状态为S0=（0，0，0，0），目标状态为Sg=（1，1，1，1）。
安全规则：
1）不能将G与W单独留在对岸： not（W==G and P！=W）；
2）不能单独将G与V留在对岸：not（G==V and G！=P）
操作算符定义为：
P（S）仅农夫过河：if （安全） then {P（S），得到一个新状态（1-P，W，G，V）}；
PG（S）：农夫带羊过河：if （安全） then {PG（S），得到一个新状态（1-P，W，1-G，V）}；
PW（S）：农夫带狼过河：if （安全） then {PW（S），得到一个新状态（1-P，1-W，G，V）}；
PV（S）：农夫带菜过河：if（安全）then {PV（S），得到一个新状态（1-P，W，G，1-V）}。
解：
①分析状态
因为以S(P,W,G,V)的形式且P,W,G,V只有0,1两种取值，所以有2*2*2*2种状态
| 状态 | (P,W,G,V) | 状态 | (P,W,G,V) | 状态 | (P,W,G,V) | 状态 | (P,W,G,V) |
| S1 | (0,0,0,0) | S5 | (0,1,0,0) | S9 | (1,0,0,0) | S13 | (1,1,0,0) |
| S2 | (0,0,0,1) | S6 | (0,1,0,1) | S10 | (1,0,0,1) | S14 | (1,1,0,1) |
| S3 | (0,0,1,0) | S7 | (0,1,1,0) | S11 | (1,0,1,0) | S15 | (1,1,1,0) |
| S4 | (0,0,1,1) | S8 | (0,1,1,1) | S12 | (1,0,1,1) | S16 | (1,1,1,1) |
要求是从S1转换到S16。
②去掉不满足条件的状态
- 左岸，农民不在，狼羊，羊菜不能在一起，即（1,0,0，*），（1，*，0,0）
- 右岸，农民不在，狼羊，羊菜不能在一起，即（0,1,1，*），（0，*，1,1）
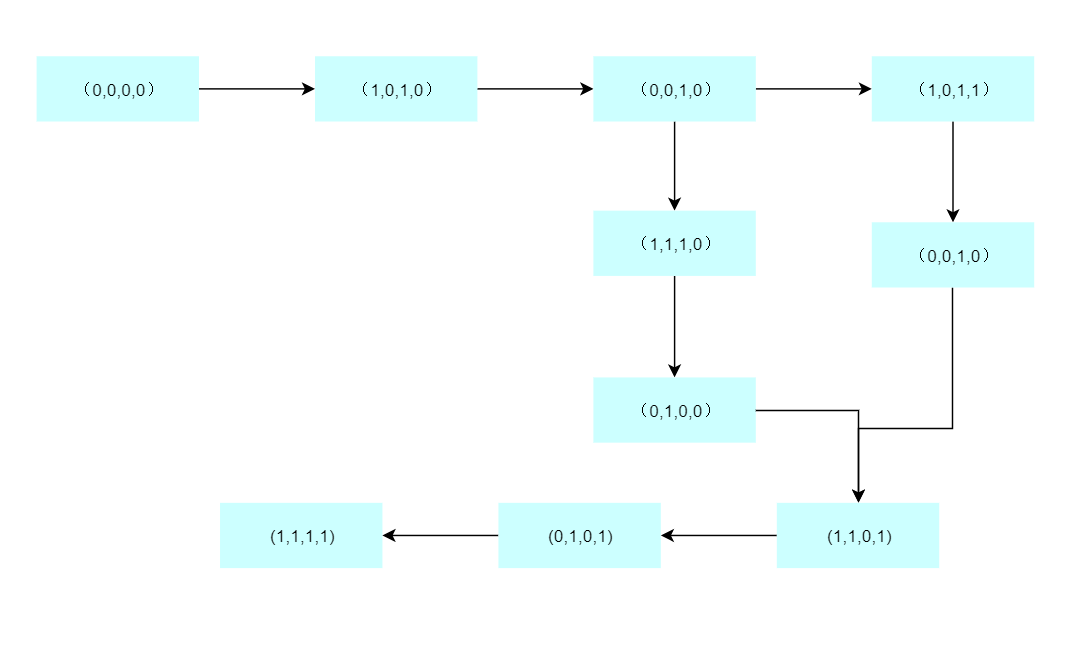
③绘制状态图
