史密斯圆图
的关于阻抗
阻抗分三种，电阻、电容、电感，三者阻抗表达式如下：
| 符号 | 单位 | 阻抗表达式 | 备注 | |
| 电阻 | R | 欧姆 Ω |  |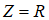
电压电流相位相同 |
| 电容 | C | 法拉 F |  |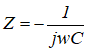
电压相位落后电流90度 |
| 电感 | L | 亨利 H |  |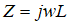
电压相位超前电流90度 |
| 阻抗 | Z | 欧姆 Ω |  |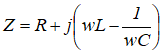
wL-1/wC < 0 称为容性负载 wL-1/wC > 0 称为感性负载 |
在具有电阻、电感和电容的电路里，各个元器件对电路中电流所起的阻碍作用叫做阻抗，其单位是欧姆，用符号Z表示，是一个复数，实部称为电阻，虚部为电抗。其中电容在电路中对交流电所起的阻碍作用称为容抗,电感在电路中对交流电所起的阻碍作用称为感抗，电容和电感在电路中对交流电引起的阻碍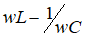
作用总称为电抗。我们常说的负载是电阻、电感的感抗、电容的容抗三种类型的复物，复合后统称“阻抗”。
如果
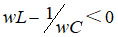
则称为容性负载。
如果
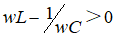
则称为感性负载。
根据阻抗表达式，在一个复平面上实部表示电阻，虚部表示电抗，则构成复阻抗平面，任意一个阻抗的计算结果，我们都可以放在这个复平面的对应位置。
如在 RLC 串联电路中，交流电源电压 U = 220 V，频率 f = 50 Hz，R = 30 Ω，L =445 mH，C =32 mF。
反射系数与S参数关系
在传输线系统中，信号沿传输线向前传播时，每时每刻都会感受到一个瞬态阻抗，这个阻抗可能是传输线本身的，也可能是中途或末端其他元件的。对于信号来说，它不会区分到底是什么，信号所感受到的只有阻抗。如果信号感受到的阻抗是恒定的，那么他就会正常向前传播，只要感受到的阻抗发生变化，不论是什么引起的（可能是中途遇到的电阻，电容，电感，过孔，PCB转角，接插件），信号都会发生反射。
当信号在链路阻抗不连续或端接阻抗不匹配的地方产生反射，反射信号幅度Vr 与入射信号幅度Vi 之比定义为反射系数（Reflection Coefficient） 
当源端与负载端阻抗已知是反射系数可以表示为
ZS、ZL分别为源端与负载端的阻抗，在有些地方可能会看到如下的定义
其中
是归一化负载值，即ZL / Z0。当中，ZL是负载端阻抗，Z0是传输线的特征阻抗（本征阻抗）值，通常会使用50Ω，该定义是理解史密斯圆图的基本公式。对于一个二端口网络有输入端反射系数
，与S参数之间关系如下
均为复数并可在史密斯圆图中表示出来。
假设PCB线条的特性阻抗为50欧姆，传输过程中遇到一个100欧姆的贴片电阻，暂时不考虑寄生电容电感的影响，把电阻看成理想的纯电阻，那么反射系数为：
信号有1/3被反射回源端。如果传输信号的电压是3.3V电压，反射电压就是1.1V。纯电阻性负载的反射是研究反射现象的基础，阻性负载的变化无非是以下四种情况：阻抗增加有限值、减小有限值、开路（阻抗变为无穷大）、短路（阻抗突然变为0）。
看下面case：初始电压是源电压Vs（2V）经过Zs（25欧姆）和传输线阻抗（50欧姆）分压，Vinitial=1.33V。
后续的反射率按照反射系数公式进行计算
源端的反射率，是根据源端阻抗（25欧姆）和传输线阻抗（50欧姆）根据反射系数公式计算为-0.33；
终端的反射率，是根据终端阻抗（无穷大）和传输线阻抗（50欧姆）根据反射系数公式计算为1；
我们按照每次反射的幅度和延时，在最初的脉冲波形上进行叠加就得到了这个波形，这也就是为什么，阻抗不匹配造成信号完整性不好的原因。
假设Z0一定，为50欧姆（为什么射频电缆特征阻抗定为50欧姆？这里面是有道道，主要是考虑到减少信号衰减和尽量提高发射功率两个因素做的折中并考虑到制作难度而定为了50欧姆，详细说明请自行百度）根据反射公式将得到以下结论：
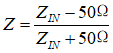
每一个Zin对应唯一的 “Γ”反射系数，定义归一化的负载阻抗：
此时反射系数的公式可重写为：
因此可将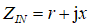
绘制在复阻抗平面上（从这里开始忘记Zin，只记得z（小写）和反射系数“Γ”）
将三根轴掰弯如下：
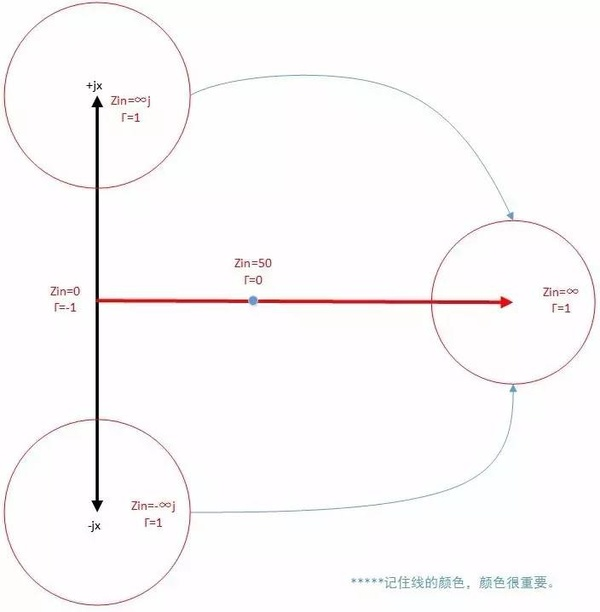
在复平面中，有三个点，反射系数都为1，就是横坐标的无穷大，纵坐标的正负无穷大。历史上的某天，史密斯老先生，如有神助，把黑色线掰弯了，把上图中，三个红色圈标注的点，捏到一起。
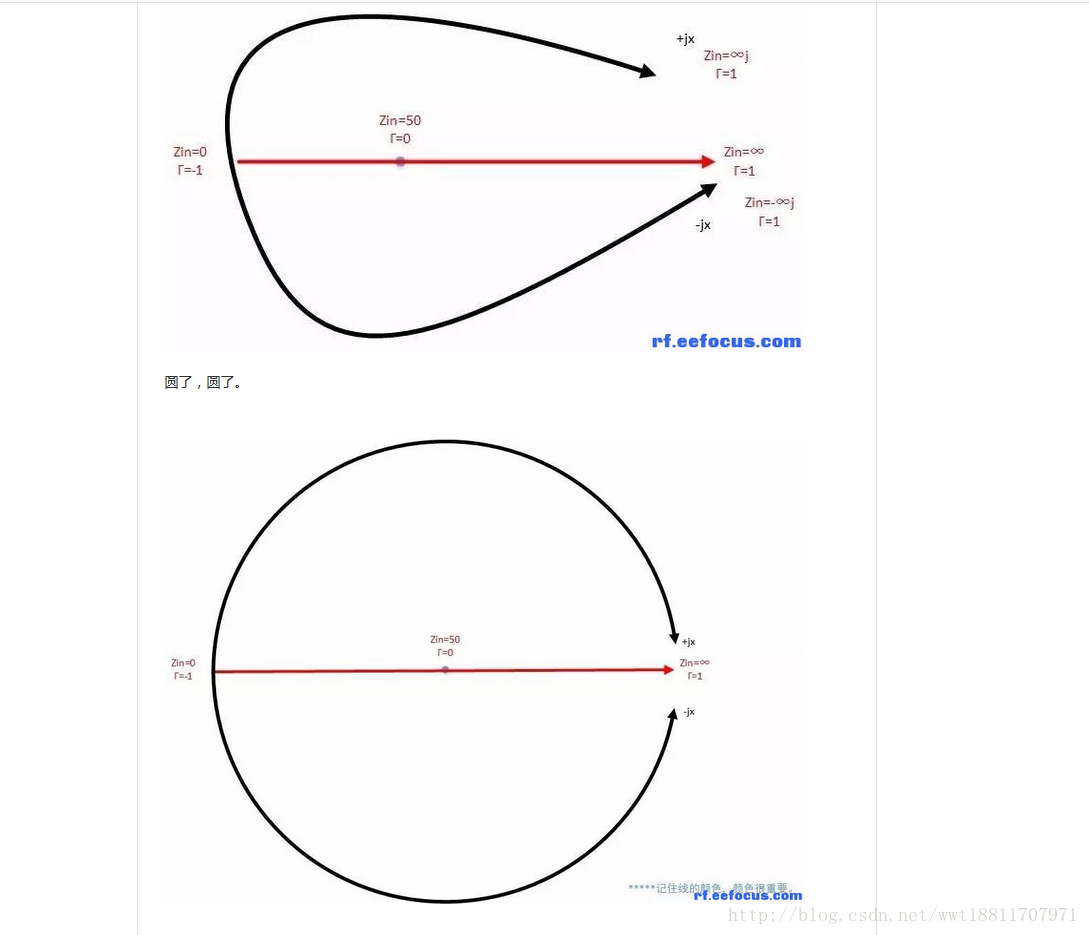
然后就行成了一个完美的圆：
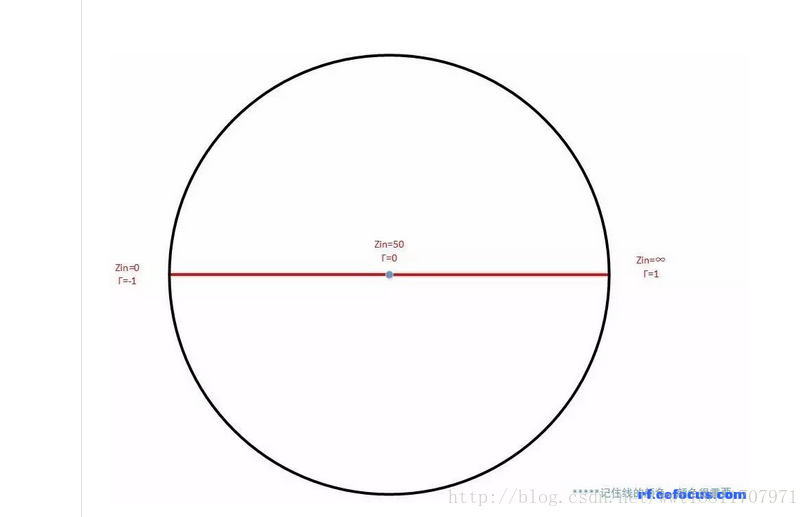
虽然，无穷大的平面变成了一个圆，但是，红线还是红线，黑线还是黑线。
同时我们在，原来的复平面中增加三根线，它们也随着平面闭合而弯曲。
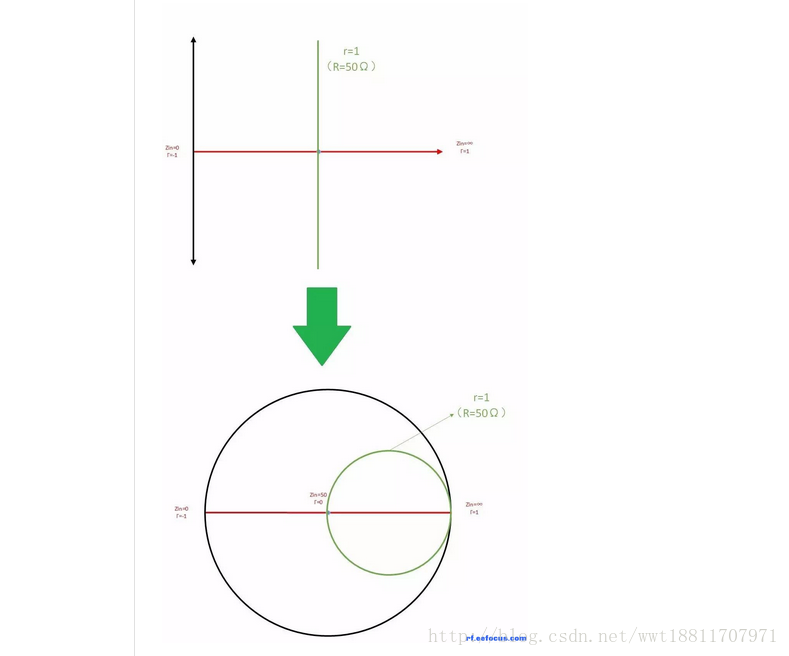
黑色的线上的阻抗，有个特点：实部为0；（电阻为0）
红色的线上的阻抗，有个特点：虚部为0；（电感、电容为0）
绿色的线上的阻抗，有个特点：实部为1；（电阻为50欧姆）
紫色的线上的阻抗，有个特点：虚部为-1；
蓝色的线上的阻抗，有个特点：虚部为1；
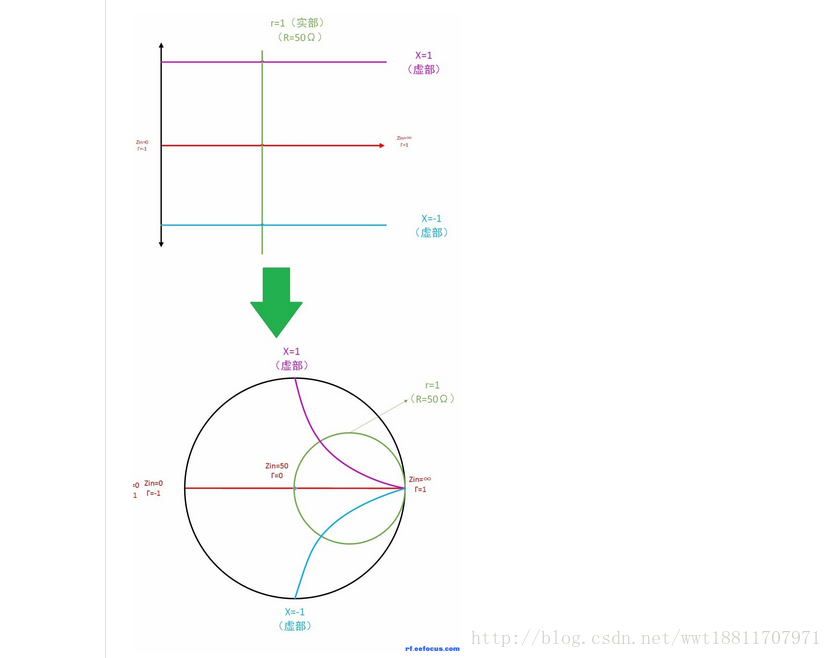
线上的阻抗特性，我们是从复平面，平移到史密斯原图的，所以特性跟着颜色走，特性不变。
下半圆与上班圆是一样的划分。
因为史密斯圆图是一种基于图形的解法，所得结果的精确度直接依赖于图形的精度。对于任意一个阻抗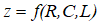
按照前面提到的阻抗计算公式计算并写成
的形式便可以在史密斯圆图中标记出来了。如下图所示为一款史密斯圆图软件，大家直接百度便可以找到，可以下载下来玩玩体会一下。
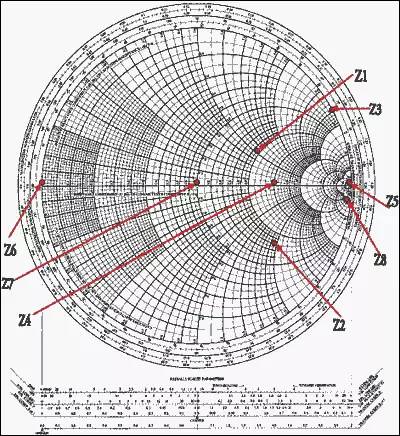
例：已知特性阻抗为50Ω，负载阻抗如下：
| Z1= 100 + j50Ω | Z2= 75 - j100Ω | Z3= j200Ω | Z4= 150Ω |
| Z5= ∞ (an open circuit) | Z6= 0 (a short circuit) | Z7= 50Ω | Z8= 184 - j900Ω |
对上面的值进行归一化并标示在圆图中(见图5)：
| z1= 2 + j | z2= 1.5 - j2 | z3= j4 | z4= 3 |
| z5= 8 | z6= 0 | z7= 1 | z8= 3.68 - j18 |
如果是“串联”，我们可以在清晰的史密斯原图上，先确定实部（红线上查找，原来复平面的横坐标），再根据虚部的正负，顺着圆弧滑动，找到我们对应的阻抗。（先忽略下图中的绿色线）
现在可以通过圆图直接解出反射系数Γ。
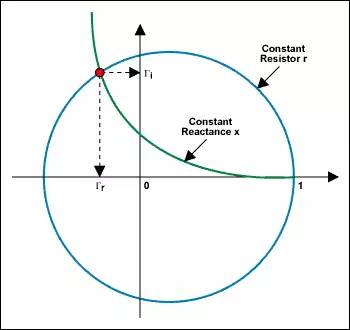
我们既可以通过直角坐标，去直接读取反射系数的值，也可以通过极坐标，读取反射系数的值。
直角坐标
画出阻抗点(等阻抗圆和等电抗圆的交点)，只要读出它们在直角坐标水平轴和垂直轴上的投影，就得到了反射系数的实部Γr和虚部Γi (见图6)。
该范例中可能存在八种情况，在图6所示史密斯圆图上可以直接得到对应的反射系数Γ：
| Γ1= 0.4 + 0.2j | Γ2= 0.51 - 0.4j | Γ3= 0.875 + 0.48j | Γ4= 0.5 |
| Γ5= 1 | Γ6= -1 | Γ7= 0 | Γ8= 0.96 - 0.1j |
从X-Y轴直接读出反射系数Γ的实部和虚部
极坐标
极坐标表示，有什么用？非常有用，这其实也是史密斯原图的目的。
2.4 红色阵营VS绿色阵营
刚刚我们已经注意到，史密斯原图，除了有红色的曲线，是从阻抗复平面掰弯，过来的红色世界。同时，在图中，还有绿色的曲线，他们是从导纳复平面，掰弯产生的。过程跟刚刚的过程是一样的。
那么这个导纳的绿色，有什么用呢？
并联电路，用导纳计算，我们会很便利。同时在史密斯原图中，我们用导纳的绿色曲线进行查询，也会很方便。
如图，这样并联一个电容，通过绿色的曲线很快就可以查询到对应的归一化阻抗和反射系数。
3、干什么？
解释和介绍了史密斯圆图这么长的段落，别忘了，我们想干什么。我们实际是希望，我们设计的电路反射系数越接近0越好。
但是，什么样的电路是合格的电路呢？反射系数不可能理想的为0，那么我们对反射系数，有什么样的要求呢？
我们希望反射系数的绝对值小于1/3，即反射系数落入史密斯圆图的蓝色区域中（如下图）。
这个蓝色的球，有什么特色呢？其实我们通过史密斯原图的数值已经清楚的发现。在中轴线，也就是之前说的红线上，分别是25欧姆，和100欧姆两个位置。即：Zin在1/2 Zo和2倍Zo之间的区域。
也就是，我们打靶打在蓝色区域，即认为反射系数是可以接受的。
本文内容为网上搜集整理而来，并非原创。主要内容来源于一篇史密斯(smith)圆图详解的文章
