通过TensorFlow训练神经网络模型

神经网络模型的训练过程其实质上就是神经网络参数的设置过程

在神经网络优化算法中最常用的方法是反向传播算法，下图是反向传播算法流程图：

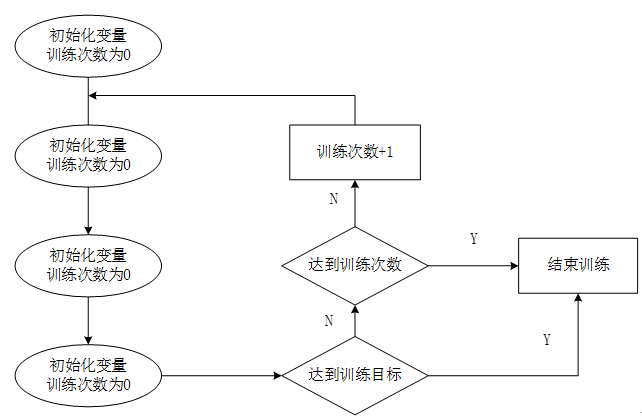
从上图可知，反向传播算法实现了一个迭代的过程，在每次迭代的开始，先需要选取一小部分训练数据，这一小部分数据叫做一个batch。然后这一个batch会通过前向传播算法得到神经网络的预测结果。计算出当前神经网络的预测答案与正确答案之间的差距（有监督学习，在训练时有一个标注好的数据集），最后根据预测值和真实值之间的差距，反向传播算法会相应的更新神经网络参数的取值，使在这个batch上神经网络模型的预测结果更接近真实答案。

 

通过TensorFlow实现反向传播算法的第一步是使用TensorFlow表达一个batch数据，但如果每轮迭代中选取的数据都通过常量来表示，会导致TensorFlow的计算图非常大。因为每生成一个常量，TensorFlow都会在计算图中增加一个节点。一般来书一个神经网络的训练过程会经过几百万轮甚至上亿轮的迭代，这样就导致计算图非常大，而且利用率低。为了避免这个问题，TensorFlow提供placeholder机制用于提供输入数据。placeholder相当于定义了一个位置，这个位置中的数据在程序运行时再指定，这样在程序中就不需要生成大量常量来提供输入数据，而只需要将数据通过placeholder传入TensorFlow计算图。在placeholder定义时，需要指定数据类型。下面程序是通过placeholder实现前向传播算法。

import tensorflow as tf


w1 = tf.Variable(tf.random_normal([2, 3], stddev=1, seed=1))
w2 = tf.Variable(tf.random_normal([3, 1], stddev=1, seed=1))

# 定义placeholder作为存放数据的地方。这里的维度不一定要定义，
# 但如果维度是确定的，给出维度会降低出错的概率
x = tf.placeholder(tf.float32, shape=(1, 2), name="input")

# 通过前项传播算法得到神经网络的输出
a = tf.matmul(x, w1)
y = tf.matmul(a, w2)
# 定义会话
sess = tf.Session()
# 定义初始化变量
init_op = tf.global_variables_initializer()
sess.run(init_op)
sess.run(w2.initializer)
# feed_dict是一个字典，在这个字典中需要给出每个使用placeholder定义变量的取值
print(sess.run(y, feed_dict={x: [[0.7, 0.9]]}))
sess.close()

在上面的程序中输入的是1x2矩阵（shape=（1, 2）），若改为n x 2的矩阵，就可以得到n个前向传播结果

在得到一个batch的前向传播结果后需要定义一个损失函数来刻画当前的预测值和真实答案之间的差距。然后通过反向传播算法来缩小预测值和真实值之间的差距。下面代码定义了一个损失函数，及反向传播算法

# 使用sigmoid函数将y转化为0-1之间的数值，转化后y代表预测正样本的概率，
# 1-y代表预测负样本的概率
y = tf.sigmoid(y)
# 定义损失函数，刻画预测值与真实值之间的差距
cross_entropy = -tf.reduce_mean(y_ * tf.log(tf.clip_by_value(y, le-10, 1.0)) +
                                (1 - y_) * tf.log(tf.clip_by_value(1-y, le-10, 1.0)))
# 定义学习率
LR = 0.001
# 定义反向传播算法优化神经网络参数
train_step = tf.train.AdamOptimizer(LR).minimize(cross_entropy)