索引结构
概述
许多查询只涉及表中的少量记录。例如"查找学号为'U2021001'的学生的专业",这个查询最多只涉及学生表中的一条记录。如果系统为了找到学号为"U2021001"的记录而读取整个学生表,这样的操作方式显然是低效的。理想情况下,系统应该能够直接定位到这条记录。为了支持这种访问方式,需要额外设计一些与表相关联的附加结构,我们称之为索引。
索引是这样的数据结构:它以一个或多个属性的值为输入,并能快速地定位具有该值的记录的位置。建立索引的属性(组)称为查找键(search key)。与表一样,索引结构同样存储在数据库文件中。例如,我们可以用一个数据文件来存储一个表,用一个索引文件来存储一个索引。一个数据文件可能拥有一个或多个索引文件。
由于索引是表的附加结构,当表的内容发生变化时,DBMS必须同步更新该表的索引,以确保索引的内容与表的内容一致。由此可见,索引虽然有助于提高查询性能,但是索引本身也会带来存储和维护开销,因此在一个数据库应用中,具体创建什么索引、以及创建多少索引,用户是需要权衡的。不过在查询的执行过程中,是否需要使用索引、以及使用哪些索引,则是由DBMS来决定的,用户并不能干涉。如何恰当地利用索引来提高查询的执行效率,是DBMS的重要工作。
数据库系统中存在不同类型的索引结构,这些索引结构之间没有绝对的优劣之分,只能说某种索引结构在某种特定的场景下是最合适的。评价一种索引结构一般参考以下指标:
- 查找类型:该索引结构能有效支持的查找类型,比如等值查找(Hash)、范围查找(B树)等。
- 查找时间:使用该索引结构找到一个特定索引项(集)所需的时间。
- 插入时间:插入一个新的索引项所需的时间,包括找到插入这个新索引项的正确位置,以及更新索引结构所需的时间。
- 删除时间:删除一个索引项所需的时间,包括找到待删除项所需的时间, 以及更新索引结构所需的时间。
- 空间开销:索引结构所占用的存储空间。
B树
B+树是一种平衡排序树,树中根结点到叶结点的每条路径的长度相同,并且保持键的有序排列。在B+树中进行搜索、顺序访问、插入和删除的时间复杂度均为O(log(n)),它是在数据插入和删除的情况下仍能保持其执行效率的几种使用最广泛的索引结构之一,几乎所有现代DBMS都使用B+树。
B+树可以定义为具有以下性质的m路搜索树:
- 除非整棵树只有一个结点,否则根结点至少有两个子结点;
- 除根结点外的所有内结点至少是半满的,即有⌈m/2⌉到m个子结点;
- 所有叶结点的深度相等;
- 叶结点中键的数量必须大于等于 ⌈(m-1)/2⌉ 且小于等于 m-1 ;
- 每个有k个键的内结点都有k+1个非空子结点;
- 叶结点中包含所有查找键值
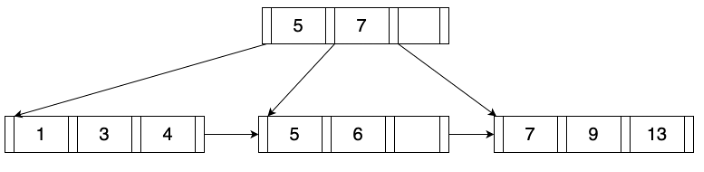
B+树的示意图如图3-1所示。树中的每个结点中都包含一个键/值对数组,这个数组是按键排序的。键/值对中的键来自索引的查找键,值则根据结点类型而有不同含义。如果结点是内结点,则值是指向子结点的指针。如果结点是叶结点,则结点中的值可能是记录ID,比如对于数据库中的非聚集索引,B+树中存放的就是指向记录位置的指针;叶结点中的值也可能是记录数据,比如对于聚集索引, B+树中存放的就是记录的实际数据。
在树的最底层,叶结点间通过兄弟指针链接起来,形成一个按所有键值大小排序的链表,以便更高效地支持范围查找等顺序处理。
图3-1中的B+树,其m的取值为4。在具体实现中,将B+树索引存储到磁盘文件中时,通常用一个页面来存储一个结点,在页面能够容纳的前提下,应该把m的值取得尽可能大,从而使得树的高度尽可能小。
散列表
散列表也叫哈希表,是一种常见的数据结构,它通过把键值映射到桶数组中的某个位置来加快查找记录的速度。散列表中包含两个关键元素:
- 散列函数 :散列函数h以查找键(散列键)为参数并计算出一个介于0到B-1之间的整数。
- 桶数组 :桶数组是一个编号从0到B-1、长度为B的数组,其中包含B个链表头,每个链表头对应一个桶,用于存储记录。
构造散列表时,如果一条记录的查找键为K,则将该记录链接到桶号为h(K)的桶中存储。
散列表在DBMS中被广泛运用,例如基于散列表来组织数据文件、基于散列表来构造索引文件、或者基于散列表进行连接运算(??)等。当散列表的规模大到内存难以容纳时,或者出于数据持久化的目的,就需要将散列表存储在磁盘中。本教程主要讨论散列表在磁盘上的实现。
磁盘中的散列表与内存中的散列表存在一些区别。首先,桶数组是由页面组成,而不是由指向链表的指针组成;其次,散列到某个桶中的记录是存储在磁盘上的页面而非内存中。因此,磁盘上的散列表在设计时需要考虑访问磁盘的I/O代价以及表规模的扩展问题。
可扩展散列表
与静态散列表相比,可扩展散列表在结构上做了以下改变:
- 增加了一个间接层,用一个指向页面的指针数组(桶地址表)而非页面数组来表示桶数组。
- 指针数组能动态增长,且数组长度总是2的幂,因此数组每增长一次,桶的数量就翻倍。
- 并非每个桶都单独拥有一个页面。如果多个桶的记录只需一个页面就能放下,那么这些桶可能共享一个页面,即多个桶指针指向同一个页面。
- 散列函数h为每个键计算出一个长度为N的二进制序列,N的值足够大(比如32),但是在某一时刻,这个序列中只有前i位(i≤N)被使用,此时桶的数量为 2i个。
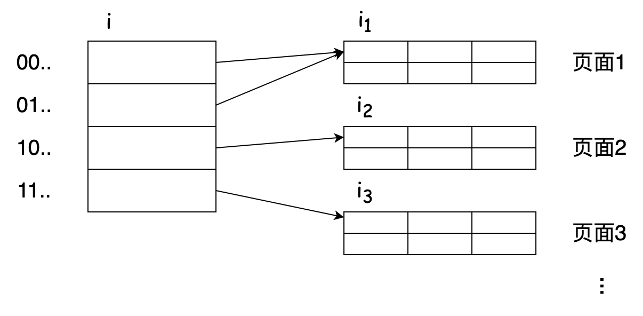
向可扩展散列表中插入键值为K的记录的方法如下:
计算h(K),取出该二进制序列的前i位,并找到桶数组中编号与之相等的项,定位到该项对应的页面,假设该页面的编号为j;
如果页面j中还有剩余空间,则将该记录插入该页面,操作结束;
如果页面j已满,则需要分裂该页面:
a) 如果\(i=i_{j}\),说明在桶地址表中只有一个表项指向页面j,此时分裂该页,需要增加桶地址表的 大小,以容纳由于分裂而产生的两个桶指针。令i=i+1,使桶地址表的大小翻倍。桶地址表扩 展后,原表中的每个表项都被两个表项替代,且这两个表项都包含和原始表项一样的指针, 所以也应该有两个表项指向页面j。此时,分配一个新的页面n,并让第二个表项指向页面n。 将ij和in的值均置为当前的i值,并将原页面j中的各条记录重新散列,根据前i位来确定该记录 是放在页面j中还是页面n中,然后再次尝试插入新记录。极端情况下,新纪录要插入的页面 可能仍然是满的,说明原页面j中的所有记录在分裂后仍然被散列到了同一个页面中,此时需 要继续上述分裂过程,直至为新纪录找到可存放的空间。
b) 如果\(i> i_{j}\),说明在桶地址表中有多个表项指向页面j,此时不需要扩大桶地址表就能分裂页面 j。分配一个新的页面n,将ij和in置为原ij加1后的值;调整桶地址表中原来指向页面j的表项, 其中一半仍指向页面j,另一半则指向新创建的页面n;重新散列页面j中的各条记录,将其分 配到页面j或页面n中,并再次尝试插入新记录。与上一种情况一样,插入仍有可能失败,此 时需继续进行页面分裂的处理。
以下是一个可扩展散列表的例子。图3-6(a)所示为一个小型的可扩展散列表,假设其散列函数h能产生4位二进制序列,即N=4。散列表只使用了1位,即i=1。此时桶数组只有2项,一个编号为0,一个编号为1,分别指向两个页面。第一页存放所有散列值以0开头的记录,第二页存放所有散列值以1开头的记录。每个页面上都标注了一个数字,表示由散列函数得到的二进制序列中的前几位用于判定记录在该页面中的成员资格。目前两个页面都只用了1位。
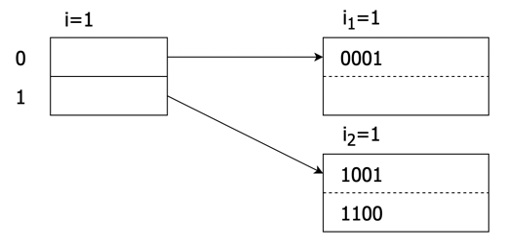
接下来向表中插人一个散列值为1010序列的记录。因为第一位是1,所以该记录应放入第二个页面,但第二页已经满了,因此需要分裂该页。而此时i2=i=l,因此先要将桶数组翻倍,令i=2,将数组的长度扩展为4。
扩展桶数组后,以0开头的两个项都指向存放散列值以0开头的记录的第一页,且该页上标注数字仍然为1, 说明该页中记录的成员资格只由其散列值的第一位判定。而原本存放散列值以1开头的记录的页面则需要分裂,把这个页面中以10开头和11开头的记录分别存放到两个页面中。在这两个页面上方标注的数字是2,表示该页面中记录的成员资格需要使用散列值的前两位来判定。改变后的散列表如图3-6(b)所示。
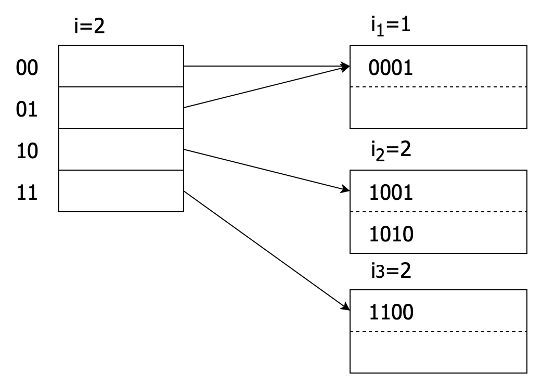
可扩展散列表的优点在于每个桶只有一个页面,所以如果桶地址表小到可以驻留在内存的话,查找一个记录最多只需要一次磁盘I/O。但是由于它是以桶数组翻倍的形式扩展的,所以也存在以下缺点:
- 随着i的增大,每次桶数组翻倍时需要做的工作将越来越多(分裂时,一分为2,需要的位i+1),而且这些工作还会阻塞对散列表的并发访问,影响插入和并发操作的效率。
- 随着i的增大,桶地址表会越来越大,可能无法全部驻留在内存,或者会挤占其他数据在内存中的空间,导致系统中的磁盘I/O操作增多。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号