单源最路径算法总结

1．相关概念

         带权有向图上顶点u→v间的最短路的权为：

                  

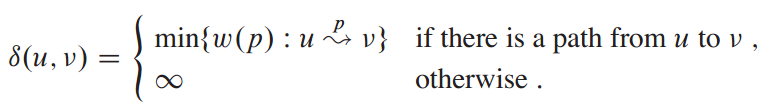
         负权值边、负权回路及正权回路

         最短路径的表示：最短路径树

         类似于广度优先搜索得出的广度优先树，增加一个前驱数组π[V]，可以依次求出源点到各点的最短路径；在算法结束时，如下的G_π就是最短路径树。

         由π值可以推导出前驱子图G_π=(V_π,E_π)，其顶点集V_π为G中所有具有非空前驱的顶点集合，再添加上源点s：V_π={v∈V:π[v]≠NIL}∪{s}，有向边集E_π={(π[v],v):v∈V_π-{s}}.

         松弛技术

         增加一个数据结构d[V]：描述s→v的最短路径上权值的上界。

         最短路径估计和前驱初始化函数（复杂度为Θ(V)）

INITIALIZE-SINGLE-SOURCE(G,s)
    for each vertex v∈G.V
        d[v] = ∞
        π[v] = NIL
    d[s] = 0

         对一条权值为w的边(u,v)的松弛过程如下：

RELAX(u,v,w)
    if d[v]>d[u]+w(u,v)
        d[v] = d[u]+w(u,v)
        π[v] = u

2．求单源最短路径的Bellman-Ford算法

　　原理：

　　运用松弛技术，对每个顶点v，逐步减少从源s→v的最短路权的估计值d[v]直到其达到实际最短路径的权δ(s,v)为止。 

ELLMAN-FORD(G,w,s)
    INITIALIZE-SINGLE-SOURCE(G,s)
    
    for i= 1 to |G.V|-1
        for each edge (u,v)∈G.E
            RELAX(u,v,w)
    
    //判断是否包含源点可达的负权回路        
    for each edge (u,v)∈G.E
        if d[v]>d[u]+u(v,w)
            return false;
    return true

　　说明：

　  1)实现的关键，每一趟RELAX都必须按照任一固定的顺序进行（实际并不需要，这样只是利于显示），每一次循环都松弛了所有的|G.E|条边，这相当于s=v₀→v=v_k（v为任一点）的最短路径p=<v₀,v₁,…,v_k>可以依次被松弛，即第i次循环包含对边(v_i-1,v_i)的松弛，这样可确定d[v]=d[v_k]=δ[s, v_k]=δ[s, v]；

    2)本算法可以处理有负边、负回路的情况；

    3)算法的时间复杂对为O(VE).

3．有向无回路（dag）图中的单源最短路径

         原理：BELLMAN-FORD算法因为没有按照路径顺序所以每次循环都是对松弛所有的|E|条边，如果对顶点进行拓扑排序，则对顶点可按照拓扑顺序进行松弛，如果u到v存在一条路径，则在拓扑序列中u先于v。在拓扑排序的过程中我们仅对顶点执行了一趟操作。当对每个顶点处理时，松弛从该顶点出发的所有边。这相当于减少了松弛的边数，每条边总共被松弛一次；

         算法：

DAG-SHORTEST-PATHS(G,w,s)
    topologically sort the vertices of G
    INITIALIZE-SINGLE-SOURCE(G,s)
    for each vertex u, taken in topologically sorted order
        for each vertex v∈G.Adj[u]
            RELAX(u,v,w)

      说明：

　　1)算法的时间复杂度为Θ(V+E)，此时图是用邻接表表示的;

　　2)算法可以处理存在负权边的情况；

     3)算法有一个重要应用时确定dag图的关键路径。关键路径是通过dag的一条最长路径，它对应于一个有序的工作序列的最长时间；有两种方法：对边的权去负值，运行一遍本过程；初始化过程∞换为-∞，RELAX中>换成<号；

4．Dijkstra算法

　　原理：

　　贪心法,类似于最小生成树算法。设置了一顶点集合S，从源点s到集合S中的顶点的最终最短路径的权值均已确定。算法反复选择具有最短路径估计d[u]的顶点u∈V-S，并将u加入到S中。

　　算法：

　　用到的数据结构：按关键之d排序的最小优先队列Q

IJKSTRA(G,w,s)

//初始化
    INITIALIZE-SINGLE-SOURCE(G,s)
    S = ∅
    Q = G.V
    
    while Q≠∅
        u = EXTRACT-MIN(Q)
        S = S∪{u}
        for each vertex v∈G.Adj[u]
            RELAX(u,v,w)

　　说明：

　　1)本算法只能用于无负权边、无负回路的情况；无负回路的要求是显然的，对于无负权边，这是因为本算法是以最短路径估计的贪心法，所以当前选择加入S的顶点u只能确定是此时u的最短路径估计，如果没有负权边的话，则可以保证该值就是此时的最短路径权值，否则的话，则之后如果有一复权值边则可能使的该点的最短路径估计值变小；

　　2)算法终止时，前驱子图G_π是以s为根的最短路径树；

　　3)类似于Prim算法，算法的时间复杂度依赖于图的存储结构和优先队列的具体实现：

Minimum edge weight data structure	Time complexity (total)
Searching, adjacency matrix	O(V2+V)= O(V2)
binary heap, adjacency list	O((V+E)logV) = O(ElogV)
Fibonacci heap, adjacency list	O(E+VlogV)

　　4)同广度优先搜索算法、prim算法有异同

     与广度优先算法的相似之处在于：前者的集合S相当于后者的褐色顶点集合，正如集合S中的顶点有着最终的最短路径权值，后者的黑色顶点集合也有着正确的广度优先距离；

     与Prime算法的相似之处在于：两种算法均采用最小优先队列来找出给定集合以外“最轻”的顶点，然后把该顶点加入到集合中，并相应地调整该集合以外剩余顶点的权；

     与Prim算法的不同之处在于：Dijkstra算法每次加入S的为具有最短路径估计的顶点，而Prim算法加入集合A的为具有与A相连最小权值边的顶点；另外，前者在添加顶点u之后，进行的是对u邻接点的RELAX操作，而后者进行的是确定最小权值边的操作。

 

参考文献：《算法导论》