算法题一些小总结(java相关)

虽然题没做几道，但是感觉还是有一些规律性的内容可以总结出来。比如一些常用的处理技巧

1.map排序

　　TreeMap是可以自动按照key排序的（升序），但是如果遇到需要按照value排序的情况，那么就不能使用TreeMap，因为会强行按照key排序。所以需要使用HashMap存储数据，然后把Map的EntrySet转换成list，然后使用Collections.sort排序, 根据排序需求改写comparator。

　　如需要按照value从大到小来排序：

//map排序，按照value排序
List<Map.Entry<Integer, Integer>> list = new ArrayList<Map.Entry<Integer,Integer>>(map.entrySet());
Collections.sort(list, new Comparator<Map.Entry<Integer, Integer>>() {
    @Override
    public int compare(Entry<Integer, Integer> o1, Entry<Integer, Integer> o2) {
        // TODO Auto-generated method stub
        return o2.getValue().compareTo(o1.getValue());
    }
});

map.entrySet()：把HashMap类型的数据转换为集合类型，获取键值对的集合

2.返回前k个频率最大的元素（返回k个最大的元素）

　　借助堆来实现，对于k频率之后的元素就不再处理了。

　　首先构建一个最小堆，然后遍历hashmap，来维护一个元素数目为k的最小堆。每次都将新的元素与堆顶元素进行比较，如果新元素的频率比堆顶元素大，则弹出堆顶元素，将新元素添加进堆里。最终堆里的k个元素就是k个高频元素。

　　为什么求最大k个元素，是构建最小堆？因为这样堆顶元素是 当前k个元素里最小的，那么新来的只要大于k个元素里最小的，那么替换掉它就好了。

//构建最小堆
PriorityQueue<Integer> pqIntegers = new PriorityQueue<>(new Comparator<Integer>() {

    @Override
    public int compare(Integer o1, Integer o2) {
        // TODO Auto-generated method stub
        return map.get(o1)-map.get(o2);
        }
});
//遍历map，用最小堆保存频率最大的k个元素
for(Integer key: map.keySet()) {
    //如果现在最小堆中不够k个元素，那么直接加就好了
    if (pqIntegers.size()<k) {
        pqIntegers.add(key);
    }
    //如果新元素的频率 大于 堆顶元素，那么弹出堆顶元素，把新元素加进堆里
    else if (map.get(key)>map.get(pqIntegers.peek())) {
        pqIntegers.remove();
        pqIntegers.add(key);
    }
}
//取出最小堆中的元素
List<Integer> ret = new ArrayList<>();
while(!pqIntegers.isEmpty()){
　　ret.add(pqIntegers.remove());
}

 3.链表题，如求两个链表的公共部分。在笔试的时候可以直接当作数组来处理，因为链表非常容易超时。

 4.回溯法解 排列、组合、子集问题

给出一个回溯算法的模板

private void dfs(所有路径的集合, 当前路径, 选择列表){
      if(满足结束条件){
            所有路径的集合.add(当前路径);
            return;
      }  
      if(满足剪枝的条件){
            return;
      }
      //如果是排列的话，顺序相关，所以选择nums[i]可以从0-选择列表.length；而组合和子集需要一个index记录当前遍历到哪个选择，为了排除选择过的数，选择应该从index-选择列表.length
      for(选择nums[i] in 选择列表){
             剪枝（可选）
             做选择(将当前选择加到当前路径)
             //如果元素可重复被选择，那么可以从i开始。如果不可重复被选择，就要从i+1
             dfs(所有路径的集合, 当前路径, 选择列表)  
             撤销选择
      }
}

三个类型的问题的问法如下：

子集：输入一个不包含重复数字的数组，要求算法输出这些数字的所有子集。（包括空集和本身）
组合：输入两个数字 n, k，算法输出 [1..n] 中 k 个数字的所有组合。（指定长度，顺序无关，但是不能重复。即[1,2]和[2,1]算重复）
排列：输入一个不包含重复数字的数组 nums，返回这些数字的全部排列。（长度就是数组的长度，顺序相关，不能有重复。即[1,2,3]和[1,3,2]不算重复）

每个类型的套用模板的解法：

//组合，candidates中的数字可以被无限次重复被选取
class Solution {
    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        List<List<Integer>> ret = new ArrayList<>();
        Arrays.sort(candidates);
        dfs(candidates, target, ret, 0, new ArrayList<Integer>());
        return ret;
    }

    private void dfs(int[] candidates, int target, List<List<Integer>> ret, int index, ArrayList<Integer> temp){
        //什么时候剪枝：目标数<0
        if(target<0){
            return;
        }
        //什么时候满足条件：目标数=0
        if(target==0){
            ret.add(new ArrayList<>(temp));
            return;
        }
        //当前路径可能是可行路径，逐步选择当前节点下所有可能的路径
        //i依然从index开始，因为求的是组合。可以加上这个值，但是不能加比这个值更小的值，那样就重复了
        for(int i=index; i<candidates.length; i++){
            //保存当前数据
            temp.add(candidates[i]);
            //递归，记住已经走过这个节点，继续向下走一步
            //为什么还是i，而不是i+1？因为可重复，所以第一个数取candidates[i]，第二个数还可以取candidates[i]
            dfs(candidates, target-candidates[i], ret, i, temp);
            //回溯清理，该节点下所有路径都走完了，清除堆栈
            temp.remove(temp.size()-1);
        }
    }
}

 

//子集,给定一组不含重复元素的整数数组 nums，返回该数组所有可能的子集（幂集）。
class Solution {
    public List<List<Integer>> subsets(int[] nums) {
        List<List<Integer>> ret = new ArrayList<>();
        Arrays.sort(nums);
        dfs(ret, nums, 0, new ArrayList<Integer>());
        return ret;
    }

    private void dfs(List<List<Integer>> ret, int[] nums, int index,  ArrayList<Integer> temp){
        if(index>nums.length){
            return;
        }
        ret.add(new ArrayList<>(temp));
        //添加一个index记录当前加入到子集中元素的位置，排除已经选择过的数字
        for(int i=index; i<nums.length; i++){
            temp.add(nums[i]);
            dfs(ret, nums, i+1, temp);
            temp.remove(temp.size()-1);
        }
    }
}

//排列 给定一个 没有重复 数字的序列，返回其所有可能的全排列。
class Solution {
    public List<List<Integer>> permute(int[] nums) {
        List<List<Integer>> ret = new ArrayList<>();
        Arrays.sort(nums);
        dfs(ret, nums, new ArrayList<>());
        return ret;
    }

    private void dfs(List<List<Integer>> ret, int[] nums, ArrayList<Integer> temp){
        if(temp.size() == nums.length){
            ret.add(new ArrayList<Integer>(temp));
            return;
        }
        for(int i=0; i<nums.length; i++){
            //使用contains方法排除已经选择的数字
            if(temp.contains(nums[i])){
                continue;
            }
            temp.add(nums[i]);
            dfs(ret, nums, temp);
            temp.remove(temp.size()-1);
        }
    }
}

需要注意的技巧在于当每个数字在一个集合里只能使用一次时，就需要去重。去重的方法是

    private void dfs(List<List<Integer>> ret, int[] candidates, int target, int index, ArrayList<Integer> temp){
        //剪枝
        //满足条件
        //回溯
        for(int i=index; i<candidates.length; i++){
            //小剪枝
            if(i>index && candidates[i]==candidates[i-1]){
                continue;
            }
            //选择
            temp.add(candidates[i]);
            //回溯
            dfs(ret, candidates, target-candidates[i], i+1, temp);
            //撤销选择
            temp.remove(temp.size()-1);
        }
    }

关于这个去重，我觉得这个解答讲得比较清楚。比如[1,2,5]，我们把2出现的位置叫做第二层级，5出现的叫做第三层级，我们只允许第二层级和第三层级都出现2，即[1,2,2].但是不允许第二层级出现两次2，否则是会出现重复的，如[1,2,...]和[1,2,...]。也就是我们要让一个层级中，必须出现且只出现一个2，那么就要放过第一个出现的重复2(i=index)，但不放过第二个出现的重复2(i>index).

回溯法还有一个经典应用场景--N皇后问题

class Solution {
    List<List<String>> ret = new ArrayList<>();
    public List<List<String>> solveNQueens(int n) {
        //棋盘&初始化
        char[][] chess = new char[n][n];
        for(int i=0; i<n; i++){
            for(int j=0; j<n; j++){
                chess[i][j] = '.';
            }
        }
        back(chess, 0);
        return ret;
    }

    public void back(char[][] chess, int row){
        //搜索成功
        if(row == chess.length){
            ret.add(covertToString(chess));
            return;
        }
        //回溯放皇后
        for(int col=0; col<chess.length; col++){
            if(checkRight(chess, row, col)){
                chess[row][col] = 'Q';
                back(chess, row+1);
                chess[row][col] = '.';
            }
        }
    }
    //一行一行col往下放置，所以判断列row是否可以放置即可
    public boolean checkRight(char[][] chess, int row, int col){
        //判断当前列是否可以放置,即判断坐标上面有没有皇后
        for(int i=0; i<row; i++){
            if(chess[i][col]=='Q'){
                return false;
            }
        }
        //判断斜线是否能放置，左上角
        int i=row-1, j=col-1;
        while(i>=0 && j>=0){
            if(chess[i][j]=='Q'){
                return false;
            }
            i--;
            j--;
        }
        //判断反斜线是否能放置，右上角
        i=row-1;
        j=col+1;
        while(i>=0 && j<chess.length){
            if(chess[i][j]=='Q'){
                return false;
            }
            i--;
            j++;
        }
        return true;
    }

    public List<String> covertToString(char[][] chess){
        List<String> list = new ArrayList<>();
        for(int i=0; i<chess.length; i++){
            list.add(new String(chess[i]));
        }
        return list;
    }
}

解决迷宫系列问题：同样可以采用dfs/bfs来解决，但是这个关键在于 迷宫中的球不是一步一停，而是朝着某个方向一直滚，直到遇到墙/边缘才停。

 for(int[] dir: dirs) {
     int newX = curX;
     int newY = curY;
     //要滚到墙壁才会停止
     while(newX+dir[0]>=0 && newX+dir[0]<rows &&
             newY+dir[0]>=0 && newY+dir[1]<cols &&
             maze[newX+dir[0]][newY+dir[1]]!=1) {
                    newX+=dir[0];
                    newY+=dir[1];
      }
     //看是否是曾经访问过的位置
      if(visited[newX][newY]==false) {
             queue.add(new int[] {newX, newY});
             visited[newX][newY] = true;
      }
}

bfs解决这类问题的模板

private boolean bfs(int[][] maze, int[] start, int[] des, int rows, int cols) {
    //构建一个已访问的标记    
    boolean[][] visited = new boolean[rows][cols];
    //建一个队列用来存储可访问的位置，当访问完这个位置之后，把这个位置可访问的其他位置加进去。先把开始结点加进去
    Queue<int[]> queue = new LinkedList<>();
    queue.add(start);
    //将初始节点标记为已访问，选择初始节点开始
    visited[start[0]][start[1]] = true;
    while(!queue.isEmpty()) {
            //取出队列里的节点，当前坐标
            int[] cur = queue.poll();
            int curX = cur[0];
            int curY = cur[1];
            //如果找到终点
            if(curX==des[0] && curY==des[1]) {
                return true;
            }
            //否则上下左右不断遍历
            for(int[] dir: dirs) {
                int newX = curX+dir[0];
                int newY = curY+dir[1];
                //看是否是曾经访问过的位置，即判断该节点是否可访问。如果可访问，那么就把该节点入队
                if(visited[newX][newY]==false) {
                    queue.add(new int[] {newX, newY});
                    visited[newX][newY] = true;
                }
            }
        }
        return false;
    }        

5.贪心算法

对问题求解时，总是做出当前看来最好的选择。即不从整体最优上加以考虑，而是某种意义上的局部最优解。

典型例题：435无重叠区间

给定一个区间的集合，找到需要移除区间的最小数量，使剩余区间互不重叠。

应该先计算最多能组成的不重叠区间个数，用总的区间个数-不重叠区间个数=需要移除的个数。

那么最多，应该在每次选择的时候，选择区间的右端点应该尽量小，这样留给后面的可选择空间就越大，从而使得后面能选择的区间个数也就越大。

因此步骤应该是：按照区间的右端点（结尾）进行升序排序，每次都选择结尾最小的，并且与前一区间不重叠。

class Solution {
    public int eraseOverlapIntervals(int[][] intervals) {
        if(intervals==null){
            return 0;
        }
        //根据区间的右端点（结尾） 升序排列
        Arrays.sort(intervals, new Comparator<int[]>(){
            public int compare(int[] o1, int[] o2){
                if(o1[1] > o2[1]){
                    return 1;
                }
                if(o1[1] < o2[1]){
                    return -1;
                }
                else{
                    return 0;
                }
            }
        });
        //计算最多能组成的 不重叠区间 个数
        int count = 1;
        int end = intervals[0][1];//取第一个区间的结尾 作为当前区间结尾的最小值
        for(int i=0; i<intervals.length; i++){
            if(intervals[i][0] < end){//只要下一个区间的左端点 在上一个区间右端点的左边，就重叠
                continue;
            }//否则就是不重叠，把该区间加到 不重叠区间集合 中
            end = intervals[i][1];//更新所有区间的结尾
            count++;
        }
        return intervals.length-count;
    }
}

类似的452.用最少数量的箭引爆气球，跟这一题的思路比较类似。其实就是相当于求不重叠区间的个数。

6. 边界问题处理

以下判断条件表示，如果数组中有一个0，那需要它的左右两侧都是0。对于数组的第一个和最后一位，只需要考虑一侧是否为0。

整体的情况枚举如下：简称数组为a[]

a[i]=0 && a[i-1]=0 &&a[i+1]=0

a[i]=0 && i=0 && a[i+1]=0

a[i]=0 && i=length-1 && a[i-1]=0

因为如果i在数组第一位，那么i肯定不符合i=length-1，就去判断后面那个条件a[i+1]=1就好。即i=0不需要和a[i-1]=0一起判断，所以可以把他们归为并集，这两个只能同时符合一个条件，因为i=0时，i-1就不在数组的范围内了。

if(flowerbed[i]==0 && (i==0 || flowerbed[i-1]==0) && (i==flowerbed.length-1 || flowerbed[i+1]==1))

 7.滑动窗口法

解决 查找满足一定条件的连续区间（子串、子数组） 的问题。

整体思路如下:（即使用双指针）

1.初始化：left=right=0，把索引闭区间[left,right]称为 窗口
2.寻找可行解：不断增加right指针扩大窗口，知道窗口中的字串符合条件（比如包括指定字符串中的所有字符/窗口中的字串之和小于x）
3.优化可行解：此时停止增加right，转而增加left，缩小窗口[left, right]，直到窗口中的字符串不再符合要求，left不再继续移动。同时，每次增加left们都要更新一轮结果
4.左右指针轮流前进，窗口大小增增减减，窗口不断向右滑动：重复2&3步，即先移动right，再移动left，直到right到达字符串的尽头

例如，在数组a中，当连续数字的和大于s时会触发报警，求最长连续的没有触发报警的课程数量。

    private static int cal(int s, int[] a) {
        // TODO Auto-generated method stub
        //最大连续边界
        int max = 0;
        int left = 0; //窗口左边界
        int right = 0;//窗口右边界
        int cur = 0;//窗口故障总和
        
        while(right<a.length) {
            //如果没有报警，那么判断是否需要更新最大值，窗口向右扩展一格
            if(cur+a[right]<=s) {
                cur += a[right];
                right++;
            }
            //报警
            else {
                max = Math.max(max, right-left);
                /*//如果左右在同一个位置，即窗口大小为1，那么向右扩展一格
                if (left == right) {
                    right++;
                }*/
                //最左端位置向右移一格
                cur -= a[left];
                left++;
            }
        }
        return max;
    }

8. 最大组合数

给定一个数列，任意N个数可以组成一组被消掉，最多可以组成多少组。

如[0,2,3,99]，规定3个数成为一组，那么最多2组，因为第二三四组两组之后，剩下的变成了[0,0,1,97]，无法形成别的组。

思考方式：对数列进行排序，判断剩余可选的组是否还大于N，把最小的一个数和最多的N-1个数，数量-1。再排序，依次循环，直到剩余可选的组不足N，就不可以再分了。

链接：https://www.nowcoder.com/questionTerminal/180f62aa9b634cb4a6cfbdbb53c353bf
来源：牛客网

猿辅导课堂上老师提供了一些角色，学生可以从中选择一个自己喜欢的角色扮演，每3个不同的角色就可以组成一个小组，进行分组对话。    当老师点击开始分组对话按钮的时候，服务器会为已经选择自己角色的同学分配对话小组，请问最多能组成多少个对话小组？ 

解答：

    
//p表示每个角色的选择人数Pi
private static int maxTeam(int[] p) {
        // TODO Auto-generated method stub

        int max = 0;//最多可以组成的组数
        while(true) {
            Arrays.sort(p);
            int index;
            //找到当前第一个没有分配完的角色
            for(index=0; index<p.length; index++) {
                if (p[index]==0) {
                    continue;
                }
                else {
                    break;
                }
            }
            //如果剩余可选的角色不足3个，那么就退出循环
            if (index>p.length-3) {
                break;
            }
            //否则把最少的一个角色，和最多的两种角色数量-1
            else {
                p[index]--;
                p[p.length-1]--;
                p[p.length-2]--;
                max++;
            }
        }
        
        return max;
    }

9.有a升和b升的杯子，求最少多少次能得到c升水？

数学规律：a升和b升的杯子，可以倒出k*gcd(a,b)升水。

若gcd(a,b)=x，必然存在p和q，使得a*p+b*q=x。此时p和q必定一正一负，如果q为负，那么倒水的方式是：装满a水杯p次，再倒到b水杯q次，剩下的水量就是x。因此能量出c，当且仅当x能整除c。

如a=5，b=3，要量出4升水。5和3的最大公约数为1，因此5*(-1)+3*2=1。我们将b灌满，倒到a中；再将b灌满，倒到a中，这时b中剩下1升水。因为1升可以整除4升，即4个1升可以得到4升水。说明可装，那么最少次数当然是，如果此时a>c>b>x，并且x可以整除b，那么如果c>b*n，可以用b来直接代替若干次（n次）x的操作。

10.递归解决链表问题的步骤

1.首先写出终止条件
2.考虑返回什么值
3，

例：leetcode83，给定一个排序链表，删除所有重复节点，使得每个元素只出现一次。

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) { val = x; }
 * }
 */
class Solution {
    public ListNode deleteDuplicates(ListNode head) {
        //终止条件：当head为空，或者head只剩下一个节点，当然不可能重复
        if(head==null || head.next==null){
            //返回值:返回经过去重处理的链表头节点
            return head;
        }
        //递归：head的下一个节点指向一个去重的链表
        //判断当前head和head.next是否相等，如果相等就做去重，即忽视掉当前的head.next节点。不相等就计入当前的head.next节点
        if(head.val == head.next.val){
            head = deleteDuplicate(head.next);
        }

          else{

             head.next = deleteDuplicates(head.next);

          } 

return head;
    }
}

 附上这个题非递归的解法

class Solution {
    public ListNode deleteDuplicates(ListNode head) {
        if(head==null || head.next==null){
            return head;
        }
        List p = head, q = head.next;
        while(q!=null){
            //相同的就跳过
            if(p.val == q.val){
                q = q.next;
            }
            //不相同的就连接m，并且p,q同时后移
            else{
                p.next = q;
                p = q;
                q = q.next;
            }
        }
        //记得连接最后一个节点
        p.next = q;
        return head;
    }
}

变形：leetcode82，给定一个排序链表，删除所有含有重复数字的节点，只保留原始链表中 没有重复出现的数字。

class Solution {
    public ListNode deleteDuplicates(ListNode head) {
        if(head==null || head.next==null){
            return head;
        }
        if(head.val == head.next.val){
            //跳过所有相等的节点：如果head后面有值 && 与head的值相等，就找到不相等为止
            while(head.next!=null && head.val==head.next.val){
                head = head.next;
            }
            //从第一个不等于head值的元素开始处理
            head = deleteDuplicates(head.next);
            return head;
        }
        //不相等，直接连接，从head->next开始接着处理后面的链表
        else{
            head.next = deleteDuplicates(head.next);
            return head;
        }
        
    }
}

非递归版本

class Solution {
    public ListNode deleteDuplicates(ListNode head) {
        if(head==null || head.next==null){
            return head;
        }
        //由于如果开头就重复，需要把头节点去掉。所以增加一个哑节点，便于处理
        ListNode dummy = new ListNode(-1);
        dummy.next = head;

        ListNode pre = dummy;
        ListNode cur = head;

        while(cur!=null && cur.next!=null){
            //不直接比较pre和cur的val，因为初始的时候pre指向的是哑节点
            if(pre.next.val == cur.next.val){
                //如果pre和cur指向的节点s值相等，那么就不断移动cur，直到pre和cur指向的值不相等
                while(cur.next!=null && pre.next.val==cur.next.val){
                    cur = cur.next;
                }
                
                pre.next = cur.next;
                cur = cur.next;
            }
            //如果当前节点与下一节点不重复，那么就让pre和cur两个节点同时往后移
            else{
                pre = pre.next;
                cur = cur.next;
            }
        }
        return dummy.next;
    }
}

11. arraylist的使用

arraylist逆序：Collections.reverse(arraylist);

arraylist最大值：Collections.max(arraylist);

或者用linkedlist存储，addFirst(int value);//从列表首部添加元素

addLast(int value);//从列表末尾添加元素

ArrayList转int[]：arraylist.stream().mapToInt(Integer::valueof).toArray();

ArrayList转String[]：arraylist.toArray(new String[size]);

arraylist删除节点：arraylist.remove(0);//去除第一个节点

12.二分查找

mid=(left+right)>>>1可能会超时，一般还是用mid=left+(right-left+1)/2

主要的思路就是左右边界向中间走，两边夹：while(left<right)，用于在循环体内排除元素，退出循环时left==right，区间[left,right]只剩下一个元素，那么这个元素可能就是我们要找的元素(target==nums[left]?left:-1)

常用的二分模板（升序数组找target）

    //在有序且升序的数组[0,mountainTop]中找target
   private int findFromSortedArr(MountainArray mountainArr, int left, int right, int target){
        while(left<right){
            int mid = left+(right-left)/2;
            //如果target>arr[mid],target在右边[mid+1, right]，因此需要更新左边界
            if(target>mountainArr.get(mid)){
                left = mid+1;
            }
            //如果target<arr[mid],target在左边[left, mid]
            else{
                right = mid;
            }
        }
        return mountainArr.get(left)==target ? left : -1;
    } 

山脉数组找顶点：如array = [1,2,3,4,5,3,1]，由于这种形式的数组应该是一个上升数组+一个下降数组构成，那么就要找到这两个数组的连接点

    private int findMountainTop(MountainArray mountainArr, int left, int right){
        while(left<right){
            int mid = left+(right-left)/2;
            //左边为上升数组，那么最大值在[mid+1,right]之间
            if(mountainArr.get(mid)<mountainArr.get(mid+1)){
                left = mid+1;
            }
            //左边有下降的部分，那么最大值在[left, mid]之间
            else{
                right = mid;
            }
        }
        return left;
    }

旋转数组（包含两个上升数组）找目标值，不存在相同元素的情况。将数组切分为两部分，只要是不是正好切分完，那么就可能存在只有一部分是上升数组，另外一部分是下降+上升数组。

    public int search(int[] nums, int target) {
        if(nums==null || nums.length==0){
            return -1;
        }
        int left = 0;
        int right = nums.length-1;
        while(left<right){
            int mid = left+(right-left)/2;
            //左边[left, mid]为升序序列。left=mid等于的情况即[6,0]，target=6
            if(nums[left]<=nums[mid]){
                //如果target在里面[left,mid]
                if(nums[left]<=target && target<=nums[mid]){
                    right = mid;
                }
                //如果不在这里，那么就在[mid+1,right]
                else{
                    left = mid+1;
                }
            }
            //即nums[left]>nums[mid],如[6,7,0,1,2,3,4,5]，右边[mid+1,right]为升序队列
            else{
                //如果target在右边[mid+1, right]
                if(nums[mid]<target && target<=nums[right]){
                     left = mid+1;
                }
                else{
                    right = mid;
                }
            }
        }
        return nums[left]==target ? left : -1;
    

升级版：找到旋转数组中的某个元素，数组原先是升序排列的，存在多个相同元素的情况。这个题需要考虑的有两种情况，如果能判断升序区间，根据目标值的大小移动边界；如果不能判断升序区间，清除重复值

因为在划分左右两端的时候，查找的元素可能同时存在于左右两边，如果有重复元素，那么就清除掉。

重复元素的出现情况：1.[5,6,7,1,2,3,5,5]，最右端和最左端重复，直接调整right，直至nums[left]!=nums[right]，也就是[5,6,7,1,2,3]

2.[5,6,7,1,1,2,3,4]，划分后[5,6,7,1]和[1,2,3,4]，中间元素重复。那么就调整mid，直到左右两侧的元素各不相同，如[5,6,7]和[1,1,2,3,4]

    public int search(int[] arr, int target) {
        if(arr==null || arr.length==0){
            return -1;
        }
        int left = 0;
        int right = arr.length-1;
        while(left<right){
            int mid = left+(right-left)/2;
            if(arr[left]==arr[right] && arr[left]==target){
                return left;
            }
            //[left,mid]升序
            //[7, 10, 14, 16, 19, 20, 25, 1, 3, 4, 5]
            if(arr[left]<arr[mid]){
                //target在左边升序区间[left,mid]，target=14
                if(arr[left]<=target && target<=arr[mid]){
                    right = mid;
                }
                else{
                    left = mid+1;
                }
            }
            //[mid,right]升序
            //[15, 16, 19, 20, 25, 1, 3, 4, 5, 7, 10, 14]
            else if(arr[left]>arr[mid]){
                //target在区间内[mid+1,right]
                //[5,5,5,1,2,3,4,5] target=5，arr[left]=target
                if(arr[mid]<target && target<=arr[right]){
                    left = mid+1;
                }
                else{
                    right = mid;
                }
            }
            //找到重复值/目标值，因为根据条件while(left<right)，左右两边会不断收拢，最终[left,right]区间只有一个值，所以如果不遇到重复值的情况下arr[left]==arr[mid]，仅当找到目标值了;如果有重复值，可能是找到的是重复值的情况         
            else if(arr[left]==arr[mid]){
                //去除重复值，下一轮搜索[left+1,right]
                if(arr[left]!=target){
                    left++;
                }
                //[2,1,2,2,2],target=2.mid的右边不一定是解，下一轮搜索应该在[left,mid]
                else{
                    return left;
                }
            }
        }
        return arr[left]==target ? left : -1;
    }

13.字符串切分：String[] c = s.split(" ");//只能匹配一个空格。String[] c = s.split("\\s+");//可以匹配任意个空格

14.合并两个升序链表

1）构建一个最小堆优先队列
2）把所有链表的头节点都放进去
3）出队当前优先队列中最小的节点，挂上链表
4）使得出队的节点的下一个节点入队
5）不断出队优先队列中最小的，直到优先队列为空

15.分成若干个小团体，该小团体的负责人将消息通知给他团体内的人。使用List<Integer>[] lists=new List[n]来描述这种关系

//manager[i]表示第i名员工的直属负责人
List<Integer>[] lists = new List[n];
for(int i=0; i<n; i++){
       lists[i] = new ArrayList<>();
}
for(int i=0; i<n ;i++){
       lists[manager[i]].add(i);
}

16.环的处理-拆分成两个队列

//leetcode 213
你是一个专业的小偷，计划偷窃沿街的房屋，每间房内都藏有一定的现金。这个地方所有的房屋都围成一圈，这意味着第一个房屋和最后一个房屋是紧挨着的。同时，相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/house-robber-ii
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

较不形成一个圈的房屋，需要进行的特殊处理就是：将这些房屋拆分成两个数组，一个数组[0,n-1]，另外一个数组[1,n]。即偷第一个，不偷最后一个&偷最后一个，不偷第一个。然后比较两个数组的最大值

17.很多看起来应该是用正则处理的题目，如果正则出不来，那么就可以考虑直接依次遍历输入的字符。e.g.jd20200917的java笔试题：提取一段英文文本中可能是年份的部分，1000-3999。首先看到这个题当然是考虑用正则，但是需要考虑数字与标点符号/空格/字母连在一起的情况，但是比如“02020”需要解析成为2020。那么解析起来就比较复杂，那么考虑直接使用输入的字符处理。“用一个int来记录当前可能为年份的值curYear，初始0。如果遇到的ch是数字，那么curYear = curYear * 10 + (ch-‘0’)；如果遇到的是非数字，判断当前的curYear是否在1000到3999之间，是的话打印，否则将curYear归零”。

18.归并排序

思路：先两两merge，完成一趟排序后，再四四merge，直到结束。

1.递归地将当前链表分为两段（fast-slow双指针）
2.递归地对前半段 和 后半段 进行归并排序
3.将两个已排好序的链表进行merge（merge时，将两段头部节点值比较，始终要p指向较小的一项。注意当一段指向null，那么处理另一段剩下的元素。注意设置一个dummy节点）

例：排序链表，（在O(nlogn)时间复杂度和常数级空间复杂度上，对链表进行排序）

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode sortList(ListNode head) {
        if(head==null){
            return null;
        }
        return mergeSort(head);
    }

    private ListNode mergeSort(ListNode head){
        if(head.next==null || head==null){
            return head;
        }
        //将当前链表分为两段-使用快慢指针
        ListNode p1=head, p2=head.next;
        while(p2!=null && p2.next!=null){
            p1 = p1.next;
            p2 = p2.next.next;
        }
        //对右半部分进行归并，中心节点p1的下一节点，链表从p1切断
        ListNode right = mergeSort(p1.next);
        //链表结束的标志，将链表切断
        p1.next = null;
        //对左半部分进行归并，当前链表左端点head
        ListNode left = mergeSort(head);
        return merge(left, right);
    }

    //合并链表
    private ListNode merge(ListNode left, ListNode right){
        ListNode dummy = new ListNode(0);
        ListNode cur = dummy;
        while(left!=null && right!=null){
            if(left.val < right.val){
                cur.next = left;
                left = left.next;
            }
            else{
                cur.next = right;
                right = right.next;
            }
            cur = cur.next;
        }
        //如果left还有剩余
        if(left != null){
            cur.next = left;
        }
        //如果right还有剩余
        if(right != null){
            cur.next = right;
        }
        return dummy.next;
    }

}

18.处理字符串

如果要处理字符串满足某种格式，那么怎么实现依次遍历，然后字符串中字符还需要前后比较呢？

考虑使用StringBuilder，首先把StringBuilder stb = new StringBuilder(String str);然后遍历stb中的每个字符，然后如果不符合条件需要删除当前字符：stb.deleteCharAt(i);i--;（注意要i--，因为原来的i应该被删除掉了，在for循环中默认有一个i++，所以为了防止会跳过这个字符，那么在删除的时候，需要往前移一位）

19.旅行商问题

https://www.nowcoder.com/questionTerminal/3d1adf0f16474c90b27a9954b71d125d

20.链表的操作

1）链表翻转

public ListNode reverseList(ListNode head){
        if(head==null) 
            return null;
        ListNode pre=null;
        ListNode next;
        //当 head 或者 next 指向 null 的时候，我们就可以停止了
        while(head!=null){
            next=head.next; //next指向head的next，防止原链表丢失
            head.next=pre; //head的next从原链表脱离，指向pre（新链表）.
            pre=head; //pre指向head，pre右移
            head=next; //head指向next，head右移
        }
        return pre; //返回pre，为逆序链表
    }

 

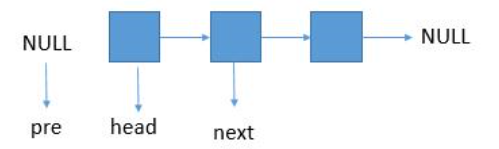
2）找链表的中点：快慢指针

ListNode slow = head, fast = head.next;
while(fast!=null && fast.next!=null){
       slow = slow.next;
       fast = fast.next.next;
}
slow;//中点
ListNode after = slow.next;//后半段链表
slow.next = null;

21.并查集问题：比如给定若干个同学，每两个同学是好朋友，若干个好朋友可以组成一个小团体，求最后有几个小团体。

模板：

int pre[1000];//记录每个点的前导点是什么，如pre[10]=2表示10号的前导点是2号
//查找根结点
int search(int root) 
{
    int son, tmp;
    son = root;
    //当当前节点的前导点还是当前节点时，当前节点为根节点。因为每个节点都只能找到它的前导点，所以为了找到根节点，只能一级级往上查
    while(root != pre[root]) 
        root = pre[root];
    //路径压缩，将所有的节点都将根节点作为前导点
    while(son != root) 
    {
        //改变上级之前，用临时变量记录它的值
        tmp = pre[son];
        //把当前节点的上级改为根节点
        pre[son] = root;
        son = tmp;
    }
    return root; 
}

//合并，将x和y在一起，就是在x和y这两个点上连一条线，这样，两个人所在的板块中的所有点就连通了
void join(int x, int y){
        int fx=search(x),fy=search(y);
        //如果x和y的前导点不一样，所以不连通，那么就把他们所在的前导点连通。前导点的相互关系没有影响
        if(fx!=fy){
             pre[fx]=fy;
        }       
}

模板怎么用？如上面的求小团体数目

search(){...}
join(){...}
int main(){
      //接收一共有多少个同学num，以及多少个好友关系的输入road
      int total = num-1;//初始化团体个数就是同学的个数
      //初始化i同学的前导点是自身
      for(int i=1; i<=num; i++){
            pre[i] = i;
      }
      while(road-->0){
            //接收建立好友关系的两个同学stu1,stu2
            //注意在连接时，进行连接时，需要total--，因为两部分连接，那么小团体就少一个
            join(stu1, stu2);

       }
}

22.单调栈求解图中最大矩形的问题

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。
求在该柱状图中，能够勾勒出来的矩形的最大面积。

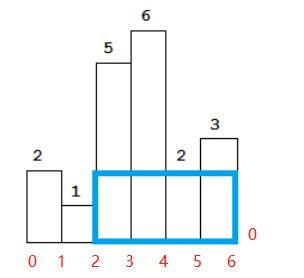
1）首先应该求能完全包含各个柱子的最大面积：如何求？矩形=宽*高，如果求包含第i个柱子的面积，首先高=第i个柱子的高，那么宽度？这个矩形的左边沿是左边第一个比第i个柱子小的柱子，右边沿是右边第一个比第i个柱子小的柱子。因此宽=矩形右边沿-（矩形左边沿+1），下图以包含第4个柱子（高度为2）为例

为什么要左边沿+1？因为左边沿是 左边第一个高度小于该柱子 的 右边

2）求最大面积的最大值

如果找左右边沿？当第i个柱子进栈时，栈顶柱子（需要完全包含的柱子）的高度低于或等于第i个柱子，那么第i个柱子进栈。如果高于第i个柱子，则出栈，并计算以栈顶柱子 为高的矩形最大面积（包含栈顶柱子的矩形）。此时左边沿=单调栈中紧邻栈顶柱子的柱子，右边沿=i（i是右边第一个矮于栈顶的柱子）

维护一个单调栈，使得栈中的元素始终保持递增

https://leetcode-cn.com/problems/largest-rectangle-in-histogram/solution/zhu-zhuang-tu-zhong-zui-da-de-ju-xing-by-leetcode-/

    public int largestRectangleArea(int[] heights) {
        int count = heights.length;
        Deque<Integer> stack = new LinkedList<>();
        //右边界为最后一个柱子时，方便计算
        stack.push(-1);
        int area = 0;
        for(int i=0; i<=count; i++){
            //如果栈顶柱子为空，那么将栈顶元素置0
            int cur = i<count?heights[i]:0;
            //小于栈顶高度时，说明找到了右边的第一个小于自身的柱体，将栈顶出栈来计算以栈顶为高的面积
            while(stack.peek()!=-1 && heights[stack.peek()]>cur){
                int temp = stack.pop();
                int weight = i-stack.peek()-1;
                area = Math.max(area, weight*heights[temp]);
            }
            //大于栈顶的高度时，将当前柱体入栈
            stack.push(i);
        }
        return area;
    }

23.数位dp（数位其实就是一个数有个、十、百、千...位，数的每一位就是数位）

问区间[left,right]中，满足某条件的所有数的个数。

将问题转化为：设ans[i]为在区间[1,i]中满足条件的数的数量，那么所求的答案是ans[right]-ans[left-1]

引入数位为了dp，其实就是暴力枚举，使得新的枚举方式满足dp，然后记忆化即可

即控制上界枚举，从高位向下枚举，如right=213，首先从百位（0，1，2），然后每一个枚举都不能让枚举的数超过上界213，所以当百位枚举1，那么十位可以0-9；百位枚举2，十位可以0-1；如果百十位枚举21，个位而只能0-3

搬运一个模板：

typedef long long ll;  
int a[20];  
ll dp[20][state];//不同题目状态不同  
ll dfs(int pos,/*state变量*/,bool lead/*前导零*/,bool limit/*数位上界变量*/)//不是每个题都要判断前导零  
{  
    //递归边界，既然是按位枚举，最低位是0，那么pos==-1说明这个数我枚举完了  
    if(pos==-1) return 1;/*这里一般返回1，表示你枚举的这个数是合法的，那么这里就需要你在枚举时必须每一位都要满足题目条件，也就是说当前枚举到pos位，一定要保证前面已经枚举的数位是合法的。不过具体题目不同或者写法不同的话不一定要返回1 */  
    //第二个就是记忆化(在此前可能不同题目还能有一些剪枝)  
    if(!limit && !lead && dp[pos][state]!=-1) return dp[pos][state];  
    /*常规写法都是在没有限制的条件记忆化，这里与下面记录状态是对应，具体为什么是有条件的记忆化后面会讲*/  
    int up=limit?a[pos]:9;//根据limit判断枚举的上界up;这个的例子前面用213讲过了  
    ll ans=0;  
    //开始计数  
    for(int i=0;i<=up;i++)//枚举，然后把不同情况的个数加到ans就可以了  
    {  
        if() ...  //修改部分
        else if()...//  
        ans+=dfs(pos-1,/*状态转移*/,lead && i==0,limit && i==a[pos]) //最后两个变量传参都是这样写的  
        /*这里还算比较灵活，不过做几个题就觉得这里也是套路了 
        大概就是说，我当前数位枚举的数是i，然后根据题目的约束条件分类讨论 
        去计算不同情况下的个数，还有要根据state变量来保证i的合法性，比如题目 
        要求数位上不能有62连续出现,那么就是state就是要保存前一位pre,然后分类， 
        前一位如果是6那么这意味就不能是2，这里一定要保存枚举的这个数是合法*/  
    }  
    //计算完，记录状态  
    if(!limit && !lead) dp[pos][state]=ans;  
    /*这里对应上面的记忆化，在一定条件下时记录，保证一致性，当然如果约束条件不需要考虑lead，这里就是lead就完全不用考虑了*/  
    return ans;  
}  
ll solve(ll x)  
{  
    int pos=0;  
    while(x)//把数位都分解出来  
    {  
        a[pos++]=x%10;//个人老是喜欢编号为[0,pos),看不惯的就按自己习惯来，反正注意数位边界就行  
        x/=10;  
    }  
    return dfs(pos-1/*从最高位开始枚举*/,/*一系列状态 */,true,true);//刚开始最高位都是有限制并且有前导零的，显然比最高位还要高的一位视为0嘛  
}  
int main()  
{  
    ll le,ri;  
    while(~scanf("%lld%lld",&le,&ri))  
    {  
        //初始化dp数组为-1,这里还有更加优美的优化,后面讲  
        printf("%lld\n",solve(ri)-solve(le-1));  
    }  
}  
 

如不要62这个题，那么就需要把模板中的修改部分改为：且dfs(int pos, int pre, int state,bool limit)，因为62需要判断前面的值是否为6，所以用pre来记录

for(int i=0;i<=up;i++){
        if(i == 4) continue;
        else if(pre == 6 && i == 2) continue;
        ans+=dfs(pos-1, i, i == 6 ? 1 : 0, limit && i==a[pos]);
}

24.旋转数组找最小值，二分法，不断让nums[mid]和nums[right]比较，为什么不让nums[mid]和nums[left]比较呢？

 因为nums[left]<nums[mid]时，无法判断mid在哪个排序数组中。因为由于是两个升序数组构成的旋转数组，那么nums[right]初始值一定是在右排序数组中，但是如果旋转点是0，即是一个升序数组，那么nums[left]初始值无法确定是在哪个升序数组中，因此无法缩小范围。

二分的目的是判断mid在哪个排序数组中。如left=0,right=4,mid=2时，对数组[1,2,3,4,5]和数组[3,4,5,1,2]，都有nums[mid]>nums[left]，但对于前者mid在右排序数组中，后者mid在左排序数组中

class Solution {
    public int minArray(int[] numbers) {
        int left = 0, right = numbers.length-1;
        while(left<right){
            int mid = left+(right-left)/2;
            //如果nums[mid]<nums[right]，说明右边为完整的上升数组，最小值在[left, mid]
            if(numbers[mid]<numbers[right]){
                right = mid;
            }
            //如果nums[mid]>nums[right]，右边为升序+升序，最小值在(mid, right]
            else if(numbers[mid]>numbers[right]){
                left = mid+1;
            }
            //如果相等，去重
            else{
                right--;
            }
        }
        return numbers[left];
    }
}