leetcode-课程表
课程表I
你这个学期必须选修 numCourse 门课程,记为 0 到 numCourse-1 。 在选修某些课程之前需要一些先修课程。 例如,想要学习课程 0 ,你需要先完成课程 1 ,我们用一个匹配来表示他们:[0,1] 给定课程总量以及它们的先决条件,请你判断是否可能完成所有课程的学习?
题解
class Solution { public boolean canFinish(int numCourses, int[][] prerequisites) { //构建入度表 int[] indegrees = new int[numCourses]; //构建邻接表 List<List<Integer>> adjacency = new ArrayList<>(); for(int i=0; i<numCourses; i++){ adjacency.add(new ArrayList<>()); } //构建队列 Queue<Integer> queue = new LinkedList<>(); //对每门课程 设置其对应的入度和邻接表(存放后继successor结点的集合) //想要学习课程0,先要完成课程1,表示为[0,1] for(int[] course : prerequisites){ //因为course[0]之前先要学习course[1],所以course[0]入度++ indegrees[course[0]]++; //key:课的编号,value:依赖它的后续课程(数组) adjacency.get(course[1]).add(course[0]); } //将所有入度为0的节点入队 for(int i=0; i<numCourses; i++){ if(indegrees[i] == 0){ queue.add(i); } } //当queue非空,依次将队首节点出队,邻接表中删除此节点 while(!queue.isEmpty()){ int pre = queue.poll(); numCourses--; //学习了pre课程,cure为接下来邻接的课程,即接下来学习的课程。 //遍历每一个邻接节点 for(int cur:adjacency.get(pre)){ //当入度-1,邻接节点cur的入度=0,则说明cur所有前驱节点都被删除,此时cur入队 if(--indegrees[cur] == 0){ queue.add(cur); } } } //即拓扑排序出队次数等于课程数 return numCourses==0; } }
思路
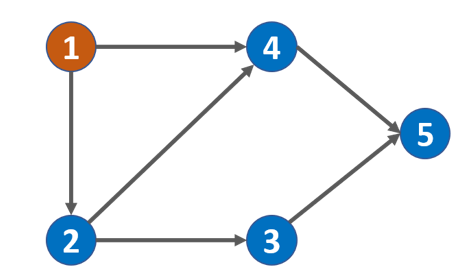
将题目简化为“课程安排表是否为无环有向图”(通过拓扑排序判断),如果是DAG,那么课程间规定了前置条件。
对DAG的顶点排序,使得对每一条有向边(u,v),u比v更显出现。如上图,上课程2,必须完成课程1;上课程4,必须完成课程2和1
通过课程条件表输入,可以得到课程安排图的邻接表。然后通过广度优先遍历解决。
1.首先统计课程条件表中每个节点的入度(即每门课程当前需要上几门课,如上图的课程1的入度为0,课程2的入度为1),生成入度表
2.借助一个队列用来存储所有入度为0的节点
3.遍历课程表中的每一个节点,构建入度表和邻接表
4.当队列非空时,依次将队首节点出队,然后在邻接表中删除该节点。表示学习该课程,遍历接下来的课程,表示学习其他的课程,那么如果接下来的课程入度为0(需要--课程入度,因为此时课程的前导课刚刚学完),就将该课程入队,说明接下来就学习该课程。并且执行numCourses--,若整个课程表为有向无环图,所有的节点都一定入队和出队,完成拓扑排序。
5.当遍历完,numCourses不为0,即还有节点没有入队和出队,那么说明该课程不能成功安排。
课程表II
现在你总共有 n 门课需要选,记为 0 到 n-1。 在选修某些课程之前需要一些先修课程。 例如,想要学习课程 0 ,你需要先完成课程 1 ,我们用一个匹配来表示他们: [0,1] 给定课程总量以及它们的先决条件,返回你为了学完所有课程所安排的学习顺序。 可能会有多个正确的顺序,你只要返回一种就可以了。如果不可能完成所有课程,返回一个空数组。
题解
class Solution { public int[] findOrder(int numCourses, int[][] prerequisites) { //队列存储入度=0的节点 Queue<Integer> queue = new LinkedList<>(); //构建邻接表 List<List<Integer>> adjacent = new ArrayList<>(); for(int i=0; i<numCourses; i++){ adjacent.add(new ArrayList<>()); } //构建入度表 int[] indegrees = new int[numCourses]; for(int[] courseCouples:prerequisites){ indegrees[courseCouples[0]]++; adjacent.get(courseCouples[1]).add(courseCouples[0]); } //将入度=0的课程,入队 for(int i=0; i<numCourses; i++){ if(indegrees[i]==0){ queue.add(i); } } //构建返回的课程表 int[] ret = new int[numCourses]; int count=0; //遍历 while(!queue.isEmpty()){ int pre = queue.poll(); ret[count++]=pre; for(int cur:adjacent.get(pre)){ if(--indegrees[cur]==0){ queue.add(cur); } } } return count==numCourses?ret:new int[0]; } }
这个与上一题的差别在于,这里记录课程的学习顺序。
扩展
通过DFS(深度优先遍历也可以判断图中是否有环)
class Solution { public boolean canFinish(int numCourses, int[][] prerequisites) { List<List<Integer>> adjacency = new ArrayList<>(); for(int i = 0; i < numCourses; i++) adjacency.add(new ArrayList<>()); //构建一个标志列表,判断每个节点的状态。每个节点表示一门课程,默认为0,即未被DFS访问 int[] flags = new int[numCourses]; for(int[] courses : prerequisites) adjacency.get(courses [1]).add(courses [0]); //对每个节点依次执行DFS,判断每个节点起步DFS是否存在环 for(int i = 0; i < numCourses; i++) if(!dfs(adjacency, flags, i)) return false; //若整个图DFS结束,也没有环 return true; } private boolean dfs(List<List<Integer>> adjacency, int[] flags, int i) { //若flags[i]==1,则已被当前节点启动的DFS访问,即本轮DFS搜索中,当前节点已经被第二次访问,即有环 if(flags[i] == 1) return false; //若flags[i]==-1,则已被其他节点启动的DFS访问,无需再重复搜索 if(flags[i] == -1) return true; //否则flag=0,说明该节点之前没有被访问过,那么第一次访问=1 flags[i] = 1; //遍历当前节点的邻接节点,判断是否有环 for(Integer j : adjacency.get(i)) if(!dfs(adjacency, flags, j)) return false; //当前节点所有邻接节点已被遍历,并没有发现环,则将该节点置为-1 flags[i] = -1; return true; } }
课程表III
这里有 n 门不同的在线课程,他们按从 1 到 n 编号。每一门课程有一定的持续上课时间(课程时间)t 以及关闭时间第 d 天。一门课要持续学习 t 天直到第 d 天时要完成,你将会从第 1 天开始。 给出 n 个在线课程用 (t, d) 对表示。你的任务是找出最多可以修几门课。
题解
class Solution { public int scheduleCourse(int[][] courses) { //按课程结束时间升序 Arrays.sort(courses, (a,b)->(a[1]-b[1]));
//课程用时的大根优先级 Queue<Integer> queue = new PriorityQueue<>( (a,b)->(b-a)); //总用时 int times=0; for(int i=0; i<courses.length; i++){
//如果该课程可以学习(学习时长合适),则学习。总时长增加,课程入堆 if(times+courses[i][0]<=courses[i][1]){ times+=courses[i][0]; queue.add(courses[i][0]); }
//如果该课程不能学习,因为此课程的结束时间比之前所有的都晚。 else{
//先把该课程加上 queue.add(courses[i][0]); //放弃之前用时最长的课程,如果当前课程是最长用时,那么放弃当前课程(此课程比之前课程用时多,不学该课程)
//放弃之前用时最长的课程(此课程比之前课程用时少,学该课程) times=times+courses[i][0]-queue.poll(); } } return queue.size(); } }
思路
贪心算法
按照课程结束时间排序?因为课程持续时间并不能保证 当对课程遍历时每个课程都是合法的。先学习结束时间最靠前的最好,理想的情况是:所有前一门课程的结束时间和下一门课程的开始时间都不相交(目前用时+课程时长<课程关闭时间),那么就可以学习所有课程。
一旦发现安排了当前课程之后,其结束时间超过最晚结束时间,那么就从已安排的课程中,取消掉当前最耗时的一门课程
举例:
如[[4,6],[5,5],[2,6]]
按照课程结束时间排序,[[5,5],[4,6],[2,6]]
课程的起始时间为0,首先选择课程1:[5,5],那么当前已选课程为[[5,5]]
课程的起始时间为5,接着选择课程2:[4,6],那么如果选择学习课程2,持续时间4+当前起始时间5=9>要求的结束时间6,因此不可取。
那么对于这两门课程,无论怎么选择,都只能选择其中的一门课程。
那么肯定是选择这两门课程耗时更短的课程,因为当前起始时间相同,如果该课程耗时更短,那么该课程也会更早结束,那么留给其他课程的时间会更宽裕。课程2[4,6]的耗时小于课程1[5,5],那么就用课程2替换掉课程1。
先把该课程加上,已选课程为[[5,5],[4,6]]
当前起始时间就变为5+4-5(耗时更长的课程)=4,那么当前已选课程为[[4,6]]
再考虑课程3[2,6],当前起始时间为4,那么如果学习课程3,持续时间2+当前起始时间4=要求的结束时间6,那么就可以学该课程,把课程加上,并且当前起始时间=6
所以queue中的课程为[[4,6],[2,6]],size=2



 浙公网安备 33010602011771号
浙公网安备 33010602011771号