Matlab 实现CZT

全通滤波器

b = [1 -1/0.9]; a=[1 -0.9];
[Fh,w] = freqz(b,a);
[Gd,w] = grpdelay(b,a);
subplot(311)
plot(w/pi,abs(Fh));ylabel('|H(w)|');grid on;
axis([0 max(w/pi) 0 1.5]);
subplot(312)
plot(w/pi,angle(Fh));
ylabel('ang[H(w)]');grid on;
subplot(313)
plot(w/pi,Gd);ylabel('grd[H(w)]');grid on;

$$H(z) = \frac{1-\frac{1}{0.9}z^{-1}}{1-0.9z^{-1}}$$

Matlab 实现CZT

h = firl(40,0.3); %h(n)为截止频率为0.3pi的40阶低通滤波器
fs = 1000;f1 = 100; f2 = 200;%fs = 1000Hz, fc = 150Hz
m = 1024;
w = exp(-j*2*pi*(f2-f1)/(m*fs));
a = exp(j*2*pi*f1/fs);

H = fft(h,1000);
H1 = czt(h,m,w,a);
%CZT长度：M=1024，希望通过CZT看清楚过渡带
fH = (0:length(H)-1)'*1000/length(H);
fH1 = (0:length(H1)-1)'*(f2-f1)/length(H1)+f1;

$$W = W_0e^{-j\phi_0} \\ W_0 = 1\ \ \phi_0 = (\omega_2-\omega_1)/M \\ \omega_* = 2\pi \frac{f_*}{f_s} \\ W = e^{-j\frac{2\pi}{Mf_s}(f_2-f1)}\\ A = A_0e^{j\theta_0}=e^{j\frac{j2\pi}{f_s}(f_1)}$$

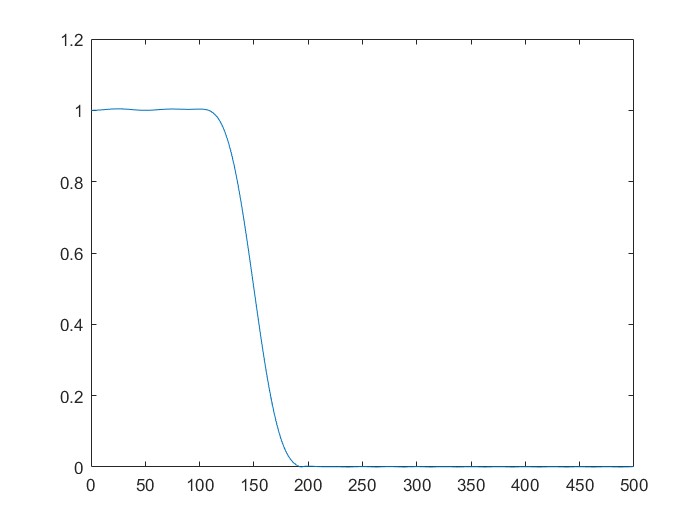
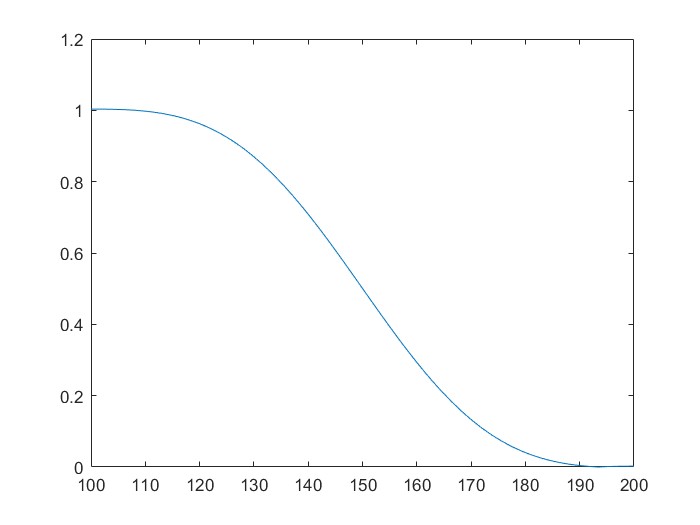
所以CZT能让我们更好的观察100-200HZ这个频段

模拟低通滤波器

数字滤波器：

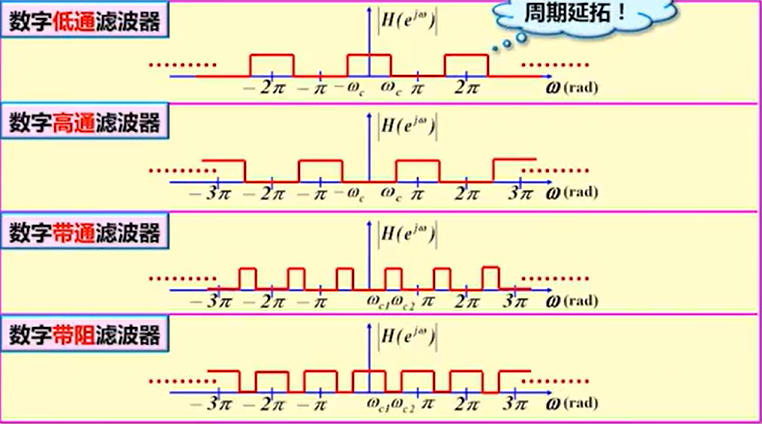
所以观察的范围在[0,Π]空间范围