dspLearning_频率响应的意义以及简单滤波器的设计
频率响应的意义
n = 0.:199;%取两百个点
x = sin(0.01*pi*n); %2pi/T = omega = 0.01pi,故T=200(所以一个周期采样了200个点)
b = [0.05,0.05]; a = [1,-0.9]; %b是系统响应z变换的分子系数 a是分母系数
y = filter(b,a,x); %求解差分方程
figure(1);%第一个图像
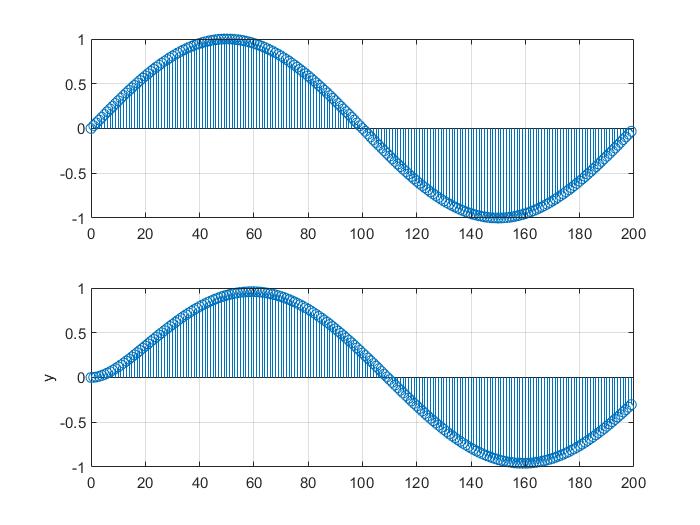
subplot(2,1,1);ylabel('x');
stem(n,x);grid on;
subplot(2,1,2);ylabel('x')
stem(n,y);grid on;ylabel('y');
figure(2);
[Fh,w] = freqz(b,a); %求系统的频率响应
[Gd,w] = grpdelay(b,a); %grpdelay表示群延迟
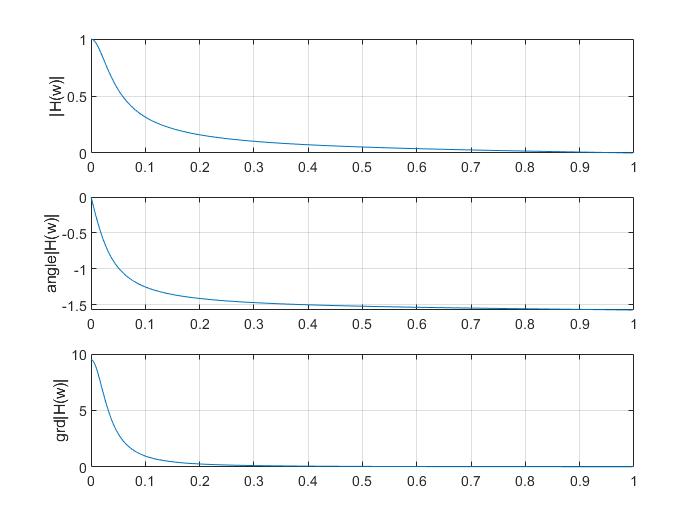
subplot(311); %幅度响应
plot(w/pi,abs(Fh));ylabel('|H(w)|');grid on;
subplot(312); %相位响应
plot(w/pi,angle(Fh));ylabel('angle|H(w)|');grid on;
subplot(313);%群延迟
plot(w/pi,Gd);ylabel('grd|H(w)|');grid on;
3点均值滤波系统
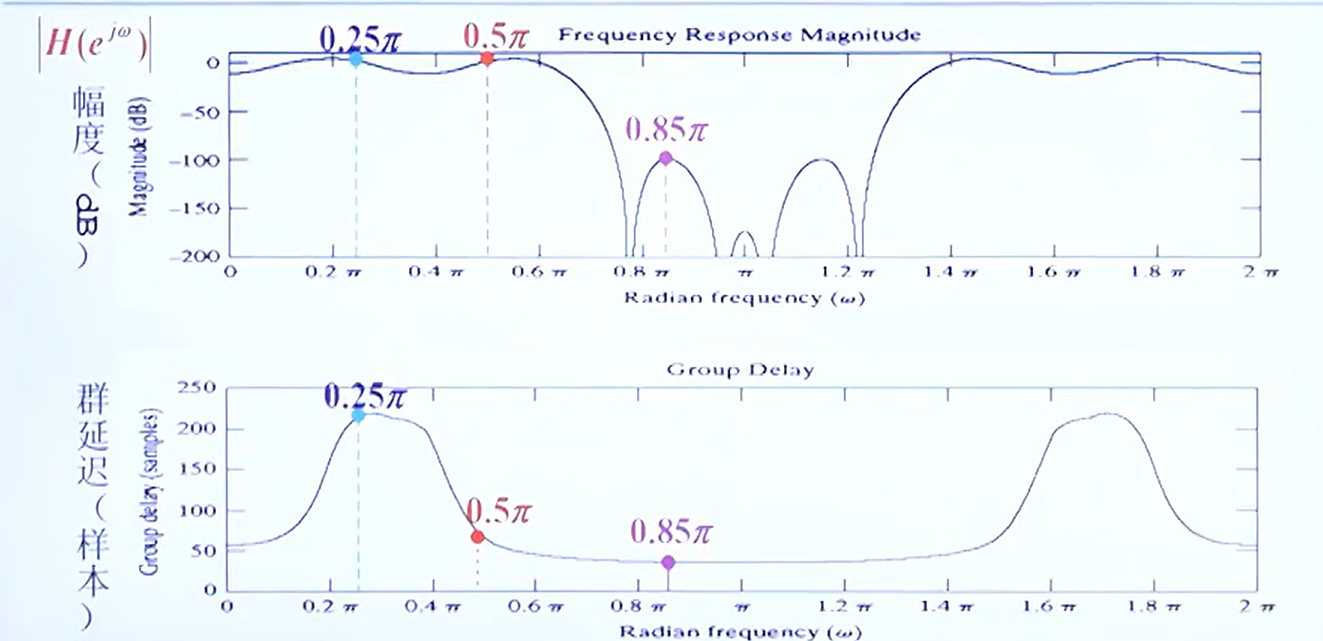
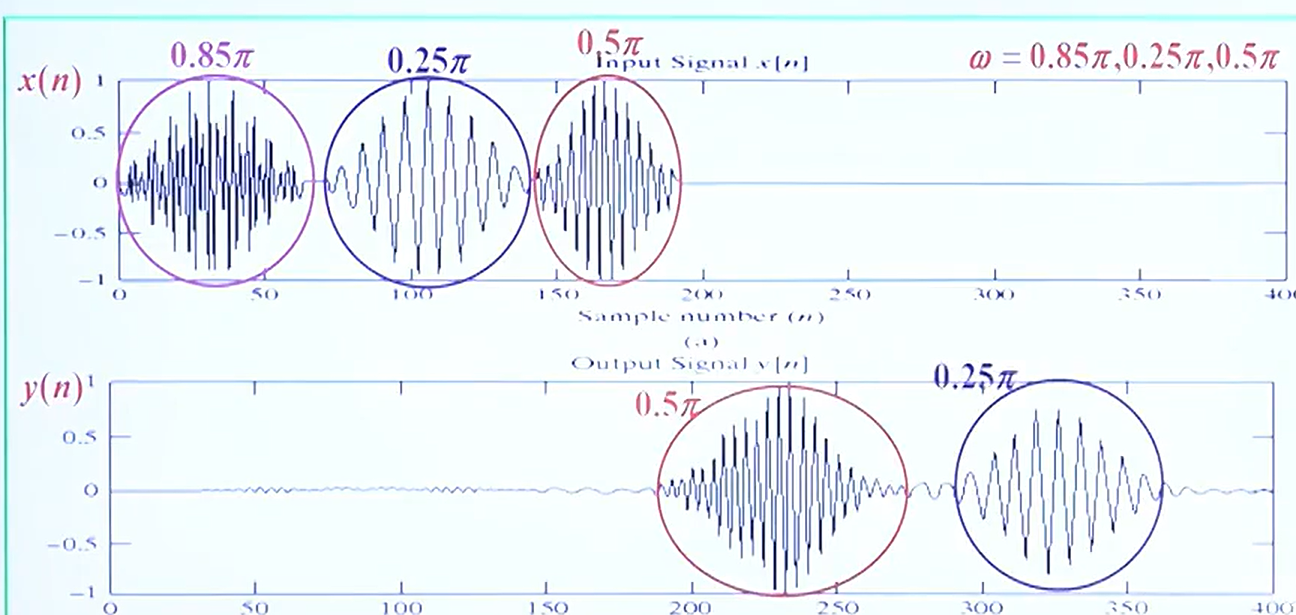
简单一阶滤波器的设计
b = [0.05 0.05]; %构造系统函数
a = [1 -0.9];
n = [0:99];
N = 100;fs = 1000;
x = sin(2*pi*10*n/fs)+sin(2*pi*250*n/fs); %构造两个频率成分 一个10Hz,一个250Hz,采样频率fs = 1000Hz
y = filter(b,a,x); %求系统输出
figure(1) %先画好画板
zplane(b,a);%画零极点图
figure(2)
subplot(211);plot(n,x);%画输入
subplot(212);plot(n,y);%画输出
figure(3)
Fx = fft(x);%画输入x(n)的频谱
subplot(311);
plot(n*fs/N,abs(Fx)/max(abs(Fx)));%Fx的频谱
[Hh,wh] = freqz(b,a,'whole');%画系统h(n)的频谱
subplot(312);plot(wh/pi,abs(Hh));
Fy = fft(y);
subplot(313);%画输出的频谱
plot(n*fs/N,abs(Fy)/max(abs(Fy)));
零极点图:
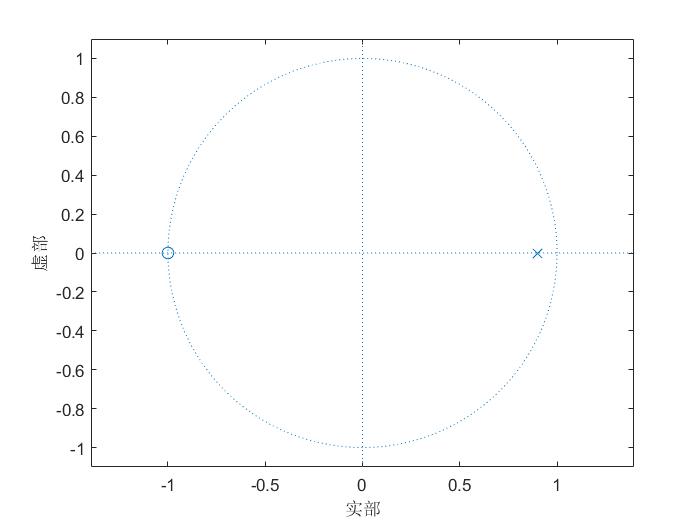
输入输出时域:
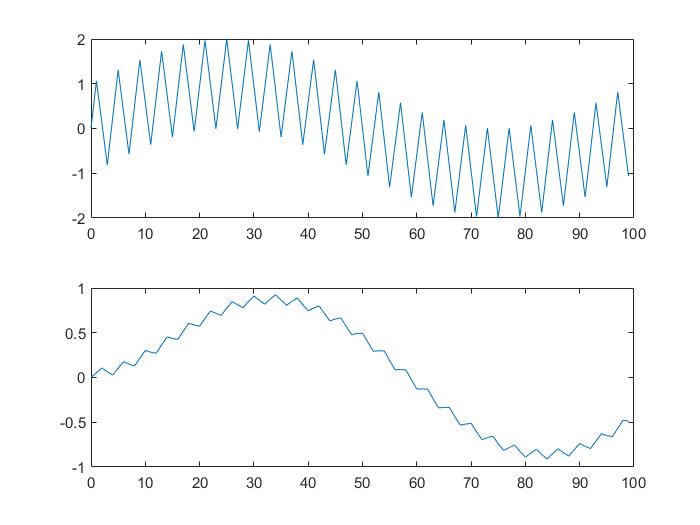
输入输出频域:
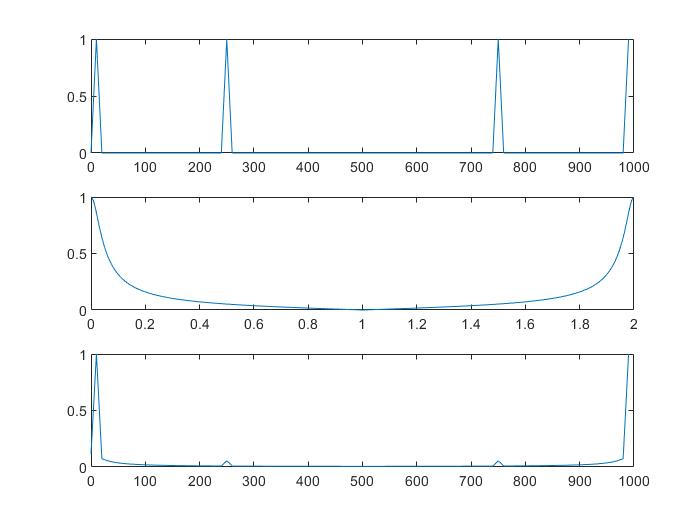
分类:
数字信号处理的matlba实现




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· TypeScript + Deepseek 打造卜卦网站:技术与玄学的结合
· Manus的开源复刻OpenManus初探
· AI 智能体引爆开源社区「GitHub 热点速览」
· 三行代码完成国际化适配,妙~啊~
· .NET Core 中如何实现缓存的预热?