DSPLearning_dayONE___________matlab实现DTFT里面的一些常用函数以及基本运算

DSP matlab实现

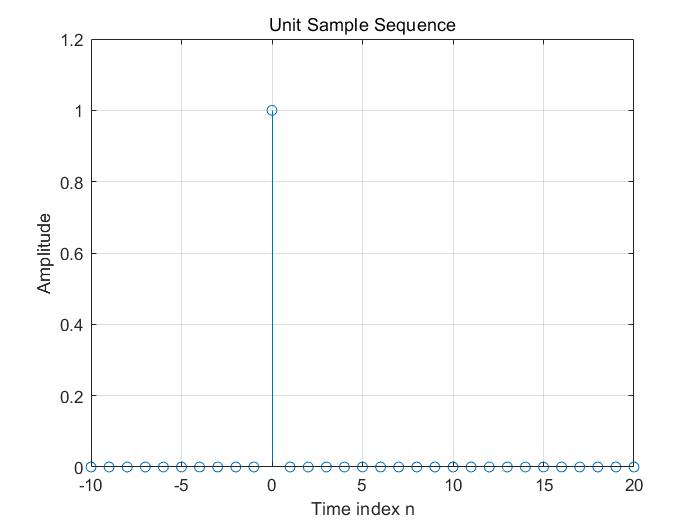
\(\delta(n)\)的实现

%matlab中坐标轴的横坐标和纵坐标是分开表示的
n = -10:20;  %横坐标的显示范围   这个是确定了x轴的坐标范围
delta = [zeros(1,10) 1 zeros(1,20)];%zeros(m,n)产生一个mxn的全零矩阵    这个是每个x轴对应的y轴的值
stem(n,delta); grid on; %画出delta(n),并在图中显示网格   这个是以stem函数来绘制
%%%%%%%%%%%%%%%这个部分是画图%%%%%%%%%%%%%%%%%%%%%%

xlabel('Time index n'); ylabel('Amplitude'); %横坐标和纵坐标的标识
title('Unit Sample Sequence');%图名
axis([-10 20 0 1.2]);   %axis([minX maxX minY maxY])
%%所以总的流程可以看成是：
%先给出坐标点（x，y），其中x和y分别都是向量，分别对应上面的n和delta
%然后确定用什么函数来表示这些点
%画图先定义x，y轴的坐标标识
%再定义图名和图像表示的范围

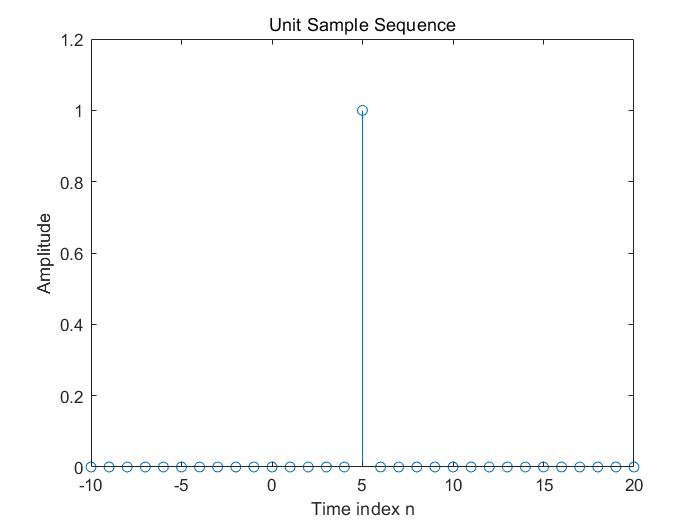
定义函数$\delta (n-np) $

%%%%%实现delta(n-np)     x(n)=delta(n-np),n \in [ns,nf]
function [x,n] = impseq(np,ns,nf)   %np 表示你在哪个位置上是1？， ns-nf是起始位置到终止位置，n：ns-nf，
%检查输入参数的正确性
if(( np < ns ) | ( np > nf) | ( ns > nf))
    error('参数必须满足 ns <= np <= nf')
end
%生成序列横坐标
n = [ns:nf];
%生成序列纵坐标
x=[(n-np) ==0];

%%所以实现一个函数的过程可以分解成：
%%function [返回值（这里有几个返回值，下面就要定义几个返回值）] = 函数名（一般和文件名相同）（参数表）
%根据参数表实现约束条件
%对每个返回值进行定义

调用函数

[x,n]=impseq(5,-10,20);
stem(n,x);
xlabel('Time index n'); ylabel('Amplitude'); %横坐标和纵坐标的标识
title('Unit Sample Sequence');%图名
axis([-10 20 0 1.2]);   %axis([minX maxX minY maxY])

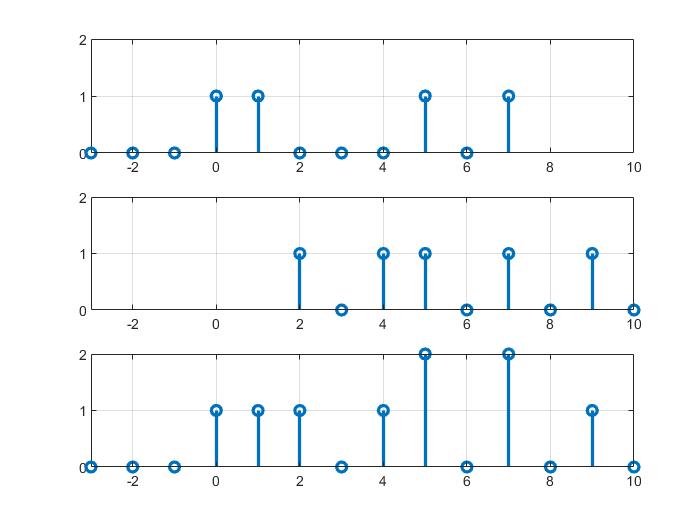
序列的相加

function [y,n] = seqadd(x1,n1,x2,n2) %matlab中横纵坐标都是分开的
n = min(min(n1),min(n2)):max(max(n1),max(n2)); %确定n的范围，分别是两个取值范围的并集
y1 = zeros(1,length((n)));%y1和y2都具有最终的相同的长度n
y2 = y1;
%把x1的值放到y1中，位置保持好
y1((n >=min(n1)) & (n <= max((n1)))) = x1;
%把x2的值放到y2中，位置保持好
y2((n >=min(n2)) & (n <= max((n2)))) = x2;
%将等长序列y1和y2相加
y = y1+y2;

实现

clear all;
clc;

n1 = -3:7;
n2 = 2:10;
x1=[0 0 0 1 1 0 0 0 1 0 1];
x2 = [1 0 1 1 0 1 0 1 0 ];
[y,n] = seqadd(x1,n1,x2,n2);
subplot(311);stem(n1,x1,'linewidth',2); #linewidth是表示宽度
axis([min(n) max(n) 0 max(y)]); grid on;#这个是显示图表的横纵坐标
subplot(312);stem(n2,x2,'linewidth',2);
axis([min(n) max(n) 0 max(y)]); grid on;
subplot(313);stem(n,y,'linewidth',2);
axis([min(n) max(n) 0 max(y)]); grid on;

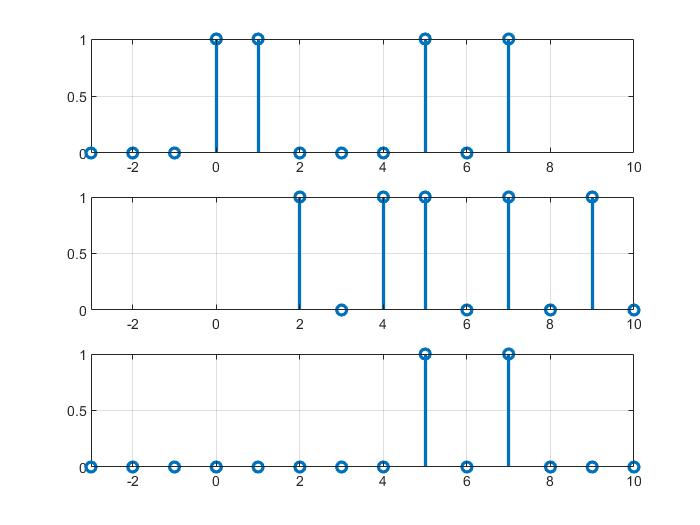
序列的乘积

function [y,n] = seqmult(x1,n1,x2,n2) %matlab中横纵坐标都是分开的
n = min(min(n1),min(n2)):max(max(n1),max(n2)); %确定n的范围，分别是两个取值范围的并集
y1 = zeros(1,length((n)));%y1和y2都具有最终的相同的长度n
y2 = y1;
%把x1的值放到y1中，位置保持好
y1((n >=min(n1)) & (n <= max((n1)))) = x1;
%把x2的值放到y2中，位置保持好
y2((n >=min(n2)) & (n <= max((n2)))) = x2;
%将等长序列y1和y2相乘
y = y1.*y2;

函数的调用

clear all;
clc;

n1 = -3:7;
n2 = 2:10;
x1=[0 0 0 1 1 0 0 0 1 0 1];
x2 = [1 0 1 1 0 1 0 1 0 ];
[y,n] = seqmult(x1,n1,x2,n2);
subplot(311);stem(n1,x1,'linewidth',2);
axis([min(n) max(n) 0 max(y)]); grid on;
subplot(312);stem(n2,x2,'linewidth',2);
axis([min(n) max(n) 0 max(y)]); grid on;
subplot(313);stem(n,y,'linewidth',2);
axis([min(n) max(n) 0 max(y)]); grid on;

序列的移位

function [y,ny] = seqshift(x,nx,m)%其中，x表示原序列，nx是其横坐标，m是移位量
ny = nx+m;
y = x;

移位的实现

clear all;
clc;

nx = -3:7;
x=[0 0 0 1 1 0 0 0 1 0 1];
m = 3;
[y,ny] = seqshift(x,nx,m);
subplot(211);stem(nx,x,'linewidth',2);
axis([min(min(nx),min(ny)) max(max(nx),max(ny)) 0 max(y)]); grid on;
subplot(212);stem(ny,y,'linewidth',2);
axis([min(min(nx),min(ny)) max(max(nx),max(ny)) 0 max(y)]); grid on;

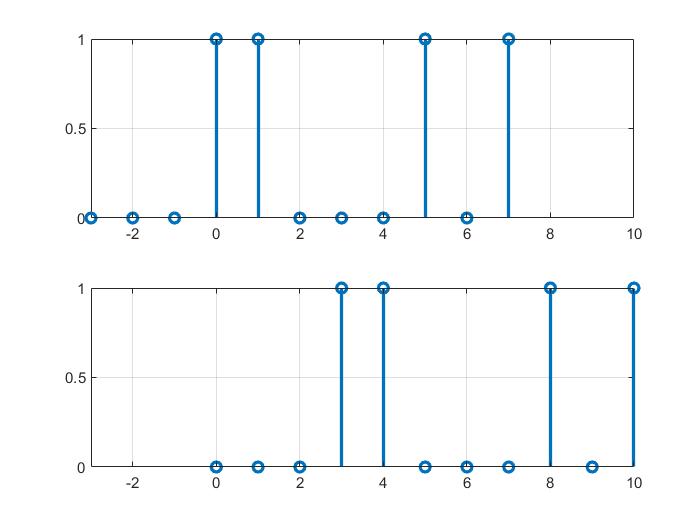
序列的翻褶

function [y,n] = seqfold(x,n)
y = fliplr(x);
n = -fliplr(n);
%matlab提供了翻褶函数：fliplr和plipud(x)
%行向量翻褶函数:fliplr(x)
%列向量翻褶函数:flipud(x)

翻褶的实现

clear all;
clc;

nx = -3:7;
x=[0 0 0 1 1 0 0 0 1 0 1];

[y,ny] = seqfold(x,nx);
subplot(211);stem(nx,x,'linewidth',2);
axis([min(min(nx),min(ny)) max(max(nx),max(ny)) 0 max(y)]); grid on;
subplot(212);stem(ny,y,'linewidth',2);
axis([min(min(nx),min(ny)) max(max(nx),max(ny)) 0 max(y)]); grid on;

音频文件的读取

[x,fs] = wavread(filename);  %两个音频读取函数
[x,fs] = audioread(filename);  %返回值是x:序列值，      fs：采样频率
%filename :给出.wav音频文件名 ，
%如果x是音频值，如果是单通道音频，则x是一个nx1的向量
%如果是双通道音频，则x是一个nx2的向量
%%%%%%%音频写入函数
wavwrite(y,fs,filename);
audiowrite(filename,y,fs);
y是要存入的音频值，fs是采样频率

音频反褶实现

[x,fs] = wavread('w2.wav'); %读入单声道音频文件
y = flipud(x); %反褶
figure(1);plot(x);grid on; 画图显示
figure(2);plot(y);grid on; 画图显示
wavwrite(y,fs,'w4.wav');结果保存为声音文件

正弦序列的实现

\[x(n) = Asin(n \omega + \phi)\\ x(n) = Acos(n \omega + \phi) \]

其中

\[sin(\Omega t)|_{t=nT} = sin(\Omega n T) = sin(n \omega) \]

• \(\omega ：\)数字角频率
• $\Omega: $ 模拟角频率
• \(T:\) 采样间隔

\[\omega = \Omega T \\ \omega = \frac{2\pi}{T_0}T = 2\pi \frac{f_0}{f} \]

n = 0:40;
x = 1.5*cos(0.2*pi*n);
stem(n,x);
axis([0 40 -2 2]); grid on;
title('Sinusoidal Sequence');
xlabel('Time index n');
ylabel('Amplitude x');

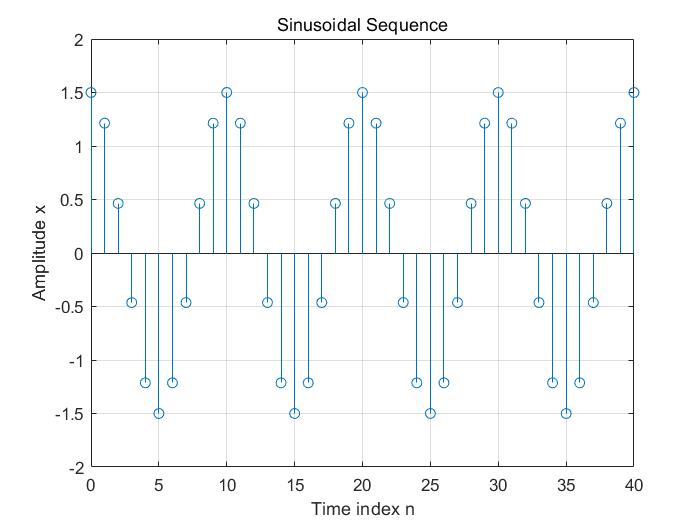
图中可以看出0.2 $\pi $ ,的含义：即

\[\omega = 0.2 \pi \\ \omega = \frac{2\pi}{T_0}T \\ T_0 = 10 T \]

所以一个周期采样10个点,这个就是实际含义

复数指数序列的实现

\[x(n) = e^{(\sigma+j\omega)n} = e^{\sigma n[cos\omega n +j sin\omega n]} \]

证明：(通过欧拉公式证明)

\[e^{\pm ix}=cosx \pm isinx \\ e^x = 1+\frac{x}{1!}+\frac{x^2}{2!}+\frac{x^3}{3!}+\cdots \\ cosx = 1-\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^6}{6!}+\cdots \\ sinx = x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+\cdots \\ e^{\pm ix} = 1\pm \frac{ix}{1!}-\frac{x^2}{2!} \mp\frac{ix^3}{3!}+\frac{x^4}{4!}+\cdots=(1-\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^6}{6!}+\cdots) \pm i(x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+\cdots)= \\ cosx \pm isinx \]

\[ \]

k = 2; n =0:40;
c = -(1/12)+(pi/6)* 1i ;
x = k*exp(c*n);
subplot(3,1,1); stem(n,real(x));
grid on; title('Real part');
subplot(3,1,2); stem(n,imag(x));
grid on; title('Imaginary part');
subplot(3,1,3); stem(n,abs(x));
grid on; title('Amplitude part');

$x(n) = 2e^{(-\frac{1}{12}+j\frac{\pi}{6})n} $

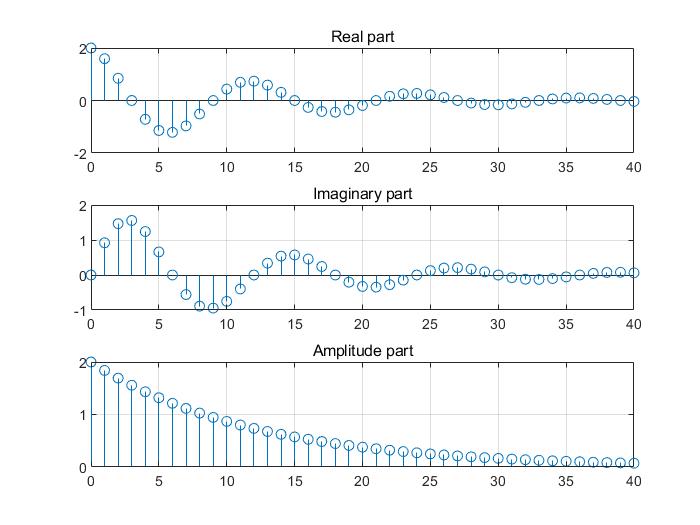
%随机序列的产生
x = rand(n); %x为nxn的均匀分布的随机矩阵，随机值的区间在(0,1)之间
x = rand(m,n);%x为mxn的均匀分布的随机矩阵，随机值的区间在(0,1)之间
%生成零均值单位方差的正态分布的随机信号
x = randn(n); %x为nxn的零均值单位方差正态分布的随机矩阵
x = randn(m,n); %x 为mxn的零均值单位方差正态分布的随机矩阵