面试题 - 二输入比较器实现排序算法
面试题 - 二输入比较器实现排序算法
@(数字集成电路基础)
1. 问题描述
给定8个数，以及若干二输入的比较器（可以将两个输入排序）。要求在单周期内实现8个数的排序，并使用最少的比较器个数。（乐鑫）
（距离面试已经过了很久，抽空整理一下当时的题目）
2. 问题解析
乍一看，排序算法，这不是个算法题么，将8个数排下序，脑子里最先出来的是什么冒泡，选择，插入排序......赶紧打住，我们现在在讨论电路，不要走错片场了。实际上题目限定了二输入的比较器，所以方向很明确，现在已经有二输入排序模块，我们要用这个二输入的模块搭成8输入的。那么自然也就能想到，先搭个4输入的，看有没有什么规律。
现在问题简化为4输入排序，很自然就想到，先分两组，每组之间排一下：（*表示较大的输出）
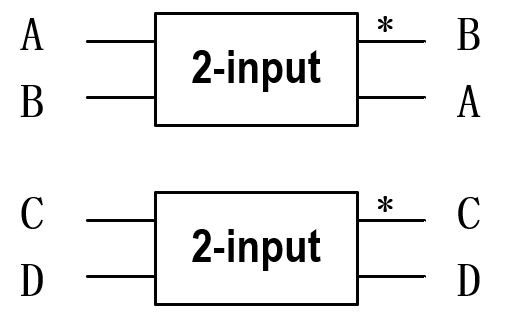
这样排完以后要解决的问题就是组间的大小问题。首先，两组之间最大的比较一下就能出来四个中最大的，两组最小的比较出来四个中最小的。所以第二级比较又需要两个比较器。第二级结束后我们已经得到了最大和最小，但次大和次小还不能确定，所以需要一个额外的比较器确定次大次小。
所以四个数的排序电路如下：
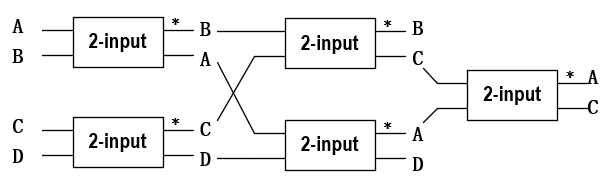
所以4个数进行排序需要的最少的二输入比较器个数是5个。
那么现在问题回到8个数，实际上我们相当于已经有了4输入进行排序的模块，用若干个4输入排序模块来完成8输入排序。相对于二输入模块，四输入的模块的输出可以分为两组，一组最大次大，另一组最小次小。实际上还是按照刚才的拓扑结构，将二输入换成四输入即可：
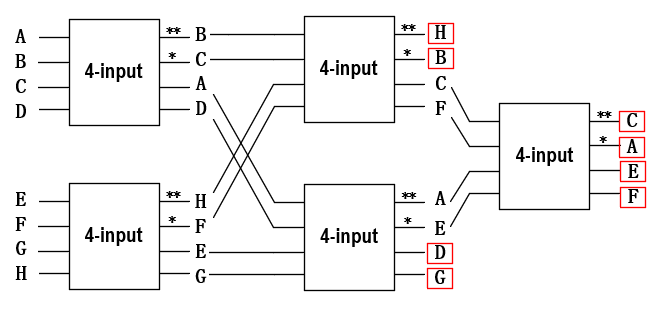
还是按照之前的思路，首先8个输入分为两组，每组之间排序。之后按照刚才的逻辑，上一组的最大次大和下一组的最大次大送入四输入排序模块，就可以确定出8个数中的最大和次大。这里可能有人会有疑问。假设如图中所示，第一层出来以后上面的模块输出最大次大是B和C,下面模块输出最大和次大是H和F,这四个数中一定会产生8个数中的最大和次大值么？答案是肯定的，因为对于A和D而言，B和C一定比他们大，所以没权利坐上8个里的第一第二的宝座，同理E和G也是。所以最大和次大值一定在B,C,H,F中产生。同理，最小和次小就会在A,D,H,F中产生。所以第二级结束后8个数中的最大，次大，最小， 次小就确定了。剩下四个再来一级比较一下就排序完成了。
所以按照这种方法，8个数进行排序需要的二输入比较器个数就是5*5=25个。
经评论区@SpiritzQAQ君的提示，确实后面三个4输入模块没必要取完整，实际上可以只用4输入模块中的后三个二输入比较器，因为这几级的输入大小关系已经确定，更改后的拓扑图如下：
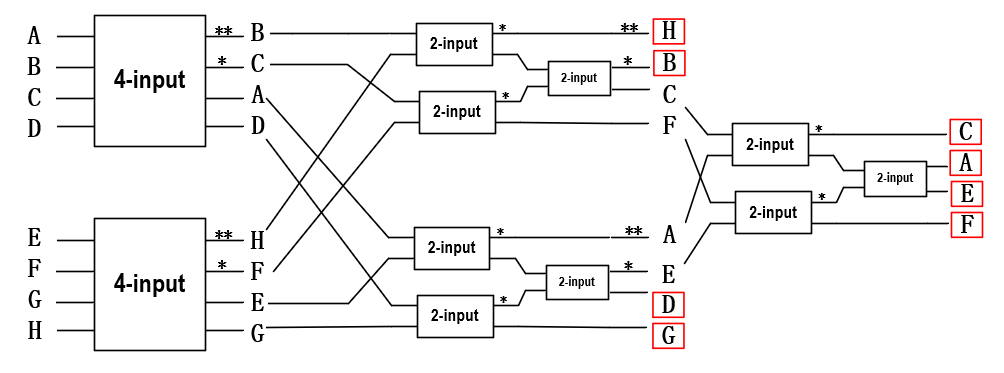
3. 延伸思考
事实上，上面的硬件实现方式就是归并排序的展开实现，归并排序算法如下：
参考：https://www.cnblogs.com/onepixel/articles/7674659.html
归并排序是建立在归并操作上的一种有效的排序算法。该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为2-路归并。
算法描述：
- 把长度为n的输入序列分成两个长度为n/2的子序列；
- 对这两个子序列分别采用归并排序；
- 将两个排序好的子序列合并成一个最终的排序序列。
https://images2017.cnblogs.com/blog/849589/201710/849589-20171015230557043-37375010.gif
再想一下，这一题最本质的问题其实是：
给定n个数的排序，最少需要的比较次数是多少？
如果从信息论的角度来看，n个数的排序总共有\(A_n^n=n!\)种情况，对应的信息量就是\(log_2(\frac{1}{n!})\)，而一次比较获得的信息量\(log_2(\frac{1}{2})\).所以理论的最少比较次数就是：\(log_2(\frac{1}{n!})/log_2(\frac{1}{2}) = log_2(n!)\)。可以发现当n=4时，理论比较次数为\(log_212\), 向上取整就是5，跟我们的电路中用到的比较器个数相同。但是当n=8时，理论的最少比较次数是\(log_28! =15.3\),也就是需要16次比较。那为什么我们这里用到了25个比较器呢？实际上这是因为题目限制了我们只能使用比较器，而要实现理论最小的比较次数还需要其他逻辑的支持，比如MUX。所以上述19个比较器只是归并排序算法的一种硬件实现方式，但并不一定是比较次数最少的硬件实现方式（考虑使用其他逻辑的话）。
PS: 5个数排序的理论最少排序次数（7）的一种比较逻辑：5个数排序最少比较次数
使用这种方法推导8个数的最少比较次数可以得出最少需要18次，但仍然不是理论最少的。据说理论最少的比较次数并不一定能达到。。。
