Verilog -- 乘法器Booth算法
Verilog -- 乘法器Booth算法
1. 原理
Booth算法的原理其实小学初中就学过,比如下面这道题:
简便计算:\(8754 \times 998 = ?\)
随便抓个娃娃来都知道应该这么算:
\(8754 \times 998 = 8754 \times 1000 - 8754 \times 2\)
我们都知道在十进制里,10的倍数的乘法很容易,就是后面加几个0的事情,而上面这种简便计算都有个特点,就是会有999,1001,997,1002这种数,0和9出现的次数很多,这样就可以通过变为化简变为简单的乘法和加减法。
对于二进制数,这种简便计算的情况往往更多。因为计算机中为了计算方便,往往将数据转换为补码的形式,而补码形式在计算时会扩展符号位,比如有符号数补码5'b10110 = -10,在计算与一个8位数相加时会扩展为8‘b11110110,可以发现,这种数往往会有很多连续的1出现,这跟上面的简便计算的例子非常相似。比如:
这就是booth算法分解乘数的基本原理。
2. 一般化推论
假设A和B是乘数和被乘数,且有:
最后的Val(A)的表达式实际上就是补码A表示的原码。
3. 实际算法
上面的公式推导了booth乘法对乘数的分解原理,实际上在编码时只需要公式3,可以做如下的编码表:
| \(a_i\) | \(a_{i-1}\) | \(a_{i-1}-a_i\) | 操作 |
|---|---|---|---|
| 0 | 0 | 0 | 无 |
| 1 | 0 | -1 | 减B |
| 1 | 1 | 0 | 无 |
| 0 | 1 | 1 | 加B |
举个栗子:
\(N=7, B = 22 = (0010110)_2,A=-34=-(0100010)_2\)
首先计算-B的补码(算法中要用到):\(\overline{-B} = (1101010)_2\)
以及A的补码:\(\overline{A} = (1011110)_2\)
硬件计算过程如下:
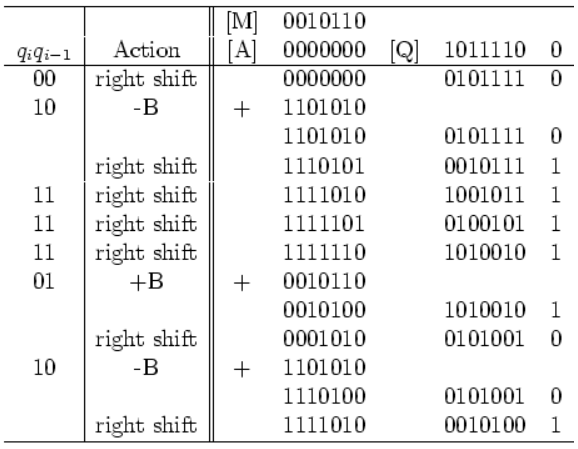
首先初始化p空间:\(p=2N+1\).[A]和[Q]是两个寄存器。其中[Q]是N+1位的。
- 首先将乘数A的补码放到[Q]的高N位上,Q的最低为默认为0.(这步是为了\(i=0\)时,让\(a_{-1}=0\)。
- 在Q中检查\(a_{i-1}-a_i\),得00,查表得无操作,直接将[A]和[Q]合起来右移(算数移位)
- 在Q中检查\(a_{i-1}-a_i\),得10,查表得减B,相当于加-B的补码,在[A]寄存器中加上-B的补码,之后右移
- ...
最后的结果11110100010100就是结果的补码,也就是:
\(B\times A = \overline{11110100010100} = (10001011101100)_原 = -748_{10}\)
算法跟公式的匹配:
实际上,对于公式中的每一项\((a_{i-1}-a_i)\times B\times 2^i\)都对应实际算法中的每一步。\((a_{i-1}-a_i)\)决定了B的系数,右移操作因为作用在[A][Q]寄存器上,所以实际上是相当于将积右移,等价于B左移,所以这一步对应\(\times 2^i\)操作。加减B的操作都作用在[A]寄存器上,保证了\(\times 2^i\)后的B能够作用在正确的位上。
4. Verilog代码
这里只放一种状态机实现的时序逻辑电路,计算过程基本跟上面的算法一样。
参考了
的代码,提供者fanhu, fh_w@outlook.com
`timescale 1ns/1ps
module booth_fsm
# (parameter DATAWIDTH = 8)
(
input clk,
input rstn,
input en,
input [DATAWIDTH-1:0] multiplier,
input [DATAWIDTH-1:0] multiplicand,
output reg done,
output reg [2*DATAWIDTH-1:0] product
);
parameter IDLE = 2'b00,
ADD = 2'b01,
SHIFT = 2'b11,
OUTPUT = 2'b10;
reg [1:0] current_state, next_state; // state registers.
reg [2*DATAWIDTH+1:0] a_reg,s_reg,p_reg,sum_reg; // computational values.
reg [DATAWIDTH-1:0] iter_cnt; // iteration count for determining when done.
wire [DATAWIDTH:0] multiplier_neg; // negative value of multiplier
always @(posedge clk or negedge rstn)
if (!rstn) current_state = IDLE;
else current_state <= next_state;
// state transform
always @(*) begin
next_state = 2'bx;
case (current_state)
IDLE : if (en) next_state = ADD;
else next_state = IDLE;
ADD : next_state = SHIFT;
SHIFT : if (iter_cnt==DATAWIDTH) next_state = OUTPUT;
else next_state = ADD;
OUTPUT: next_state = IDLE;
endcase
end
// negative value of multiplier.
assign multiplier_neg = -{multiplier[DATAWIDTH-1],multiplier};
// algorithm implemenation details.
always @(posedge clk or negedge rstn) begin
if (!rstn) begin
{a_reg,s_reg,p_reg,iter_cnt,done,sum_reg,product} <= 0;
end else begin
case (current_state)
IDLE : begin
a_reg <= {multiplier[DATAWIDTH-1],multiplier,{(DATAWIDTH+1){1'b0}}};
s_reg <= {multiplier_neg,{(DATAWIDTH+1){1'b0}}};
p_reg <= {{(DATAWIDTH+1){1'b0}},multiplicand,1'b0};
iter_cnt <= 0;
done <= 1'b0;
end
ADD : begin
case (p_reg[1:0])
2'b01 : sum_reg <= p_reg+a_reg; // + multiplier
2'b10 : sum_reg <= p_reg+s_reg; // - multiplier
2'b00,2'b11 : sum_reg <= p_reg; // nop
endcase
iter_cnt <= iter_cnt + 1;
end
SHIFT : begin
p_reg <= {sum_reg[2*DATAWIDTH+1],sum_reg[2*DATAWIDTH+1:1]}; // right shift
end
OUTPUT : begin
product <= p_reg[2*DATAWIDTH:1];
done <= 1'b1;
end
endcase
end
end
endmodule
testbench:
`timescale 1ns/1ps
// Basic exhaustive self checking test bench.
`define TEST_WIDTH 10
module booth_fsm_tb;
reg clk;
reg rstn;
reg en;
integer multiplier1;
integer multiplicand1;
reg [`TEST_WIDTH-1:0] multiplier;
reg [`TEST_WIDTH-1:0] multiplicand;
wire done;
//输入 :要定义有符号和符号,输出:无要求
wire signed [2*`TEST_WIDTH-1:0] product;
wire signed [`TEST_WIDTH-1:0] m1_in;
wire signed [`TEST_WIDTH-1:0] m2_in;
reg signed [2*`TEST_WIDTH-1:0] product_ref;
reg [2*`TEST_WIDTH-1:0] product_ref_u;
assign m1_in = multiplier[`TEST_WIDTH-1:0];
assign m2_in = multiplicand[`TEST_WIDTH-1:0];
booth_fsm #(.DATAWIDTH(`TEST_WIDTH)) booth
(
.clk(clk),
.rstn(rstn),
.en(en),
.multiplier(multiplier),
.multiplicand(multiplicand),
.done (done),
.product(product)
);
always #1 clk = ~clk;
integer num_good;
integer i;
initial begin
clk = 1;
en = 0;
rstn = 1;
#2 rstn = 0; #2 rstn = 1;
num_good = 0;
multiplier=0;
multiplicand=0;
#8;
for(i=0;i<4;i=i+1) begin
en = 1;
multiplier=10'b10000_00000+i;
multiplicand=10'b00000_00010+i;
wait (done == 0);
wait (done == 1);
product_ref=m1_in*m2_in;
product_ref_u=m1_in*m2_in;
if (product_ref !== product)
$display("multiplier = %d multiplicand = %d proudct =%d",m1_in,m2_in,product);
@(posedge clk);
end
$display("sim done. num good = %d",num_good);
end
initial begin
$fsdbDumpvars();
$fsdbDumpMDA();
$dumpvars();
#1000 $finish;
end
endmodule
仿真波形:




 浙公网安备 33010602011771号
浙公网安备 33010602011771号