专用集成电路 -- CMOS组合逻辑设计
专用集成电路 -- CMOS组合逻辑设计
《数字集成电路--电路、系统与设计》第二版 复习笔记
1. 静态互补CMOS
实际上就是静态CMOS反相器扩展为具有多个输入。更反相器一样具有良好的稳定性,性能和功耗。
- 静态的概念:每一时刻每个门的输出通过低阻抗路径连到VDD或VSS上。任何时候输出即为布尔函数值。
- 动态电路通常依赖把信号暂存在高阻抗节点的电容上。
1.1 阈值损失

互补结构PUN(pull up network)+PDN(pull down network)可以解决。
1.2 两输入与非门实例
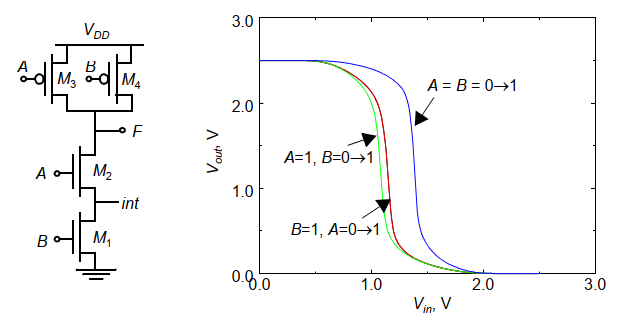
与非门的VTC曲线与输入有关,从下图可以发现,A=B=0时,PUN全部导通,对应强上拉,而当A或B中有不导通的时候,PUN中只有一个导通,相当于驱动能力下降(在反相器中提到P管驱动能力下降导致VTC左移,VM上漂),因此VTC左移到红色和绿色线。
而红绿两线的主要区别在于NMOS的内部节点int上,由于体效应的缘故会使得M1和M2在分别导通时阈值电压不同,VTC曲线会有微小的差异。
虽然互补CMOS是实现逻辑门比较简单的方式,但是随着扇入增加,会带来两个问题:
- 实现一个N扇入的门需要2N个器件,会增大实现面积。
- 互补CMOS的传播延时随着扇入增大迅速增大(无负载本征延时在最坏时与扇入成二次函数关系)
1.3 延时与扇入的关系
例如对于一个四输入与非门:

- 在最坏情况下,PUN只导通一条通路,此时从低到高的延时\(t_{pLH}\)最大,当增大扇入数,PUN的器件随着扇入线性增加,电容也线性增加,但最坏情况PUN的等效电阻不变,因此\(t_{pLH}\)随着N的增加呈线性增加。
- 而对于PDN,串联会使得门进一步变慢。在PDN中分布RC网络带来的延时与串联链元件数呈平方关系。因此\(t_{pHL}\)是输入的二次函数:\(t_{pHL}=a_1FI+a_2FI^2+a_3FO\),其中FI=扇入,FO = 扇出。
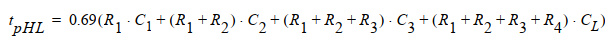
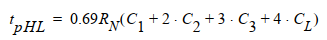
下图是NAND门的本征传播延时与扇入的关系曲线:
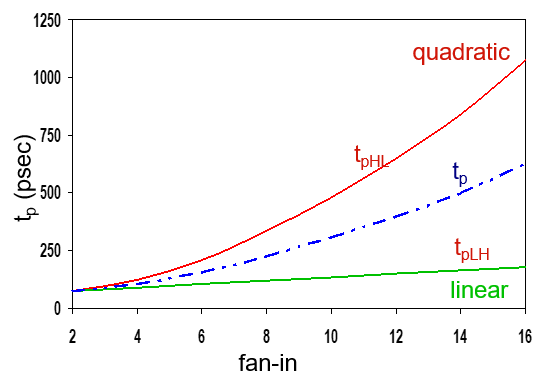
1.4 解决大扇入的方法
- 增大晶体管尺寸。可以减少串联电阻。
- 局限:会增加寄生电容。只有当负载以扇出电容为主时有用,否则只会增加"自载效应"。
- 逐级加大尺寸。因为从公式中可以看到M1-M4的电阻出现次数依次递增,所以因该让他们的电阻值依次递减才能得到最优解。
- 局限: 在实际版图中不易实现。
- 重新安排输入。由于输入信号不都在同时间到达,因此可以把关键信号放到靠近输出端的晶体管上以提高速度。(关键信号:在所有输入中最后到达稳定值的信号)
- 重组逻辑结构。比如,将6输入OR门变为两个三输入NOR门加上一个二输入与非门。原理是减小了扇入。
问题:为什么把关键信号放到靠近输出端的晶体管上可以提高速度?
其实就是一个放电顺序的问题:
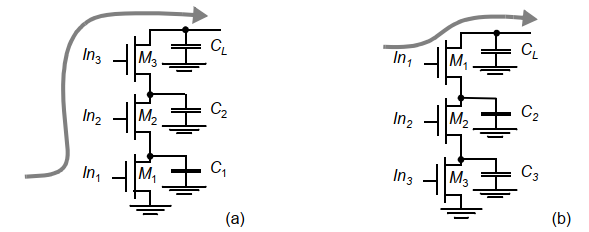
上图中,如果M1是最后才导通的那个,则直到M1导通前CL和C2都无法放电。而把M1放到最上面以后,C2和C1就可以先放电,节省了时间。
2. 组合逻辑性能优化
跟反相器链的性能优化类似,前面已经知道对于一个CL负载,驱动其的最优每级扇出\(f = (C_L/C_{in})^{1/N}\),并且最优扇出保持在4左右。
那么对于任何组合逻辑而言,又该如何呢?
这里将原来的反相器链(上面的公式)改写为(下面的公式):
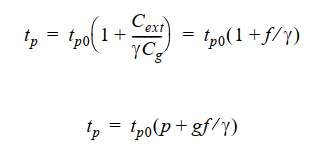
其中,\(f\)仍然是等效扇出,此外,在这里也称为电气努力(electrical effort)。\(p\)代表复合门与简单反相器的本征延时比,与门的拓扑结构和版图样式有关。下面是一些\(p\)的典型值:
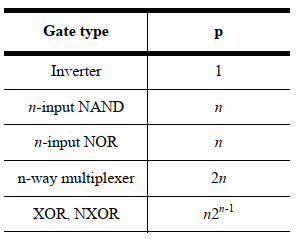
2.1 逻辑努力,门努力
系数\(g\)称为逻辑努力(logical effort)。可以有下面几种表达方式:
- 他表示对于给定负载,复合门必须比反相器更努力工作(电流)才能得到类似响应。
- 当逻辑门的每个输入的输入电容跟一个反相器相同,在产生输出电流方面比这个反相器差多少。
- 当逻辑门的输出电流与一个标准反相器相同时,它的输入电容是反相器的多少倍。
下面是一些常用门的逻辑努力:
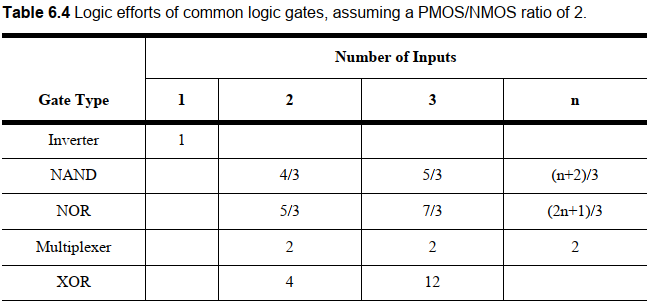
下面这个例子可以直观地理解逻辑努力的含义:

对于一个最小尺寸反相器,其P管尺寸是N管2倍。因此输出电容是N管电容(\(C_{unit}\))的3倍。为了确定NAND和NOR的尺寸,如果要保证输出电流相同,也就是等效电阻和标准反相器相同。这就提出了要求:PUN等效尺寸=2,PDN等效尺寸=1.对于并联来说,等效电阻=最坏情况也就是只有一个导通的电阻,所以PMOS尺寸仍为2;对于串联,尺寸变大一倍,等效电阻变为一半。
由此可见,NAND尺寸变换后等效的输入电容变为\(4C_{unit}\)。也就是最小反相器的4/3.也就是逻辑努力为4/3。同理,NOR的逻辑努力为5/3。
一个逻辑门的延时可以分为两部分,努力延时和本征延时:

上图中,直线斜率就是逻辑努力,y轴交点就是本征延时。此外,把 \(h=gf\)称为门努力(gate effort)。
2.2 组合逻辑链最小延迟计算
组合逻辑链的延时可以表示为:

- 分支努力(branching effort): \(b = \frac{C_{onpath}+ C_{offpath}}{C_{onpath}}\).分支努力其实就是表示在该路径上本级的输出负载与流入下一级的有效负载的比值。
- 路径分支努力(path branching effort): \(B = \prod_1^N b_i\)
- 路径电气努力: \(F = \prod_1^N \frac{f_i}{b_i} = \frac{\prod f_i}{B}\)
- 总路径努力: \(H = \prod_1^N h_i = \prod_1^N g_if_i=GFB\)
因此,与反相器链类似,使得延时最小的门努力为:
所以最小延时为:

3. CMOS逻辑门中的功耗
复合CMOS逻辑门的功耗和反相器中讨论的类似,也是与以下几个因素有关:
- 器件尺寸(电容)
- 输入和输出上升下降时间(决定短路功耗)
- 器件阈值和温度(影响漏电功耗)
- 开关活动性(开关功耗)
当门比较复杂的时候,受影响最大的是开关活动性\(\alpha_{0->1}\),可以分为两部分:
- 只与逻辑电路拓扑结构有关的静态部分
- 由时序特性引起的动态部分(虚假尖峰信号或毛刺Glitch)
3.1 开关活动性的静态部分
静态部分与所实现的逻辑功能(真值表)密切相关。例如:对于一个N输入的NOR门,假设\(p_a\)和\(p_b\)表示输入A和B分别为1的概率,且输入不相关(这个假设很难成立)。则输出为1的概率为:\(p_1 = (1-p_a)(1-p_b)\),这个表达式是根据真值表推导出的。
则由0到1的翻转概率为:
下图展示了这种关系:
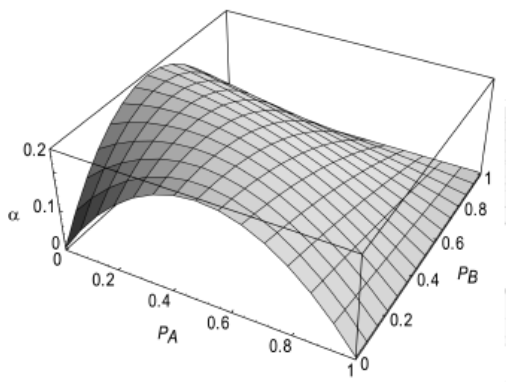
上面算法的局限性:
- 不适用于在时序电路中出现的具有反馈的电路。
- 其假设每个门的输入信号概率不相关是很少见的。
3.2 开关活动性的动态虚假翻转
从一个逻辑块到另一个逻辑块的非零传播延时可能会引起毛刺或动态故障(dynamic hazard) 的虚假翻转。在一个时钟周期内节点在稳定到正确电平之前可以多次翻转。下面这个例子可以解释这种虚假翻转:

上图是一个NAND门链在输入同时从0->1时的响应。开始时输入为0,所以说有节点的输出均为1。当出现输入的翻转时,理论上最终的输出奇数位都是0,偶数为都是1。但是从图中可见out1在一定延时后降为0(红线),由于存在这个延时,导致out2的输出在out1稳定之前(相当于NAND输入11),会有像0翻转的趋势,直到out1基本稳定下来(趋于0)时,out2才又往1翻转。导致了图中的绿色线。
虚假翻转的危害:
- 偶数位上的这些毛刺造成了逻辑功能外的额外功耗(因为从逻辑分析来看这些位不应该变化)。虽然这个例子中毛刺并不是轨到轨的变化,但是却可能构成很大的功耗。
- 对于一些加法器,乘法器,会出现比较长的逻辑门链,毛刺功耗就很容易成为主要部分。
3.3 降低组合逻辑的开关活动性
-
逻辑重组:
- 下面是4输入与门的两种实现,链式结构和树形结构。如果不考虑上面提到的虚假翻转毛刺,从开关活动性来看链式的结构具有更低的静态活动性。
- 但是实际上也要考虑时序特性,考虑毛刺功耗,因为树形结构没有任何毛刺活动(每级信号延时都相等)。

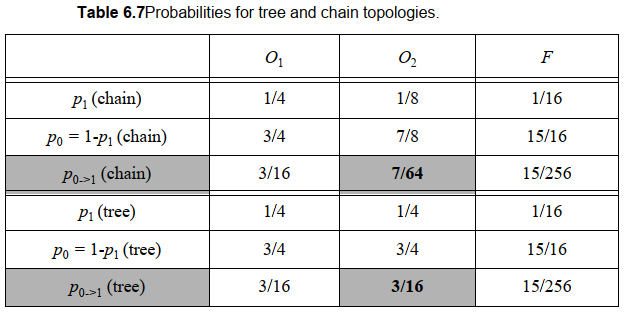
-
输入排序:
- 将具有较高翻转率的信号放到靠近输出端的输入端上。
- 可以看下面的例子,首先两个电路输出的翻转率是相同的,主要看中间节点。对于第一种,活动性等于\((1 - 0.5 * 0.2) (0.5* 0.2) = 0.09\).而对于第二种,活动性等于\((1 – 0.2 * 0.1) (0.2 * 0.1)= 0.0196\)
-

-
分时复用资源:
- 分时复用某个硬件资源(逻辑单元或总线)来完成多个功能。
- 通常可以减小面积,但不是总能降低开关活动性。例如下面的例子:电容减少为一个,但是可能需要倍频来实现数据的传送,所以对应的开关等效电容是一样的。

- 但是对于传递的数据有一些特性时,分时复用可能收效不高,比如A总是1,B总是0。并行传输时的切换非常少,而分时复用则会有较大翻转。
-
通过均衡信号路径减少毛刺: 毛刺主要是电路中路径长度失陪引起的。因此要解决路径中延时长度不同的问题,可以使用树型结构替换链式结构。
4. 有比逻辑
4.1 伪NMOS
- 有比的概念:输出电平和功能取决于NMOS和PMOS的尺寸比。不同于无比逻辑,无比逻辑高低电平与尺寸无关。
- 目的:有比逻辑的目的是减少晶体管数。从2N降低为N+1.
- 思路:将PUN替换为一个无条件负载器件。通常为一个栅极接地的PMOS负载(伪NMOS门)。
- 缺陷:
- 会降低稳定性和额外功耗。
- 额定低电压不是0,因为存在PDN和伪NMOS的通路。这降低了噪声容限,并且引起了静态功耗。
例子:伪NMOS反相器。
缩小PMOS器件的尺寸可以得到不同的电压传输曲线:
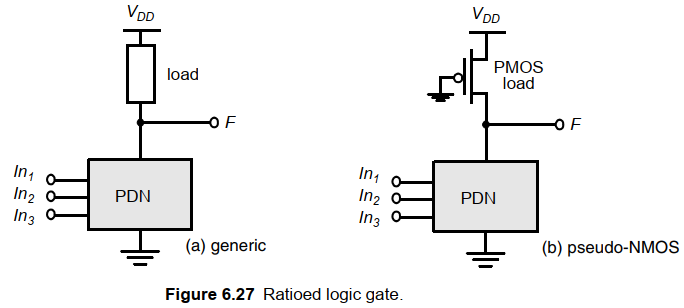

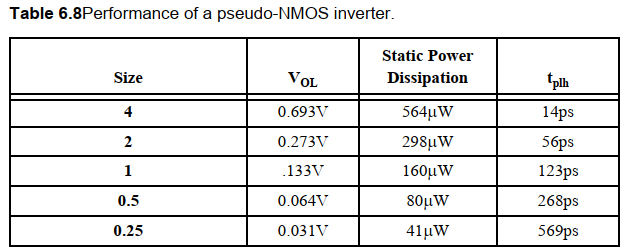
虽然静态功耗限制了伪NMOS的应用,但是当面积是最重要的因素时,伪NMOS还是可以使用的,因此还是可以看到伪NMOS有时应用在大扇入的电路中。
4.2 差分串联电压开关逻辑(DCVSL)
- 目的:完全消除静态电流并提供轨到轨的电压摆幅的有比逻辑。
- 原理:差分逻辑和正反馈。
- 差分门要求每个输入都具有互补形式,同时也产生互补输出。
- 反馈机制保证不需要负载时将其关断。
例子:XOR-XNOR门
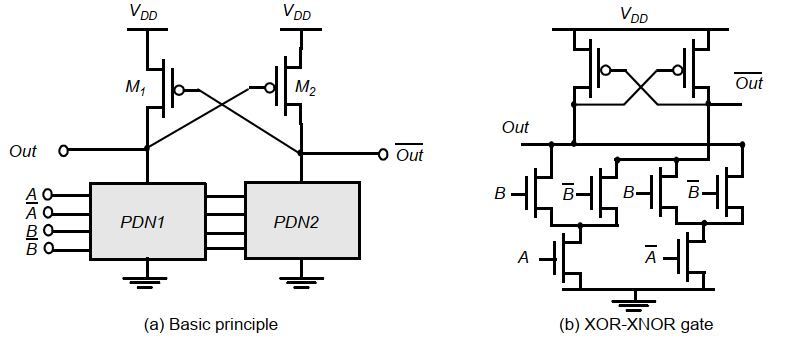
上图中,下拉网络PDN1和2是互斥的,同一时间两只只会有一个导通。
假设最初out为高,out非为低。当PDN1导通时,out下拉。但是PDN1必须足够强劲使得out低于VDD-|VTP|,才能使得M2导通,out非变为VDD,最终将M1关断。
- 优势:
- 消除静态电流,提供轨到轨输出
- 同时产生了输出和其反信号,节省了额外的反相器,避免使用反相器引起的时差问题。这实际上受益于差分逻辑。
- 缺陷:
- 在翻转期间PMOS和PDN会同时导通一段时间,产生短路通路,造成渡越电流。(不同于静态电流,静态电流在PDN导通时一直存在)
- 在实际布线时导线数量加倍,使得电路复杂
- 动态功耗较高
4.3 传输管逻辑
- 目的:减少晶体管数
- 原理:输入驱动栅极和源漏端来减少逻辑需要的晶体管数。只允许驱动栅极的CMOS不同。
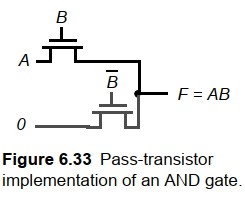
- 缺陷:存在阈值损失。并且由于体效应这种情况更加严重。如下图:
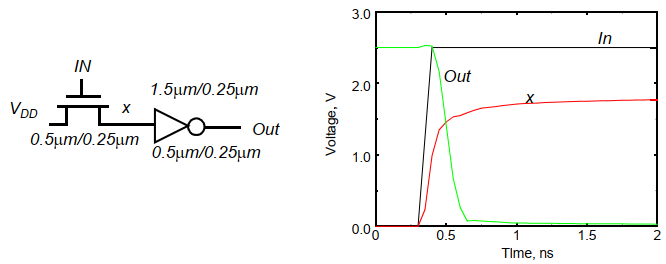
此外,应该避免传输管驱动另一个栅极,这样会导致阈值损失传递:

传输管的VTC与CMOS反相器不同,下图是一个而输入AND传输管的VTC:

可见一个传输门是不能使信号再生的。经过多级后会衰减,可以通过插入反相器来弥补。
4.3.1 差分传输管逻辑CPL
高性能设计中通常使用差分传输管逻辑,称为CPL或DPL.
- CPL属于静态门,输出节点通过低阻路径连到VDD或地。
- 具有模块化特点,门单元库设计简单。
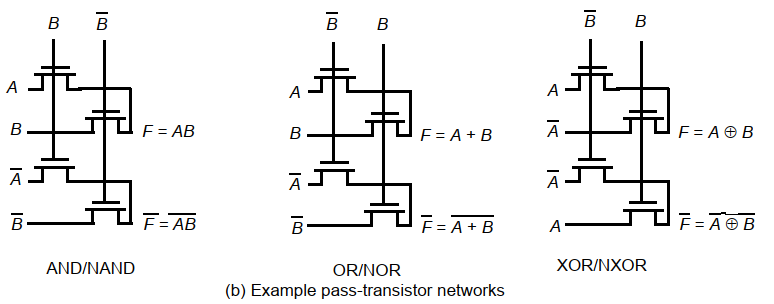
4.3.2 解决阈值损失和静态功耗
问题:由于传输管在高电平无法充电到VDD,少了一个VT,所以在驱动后级的反相器时反相器会有静态功耗。
a. 电平恢复器
一种简单的方法是使用一个PMOS连到反馈环路中:
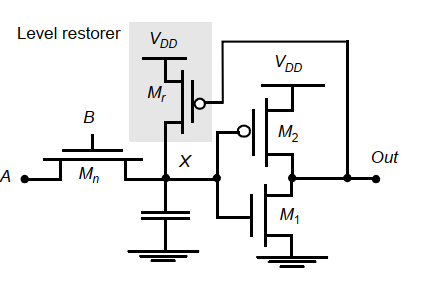
优势:通过上拉的PMOS将高电平充到VDD,消除了后级反相器的静态功耗,传输管和恢复器中也没有静态电流路径。
缺陷:
- 是有比逻辑,增加了复杂性。在节点从高到低的过程中,传输管试图拉低节点,而电平恢复器却要上拉到高,因此传输管的下拉能力必须大于恢复器的上拉能力。这就要求仔细设计各个管的尺寸。
- 电平恢复器对器件切换速度有影响。增加恢复器增加了内部节点X的电容,减慢了门的速度。
b. 多阈值晶体管
使用0阈值的NMOS传输管可以消除大部分阈值损失。所有非传输管都用高阈值器件实现。
缺陷:
- 需要对器件的注入准确控制才能达到0阈值,并且由于体效应,难以真的达到全摆幅
- 用零阈值对功耗有不利影响。这是因为即使器件关断,也会有亚阈值电流流过传输管,如下图:
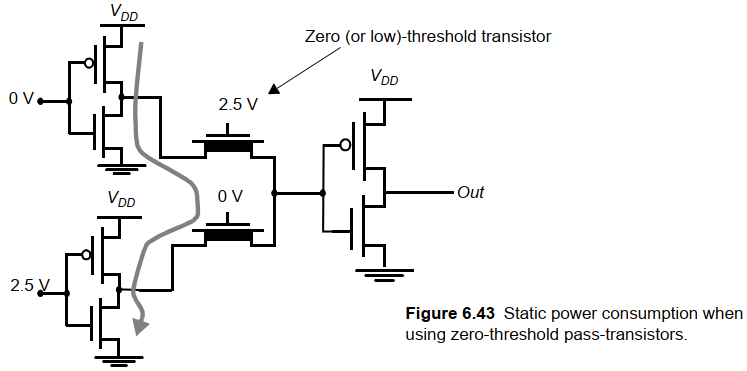
c.传输门逻辑
最广泛采用的是传输门逻辑,利用N和PMOS的互补特性。
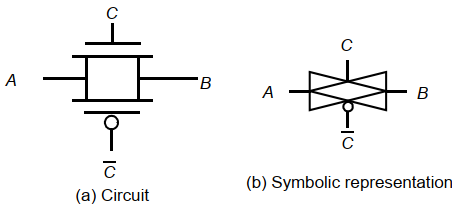
两个管子并联,控制信号相反,任何时候两者都导通。通常消耗更少的管子。例如实现下面的逻辑:

采用CMOS逻辑需要8管,而传输门逻辑只需要6管。(不包括反向输入信号的生成)

4.4 传输门的性能
传输门的高到低和低到高等效电阻基本上可以认为是定值,下图是传输门从低到高的翻转的等效电阻:
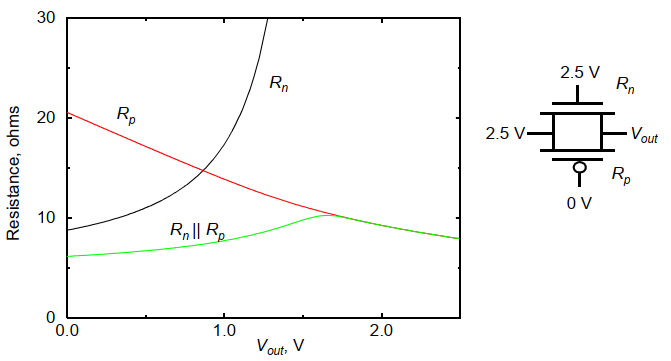
传输门链:
对于传输门链可以使用一阶近似将其等效为电容电阻网络:
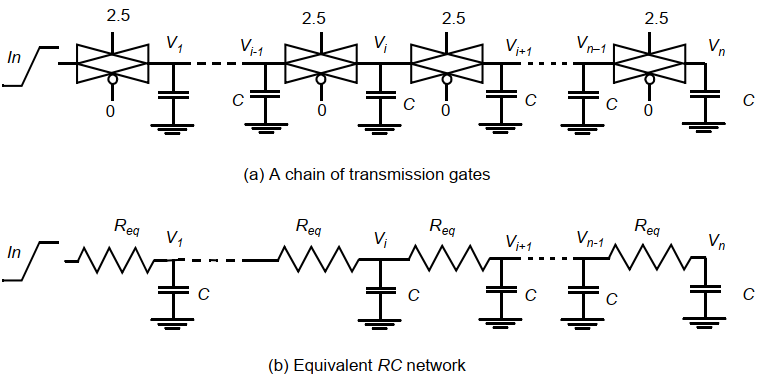
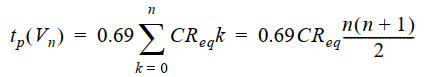
可见传输门延时正比于\(n^2\),因此不能采用过长的传输门链。如果要使用,建议是在传输门链中每隔几个(3~4)传输门插入一个Buffer。
5. 动态CMOS逻辑
在PUN和PDN上下插入CLK控制的管子。主要有两个阶段:预充电和求值。由CLK决定。
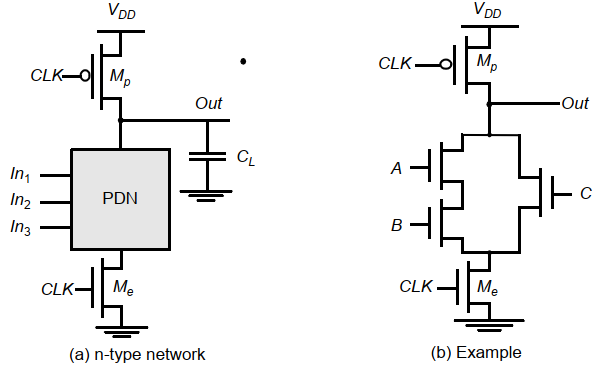
预充电:
CLK=0时输出节点Out被PMOS管预充电至VDD。此期间NMOS求值管关断,所以下拉不工作。求值管消除了预充电期间的任何静态功耗。
求值:
CLK=1时,预充电管关断,输出根据下拉拓扑结构有条件地放电。
优点:
- 逻辑功能只有下拉网络实现,晶体管数少,为N+2个
- 是无比逻辑,功能与尺寸无关。
- 只有动态功耗。理想情况下不存在VDD到GND的静态电流路径。但总功耗还是可能明显高于静态逻辑
- 有较快的开关速度。因为减少了晶体管数,每个扇入只连接到一个负载晶体管,降低了负载电容。相当于降低逻辑努力。另外,动态门没有短路电流。
当然也可以用P型动态门,也就是预充电通过下拉的NMOS实现,但这种的缺点是比n型动态门慢。因为PMOS的驱动电流小。
动态逻辑的噪声容限是极不对称的,比如一个四输入NAND门:
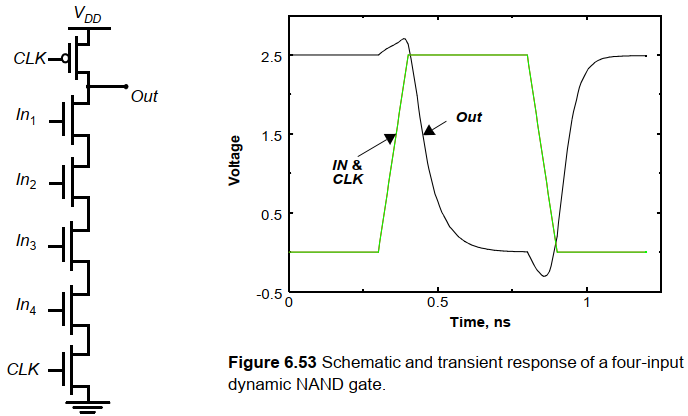
下表是其各项性能参数:

假设输入连在一起,则这个门的开关阈值VM=VTN,高电平噪声容限将有VDD-VTN这么多。
此外,其低到高的传播延时为0,因为预充电后输出总是高电平,对于低电平的输入没有任何变化发生。
实际上,该门的开关阈值与时钟周期有关,下图是不同glitch下该门的响应。可以发现,对于较大的输入翻转,门变化较快。而输出电压下降的幅度实际上还与周期有关,如果求值时间很短,那么噪声电压比如很大才能破坏信号。
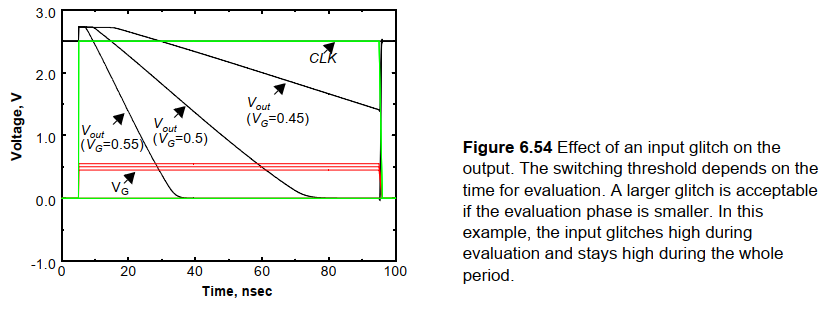
缺陷:
- 动态逻辑的时钟功耗可以很大
- 当增加抗漏电器件时可能会有短路功耗
- 由于周期性的预充和放电,动态逻辑会有较高的开关活动性。
5.1 动态设计的信号完整性
a. 电荷泄露
预充电到高后,电容上将保持高电平,但总是会有泄露电流导致电荷漏掉。如下图:

可见存储在CL上的电荷将通过漏电左图的几个漏电渠道漏掉,因此动态电路有一个最低的频率要求,一般为几KHZ。
解决方法:
电荷泄露的解决通常通过增加伪NMOS上拉以及反馈来补偿:
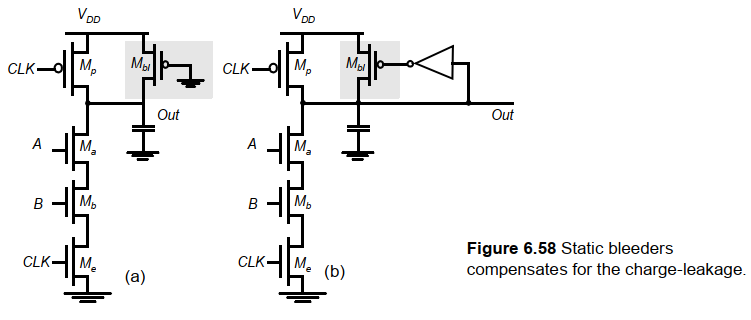
通过反馈来控制上拉管可以降低静态功耗。通常泄露器的尺寸比较小,以保证下拉网络可以下拉。
b. 电荷分享
下图展示了电荷分享。在求值期间,假设B=0,A置高后Ma导通,CL上的电容会在CL和Ca之间重新分配,导致输出电平的降低。
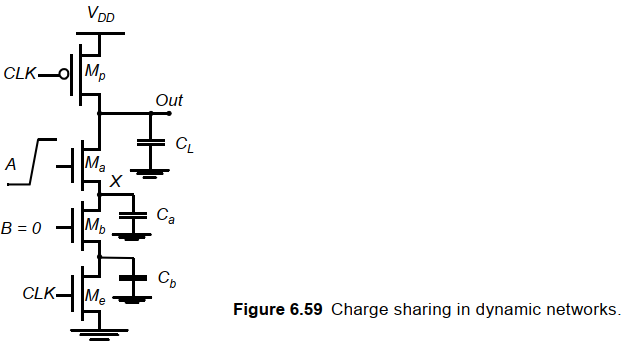
解决方法:
通过对关键的内部节点预充电:

c. 电容耦合
输出节点较高的阻抗使得电路对串扰很敏感。
- 当有导线在动态节点上或邻近时,会产生耦合电容破坏浮空节点。
- 回栅耦合(backgate),输出耦合至输入。
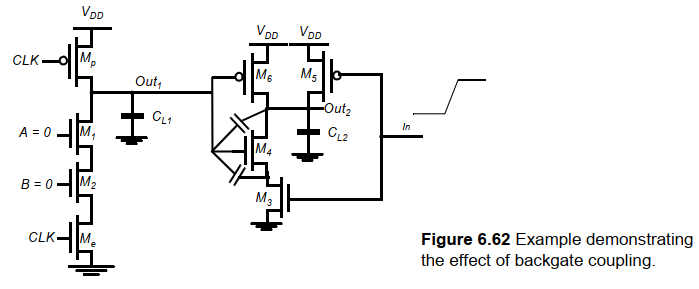
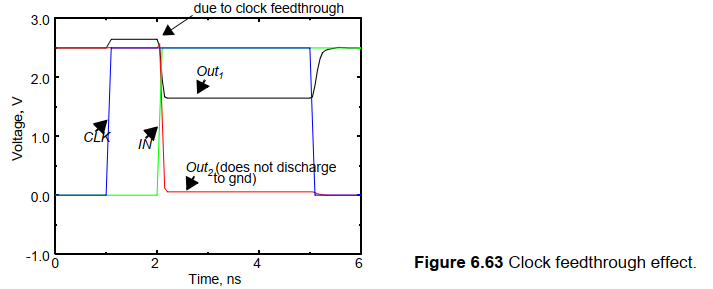
d. 时钟馈通
电容耦合的特殊情况。在预充器件的时钟输入和动态节点之间的电容耦合引起。耦合电容由预充器件的栅漏电容组成。
其次,快速上升和下降的时钟边沿会耦合到信号节点上。例如上图中显示的那样。
5.2 动态门的串联
动态门的串联会遇到延时的问题,例如下面的电路:
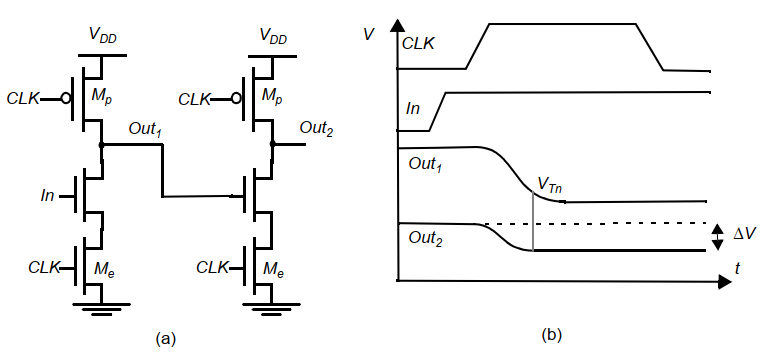
多米诺逻辑:
动态逻辑后加一个反相器,再级联其他多米诺逻辑。反相器可以保证动态逻辑再预充电后输出为0,避免1->0的翻转。

np-CMOS:
使用n型动态逻辑和p型动态逻辑串联,避免引入额外静态反相器。
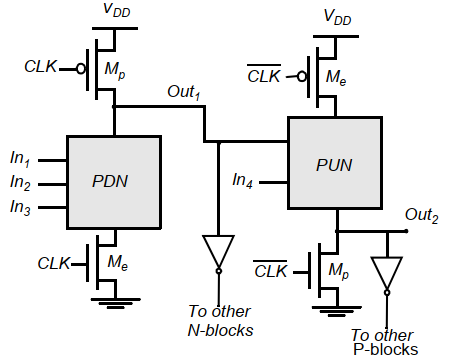
n型预充电为高,因此不会导致下一级的PUN提前导通。



