Verilog -- 无符号整数除法器(一)
参考: https://blog.csdn.net/rill_zhen/article/details/7961937
https://www.cnblogs.com/moranhuishou0315/p/11344725.html
Verilog -- 无符号整数除法器(一)
在不使用除法的前提下,如何设计一个快速高效的除法器?
在Verilog HDL语言中虽然有除的运算指令,但是除运算符中的除数必须是2的幂,因此无法实现除数为任意整数的除法,很大程度上限制了它的使用领域。并且多数综合工具对于除运算指令不能综合出令人满意的结果,有些甚至不能给予综合。即使可以综合,也需要比较多的资源。
最简单的方法就是减法实现除法器(比如十进制中的a/b,可先比较a与b的大小,如果a>b,则商加1,a<=a-b,再进行比较大小,直到a<b,商不变,余数为a)。但这种方式通常速度比较慢,实际上更快速的方法是模拟手算除法的过程:
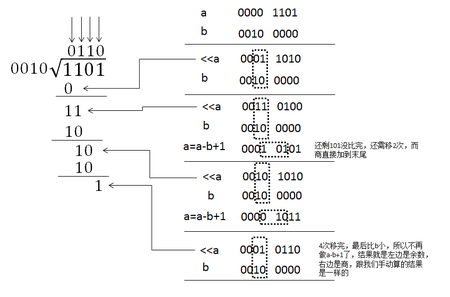
实际上上图演示的是二进制除法运算,跟十进制的没多大区别,只不过十进制的除法商的每一位都有0-9十种可能,因此如果采用十进制来编写除法器需要采用二分法逐个判断商的每一位上的数字,而二进制因为只有两种可能所以不需要那么麻烦(但其实两者的本质是一样的,算法的时间复杂度相同)
流程图:
graph LR
id0(32位整数a除以b)-->id1(a的高位扩展32位)
id0(32位整数a除以b)-->id2(b的低位扩展32位)
id1 --> id3(a左移一位)
id2 --> id4{a>=b?}
id3 --> id4
id4 -- 是 --> id5(a = a-b+1)
id5 -->id6{移位次数<32}
id4 --否-->id6
id6 --是--> id3
id6 --否--> id7(输出a)
最后输出的商=a高32位,余数=a低32位
module int_div
(
input[31:0] a,
input[31:0] b,
output reg [31:0] yshang,
output reg [31:0] yyushu
);
reg[31:0] tempa;
reg[31:0] tempb;
reg[63:0] temp_a;
reg[63:0] temp_b;
integer i;
always @(a or b)
begin
tempa <= a;
tempb <= b;
end
always @(tempa or tempb)
begin
temp_a = {32'h00000000,tempa};
temp_b = {tempb,32'h00000000};
for(i = 0;i < 32;i = i + 1)
begin
temp_a = {temp_a[62:0],1'b0};
if(temp_a[63:32] >= tempb)
temp_a = temp_a - temp_b + 1'b1;
else
temp_a = temp_a;
end
yshang <= temp_a[31:0];
yyushu <= temp_a[63:32];
end
endmodule
testbench:
`timescale 1ns/1ns
module int_div_tb;
reg [31:0] a;
reg [31:0] b;
wire [31:0] yshang;
wire [31:0] yyushu;
initial
begin
#10 a = $random()%10000;
b = $random()%1000;
#100 a = $random()%1000;
b = $random()%100;
#100 a = $random()%100;
b = $random()%10;
#1000;
end
int_div div
(
.a (a),
.b (b),
.yshang (yshang),
.yyushu (yyushu)
);
initial begin
$fsdbDumpvars();
$dumpvars();
#1000 $finish;
end
endmodule
波形:

上面这种写法其实不是一个好的写法,因为纯组合逻辑实现可能会有较大的延时,并且可能会综合出锁存器,因此将其设计为时序逻辑是更好的选择,详见下一篇“Verilog -- 任意整数除法器(二)”。



