第九周作业
20182313 2019-2020-1 《数据结构与面向对象程序设计》第九周学习总结
教材学习内容总结
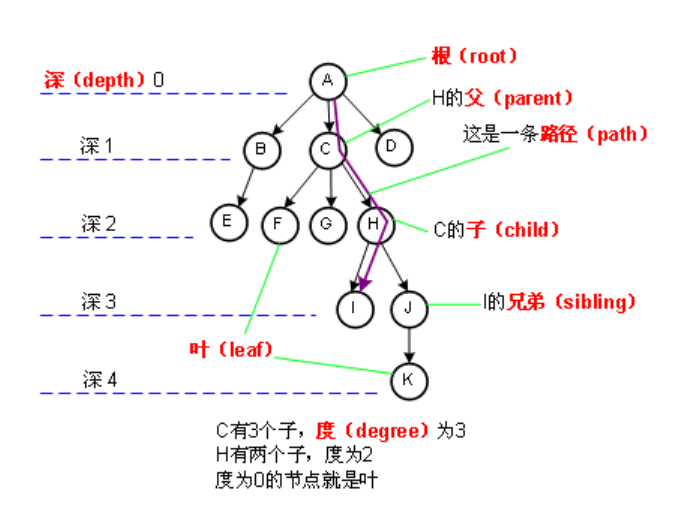
- 树(tree)是一种非线性结构,其中元素被组织成了一个层次结构。
- 树由一个包含结点(node)和边(edge)的集构成。元素被存储在这些结点中,边将一个结点和另一个结点连接起来。
- 每一结点都位于该树层次结构中的某一特定层上。树的根(root)就是那个位于该树顶层的唯一结点。
- 位于树中较低层的结点是上一层结点的孩子( children)。
- 一个结点只有一个双亲,但是一个结点可以有多个孩子。同一双亲的两个结点称为兄弟( sibling)。根结点是树中唯一一个没有双亲的结点。没有任何孩子的结点称为叶子(leaf)。一个至少有一个孩子的非根结点称为一个内部结点( internal node)。
- 树的类比是上下倒置的。
- 根是树结构的进入点。我们可以沿着一条通过该树的路径从双亲到达孩子。
- 假如A在从根开始的路径中位于另一结点B之上,则A就是B 的祖先( ancestor)。根是树中所有结点的最终祖先。沿着起始自某一特定结点的路径可以到达的结点是该结点的子孙( descendant)。
- 结点的层也就是从根结点到该结点的路径长度。通过计算从根到该结点所必须越过的边数目,就可以确定其路径长度( path length)。根是位于层0的。
- 树的高度( height)是指从根到叶子之间最远路径的长度。
![image]()
- 树的遍历
- 先序遍历
即根节点在左右子树之前遍历:先访问根节点再先序遍历左子树再先序遍历右子树退出 - 中序遍历
先中序遍历左子树再访问根节点再中序遍历右子树退出 - 后序遍历
即根节点在左右子树之后遍历:先后序遍历左子树再后序遍历右子树最后访问根节点退出 - 层序遍历
即从根节点开始,访问每一层的所有结点,一次一层
- 树的分类
1.二叉树: 二叉树是有限个节点的集合,这个集合可以是空集,也可以是一个根节点和至多两个子二叉树组成的集合,其中一颗树叫做根的左子树,另一棵叫做根的右子树。简单地说,二叉树是每个节点至多有两个子树的树
- 完全二叉树:完全二叉树是一种特殊的二叉树,满足以下要求:
(1).所有叶子节点都出现在 k 或者 k-1 层,而且从 1 到 k-1 层必须达到最大节点数;
(2).第 k 层可是不是慢的,但是第k层的所有节点必须集中在最左边。简单地说,就是叶子节点都必须在最后一层或者倒数第二层,而且必须在左边。任何一个节点都不能没有左子树却有右子树。 - 满二叉树:如果一棵树的高度为k,且拥有2^k-1个节点,则称之为 满二叉树。就是说,每个节点要么必须有两棵子树,要么没有子树。
- 二叉查找树:它最大的特点就是左孩子小于父节点,右孩子大于父节点,这种特点让二叉查找树从创建到插入元素都能维持排序的属性(主要表现在:中序遍历时元素能准确按照由小到大的顺序排列),有利于之后对树中元素的处理,特别是需要用到搜索时能大大提高搜索效率(低至O(log₂n))
| 操作 | 说明 |
|---|---|
| addElement | 往树中添加一个元素 |
| removeElement | 从树中删除一个元素 |
| removeAllOccurences | 从树中删除所指定元素的任何存在 |
| removeMin | 删除树中的最小元素 |
| removeMax | 删除树中的最大元素 |
| findMin | 返回一个指向树中最小元素的引用 |
| findMax | 返回一个指向树中最大元素的引用 |
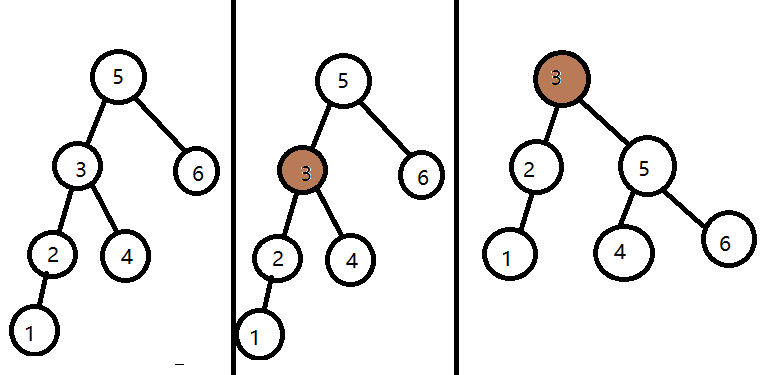
- 平衡二叉查找树
旋转:以右旋为例,其应用于左子树高度过高的非平衡树的平衡化中,步骤为:
使(子)树根的左孩子元素成为新的根元素;
使原根元素成为这个新树根的右孩子元素;
使原树根的左孩子的右孩子,成为原树根的新的左孩子。
![image]()
教材学习中的问题和解决过程
- 问题一:树的高度和深度的区别?
- 问题一解决过程:高度的定义课本给出的是指从根到叶子之间最远路径的长度。还有的说法是从结点x向下到某个叶结点最长简单路径中边的条数,深度是从根节点往下,深度是从根节点开始(其深度为1)自顶向下逐层累加的。总的来说对于整棵树来说,最深的叶结点的深度就是树的深度;树根的高度就是树的高度。这样树的高度和深度是相等的。对于树中相同深度的每个结点来说,它们的高度不一定相同,这取决于每个结点下面的叶结点的深度。
- 问题二:决策树中提到的is-a关系是什么关系?
- 问题二解决过程:是类的父子继承关系,例如类D是另一个类B的子类(类B是类D的父类)。换句话说,通常"D is-a B"(B把D包含在内,或是D被包含在B内)指的是,概念体D物是概念体B物的特殊化,而概念体B物是概念体D物的一般化。举例来说,水果是苹果、橘子、芒果与其他水果的一般化。
- 问题三:ExpressionTreeOp类中的int型变量termType=1的用处是什么?
- 问题三解决过程:其实这个int型变量termType就是在程序中判断操作符和操作数的一个中间值,在PostfixEvaluator中也有体现.
代码调试过程中的问题和解决过程
-
问题一:对于AVL树的实现存在一些问题,原本以为书上所给的代码已经实现了AVL树,就好像那个
addElement(T element)一样。 -
问题一解决过程:询问了结对伙伴,发现好像不是这样的,
addElement(T element)这个方法只能一直添加元素,但不能使得元素成为平衡树,就好像如果一直利用这个方法添加递减的元素会导致蜕化树的出现 -
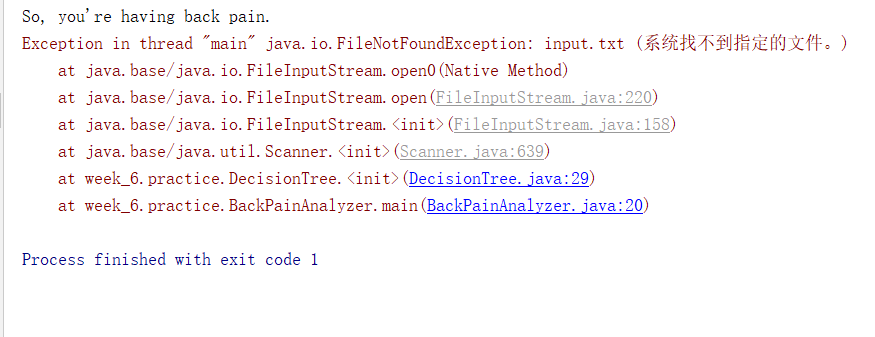
问题二:在运行代码时出现如图所示错误
![]()
-
问题二解决过程:在自己几次修改代码无果后求助同学,最后在其中加上路径解决问题
代码托管

上周考试课题总结
- 错题一:Which of the following is not a valid postfix expression?
A .5 4 +
B .6 5 4 + -
C .4 + 5
D .8 2 + 2 /
E .all of the above are valid postfix expressions
答案:C
解析:选项c是中缀符号,而不是后缀。 - 错题二:In an ideal implementations of a stack and a queue, all operations are ______________________ .
A .O(1)
B .O(n)
C .O(n log n)
D .O(n2)
E .it depends on the operation
答案:A
解析:
在堆栈和队列的良好实现中,所有操作都需要固定的时间。 - 错题三:A postfix expression can be easily evaluated using a queue.
A .true
B .false
答案:B
解析:后缀表达式可以很容易地使用堆栈来表示。 - 错题四:It is possible to implement a stack and a queue in such a way that all operations take a constant amount of time.
A .true
B .false
答案:A
解析:堆栈和队列的理想实现要求所有操作都需要恒定的时间量。
结对及互评
- 基于评分标准,我给本博客打分:15分 得分情况如下:
1.正确使用Markdown语法(加1分)
2.模板中的要素齐全(加1分)
3.教材学习中的问题和解决过程(加2分)
4.代码调试中的问题和解决过程(加3分)
5.感想,体会不假大空(加1分)
6.排版精美(加1分)
7.进度条中记录学习时间与改进情况(加1分)
8.有动手写新代码(加1分)
9.错题学习深入(加1分)
10.点评认真,能指出博客和代码中的问题(加1分)
11.结对学习情况真实可信(加1分)
12.本周有效代码超过300分行(加2分)
点评过的同学博客和代码
- 本周结对学习情况
20182306
学习进度条
| 代码行数(新增/累积) | 博客量(新增/累积) | 学习时间(新增/累积) | 重要成长 | |
|---|---|---|---|---|
| 目标 | 10000行 | 30篇 | 400小时 | |
| 第一周 | 171/171 | 2/2 | 20/20 | |
| 第二三周 | 415/586 | 3/5 | 42/62 | |
| 第四周 | 587/1173 | 2/7 | 22/84 | |
| 第五周 | 1706/2879 | 2/9 | 19/103 | |
| 第六周 | 1706/2879 | 2/9 | 19/103 | |
| 第七周 | 3969/6848 | 2/11 | 21/124 | |
| 第八周 | 1217/8065 | 2/13 | 24/148 | |
| 第九周 | 2396/10461 | 2/15 | 22/170 |


 浙公网安备 33010602011771号
浙公网安备 33010602011771号