【wqy】组合，容斥

组合

概念 Za

排列数：\(n\)个元素中选出\(m\)个元素 按一定顺序 \(\begin{align*}A^m_n=\frac{A!}{(n-m)!}\end{align*}\) (从\(n\)个人中选\(m\)个人来排队

组合数：\(n\)个不同元素中选\(m\)个元素组成一个集合 \(\begin{align*}C^m_n=\binom nm=\frac{A^m_n}{m!}=\frac{n!}{m!(n-m)!}\end{align*}\)

二项式定理：\(\begin{align*}(x+y)^n=\sum_{0\le k\le n}\binom nkx^ky_{n-k}\end{align*}\)

相关性质：

\(\begin{align*}2^n&=\sum_{i=0}^n\binom ni\ \ \ \binom n0=\binom nm=1\\\binom nm&=\binom{n-1}m+\binom{n-1}{m-1}\end{align*}\)

一个由计数对象组成的集合\(S\)，要计算它的大小\(|S|\)，考虑如果我们找到一
个集合\(T\)，使得\(S\)的元素与\(T\)的元素一一对应，那么\(|S|=|T|\)

推广： 如果\(S\)的每个元素对应到\(a\)个\(T\)中的元素，\(T\)的每个元素对应到\(b\)个\(S\)中的元
素，那么有：\(a|S|=b|T|,|S|=|T|*\frac ba\)
例子：\(n\)个元素的圆排列不好计算，但是一个圆排列枚举端点后会对应\(s\)个全排列，所以\(n\)个元素的圆排列数量就是\((n-1)!\) (即\(n!/n\)

\(Twelve\ Fold\ Way\)

你需要解决\(12\)个组合计数问题。
\(n\)个有标号/无标号的球放到\(m\)个有标号/无标号的盒子
盒子有三种限制：
A、无限制 ；B、每个盒子至少有一个球 ；C、 每个盒子至多有一个球
共有12种问题

为了方便，设\(U\)代表无标号，\(L\)代表有标号，这样一个问题就可以用
三个字母表示，第一个字母表示球是否有标号，第二个字母表示盒子是
否有标号，第三个字母表示限制。

1. (LLA) \(n\)个有标号的求放入\(m\)个有标号的盒子里

无限制 为每一个球选一个盒子放入 一个球有\(m\)种情况 \(ans=m^n\)

2. (ULC) \(n\)个无标号球放入\(m\)个有标号盒子里 至多放一个球

   即选\(n\)个盒子放球 \(ans=\binom mn\)

3. (LLC) \(n\)个有标号球放入\(m\)个有标号盒子 至多放一个

即一个排列问题 \(ans=\binom mn*n!=A(m,n)\)

4. (LUC) \(n\)个有标号球放入\(m\)个无标号盒子里 至多放一个

怎么放都是一样的 \(ans=(n\le m)\)

5. (UUC) \(n\)个无标号的球放入\(m\)个无标号盒 至多放一个

怎么放都是一样的 \(ans=(n\le m)\)

6. (ULB) \(n\)个无标号的球放入\(m\)个有标号盒 不允许有空盒

插板法：

相当于有\(n-1\)个间隔 从中选择\(m-1\)个位置插板 \(ans=\binom {n-1}{m-1}\)

7. (ULA) \(n\)个无标号的球放入\(m\)个有标号盒子 允许有空盒

如果再用插板法，板的位置可以重叠，不能直接计算。

上一个问题相当于有\(m\)个变量\(x_1,x_2,..,x_m\)，每一个变量都\(\ge1\)，求它们的和是\(n\)的解的数量

这个问题和上一个问题唯一区别为 每一个变量都\(\ge0\)

令\(y_i=x_i+1\) 求它们的和为\(n+m\) 转化为上一个问题 \(ans=\binom {n+m-1}{m-1}\)

8. (LLB) \(n\)个有标号的球放入\(m\)个有标号盒子 不允许有空盒

   容斥 枚举有\(i\)个盒子为空 转为LLA

   \(ans=\sum^m_{i=0}(-1)^i\binom mn(m-i)^n\)

9. (LUB) \(n\)个有标号的球放入\(m\)个无标号盒子 不允许有空盒

   这个问题的一个方案标号后会对应上一个问题LLB的\(m!\)种方案

   \(ans=\frac1{m!}\sum^m_{i=0}\binom mi(m-i)^n\) 即为第二类斯特林数

第二类斯特林数：\(S(n,k)\)，也记作\(\begin {Bmatrix} n \\ m\end {Bmatrix}\) 即有\(n\)个有区别小球，要放进\(m\)个相同盒子里，且每个盒子非空的方案数

\(\begin{Bmatrix}n\\m\end{Bmatrix}=\frac1{m!}\sum^m_{i=0}(-1)^i\binom mi(m-i)^n\)

考虑递推：\(S(n,m)=S(n-1,m-1)+m*S(n-1,m)\) 即讨论第\(n\)个球是否单独在一个盒子里 若不独占一个盒子 那就将其任放一个盒子里

​ 容斥：\(S(n,m)=\frac1{m!}\sum^m_{i=0}(-1)^i\binom mi(m-i)^n\) 即枚举空盒的个数 剩下随意放置 由于盒子相同最后要除以\(m!\) （这个柿子是一个卷积 可在\(O(nlogn)\)内求出

\(\begin{Bmatrix}0\\0\end{Bmatrix}=1\)，\(\begin{Bmatrix}n\\0\end{Bmatrix}=\begin{Bmatrix}0\\n\end{Bmatrix}=0\)

10. (LUA) \(n\)个有标号的球放入\(m\)个无标号盒子

    无限制 枚举有多少个盒子放了球\(ans=\begin{Bmatrix}n\\1\end{Bmatrix}+\begin{Bmatrix}n\\2\end{Bmatrix}+...+\begin{Bmatrix}n\\m\end{Bmatrix}\)

11. (UUB) \(n\)个无标号的球放入\(m\)个无标号盒子 不允许有空盒

    DP

    设\(f_{i,j}\)表示将\(i\)个球放到\(j\)个盒子里面的方案数。注意因为盒子没有标号，所以需要
    强制球的数量单调

    新开一个盒子，放入一个球：\(f_{i,j}\to f_{i+1,j+1}\)

    将现存的每一个盒子里都放入一个球：\(f_{i,j}\to f_{i+j,j}\)

    每一个方案都可以通过这两种转移得到，同时每一种方案的操作顺序都唯一，所
    以这个DP求出的就是解

    这个数列也有名字，叫做划分数：\(p_{n,m}=p_{n-1,m-1}+p_{n-m,m}\)

12. (UUA) \(n\)个无标号的球放入\(m\)个无标号盒子

    法一：枚举有几个盒子放了球，\(ans=p_{n,1}+p_{n,2}+...+p_{n,m}\)

    法二：与插板法扩展到盒子为空的方法相同，每一个盒子都多放一个球进去，\(ans=p_{n+m,m}\)

总结

是否有标号	A	B	C
LL	\(m^n\)	\(S_{n,m}m!\)	\(\begin{align*}\binom mnn!\end{align*}\)
LU	\(\sum^m_{i=1}S_{n,i}\)	\(S_{n,m}\)	\([n\le m]\)
UL	\(\begin{align*}\binom {n+m-1}{m-1}\end{align*}\)	\(\begin{align*}\binom {n-1}{m-1}\end{align*}\)	\(\begin{align*}\binom mn\end{align*}\)
UU	\(p_{n+m,m}\)	\(p_{n,m}\)	\([n\le m]\)

\(\begin{align*} {n \choose m}&=\frac {n!}{(n-m)!m!}\\S_{n,m}&=\frac1{m!}\sum^m_{i=0}(-1)^i\binom mi(m-i)^n\\p_{n,m}&=p_{n-m,m}+p_{n-1,m-1}\end{align*}\)

卡特兰数

base ZA

\(C_0=1,C_{n+1}=\sum^n_{i=0}C_iC{n-i}\) 通项公式： \(C_n=\frac{1}{n+1}{2n\choose n}=\frac{(2n)!}{n!(n+1)!}={2n\choose n}-{2n\choose n-1}\)

\(C_n=\frac1{n+1}\binom {2n}n=\frac{(2n)!}{(n+1)!n!}=\Pi^n_{k=2}\frac{n+k}k\) 递推公式：\(C_n=C_{n-1}\frac{4n-2}{n+1}\)

\(1,1,2,5,14,42,132,429,1430,...\)

理解(？)：luoguP1004栈

\(n\)个数一次进栈 可随机出栈 球有多少种可能

设\(f[i]\)表示\(i\)个数有几种可能 \(f[0]=f[1]=1\)

设\(x\)为最后一个出栈的 则\(x\)有\(n\)种取值

\(x\)为最后一个出栈的 则可以将已经出栈的数分为两个部分：比\(x\)小的；比\(x\)大的

比\(x\)小的有\(x-1\)个 这些数全部出栈可能为\(f[x-1]\)；比\(x\)大的同理 可能为\(f[n-x]\)

所以 \(ans=f[0]*f[n-1]+f[1]*f[n-2]+...+f[n-1]*f[0]\)

int main(){
	rd(n);
	c[0]=c[1]=1;
	for(int i=2;i<=n;++i) c[i]=c[i-1]*((ll)(i<<2)-2)/((ll)i+1);
	printf("%lld",c[n]);
    return 0; 
}

应用

​ 长度为\(2n\)的合法的括号序列数量 有𝑛个非叶子节点的满二叉树的个数

​ 不越过对角线的路径条数 对角线不相交的情况下，将一个凸多边形分成三角形的方法数

​ 出栈方案数

​ \(n\)个\(+1\)和n个\(-1\)构成\(2n\)项，其部分和满足\(\begin{align*}\sum^{k\le 2n}_{i=1}a_i\ge0\end{align*}\)

不超过对角线的路径条数

​ 考虑容斥，总方案-超过对角线的路径条数。
​ 注意到，每一个超过对角线的路径都会碰到\(y=x+1\)这条直线

​ 把所有不合法的路径沿着这条直线翻过去：这样一条不合法的路径就对应了一条从\((-1,1)\)走到\((n,m)\)的路径，两者是等价的
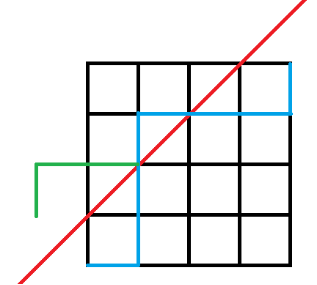\(\begin{align*}ans={2n\choose n}-{2n\choose n+1}=\frac{(2n)!}{n!(n-1)!}(\frac1n-\frac1{n+1})=\frac1{n+1}{2n\choose n}\end{align*}\)

容斥

base

容斥 \(\Big|\bigcup\limits_{i=1}^nS_i\Big|=\sum\limits_{m=1}^n(-1)^{m-1}\ \sum\limits_{a_i<a_{i+1}}\Big|\bigcap\limits_{i=1}^mS_{a_i}\Big|\)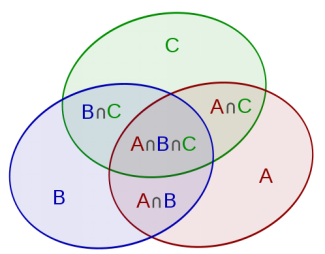

\(\begin{align*}|\bigcup_{i=1}^nA_i|=\sum^n_{i=1}|A_i|-\sum_{1\le i<j\le n}|A_i\cap A_j|+\end{align*}\)

\(\begin{align*}...+\sum_{1\le i<j<k\le n}|A_i\cap A_j\cap A_k|-...+(-1)^{n-1}|A_1\cap...\cap A_n|\end{align*}\)

else:(from gzy

对于全集 U 下的 集合的并 可以使用容斥原理计算，而集合的交则用全集减去 补集的并集

\(\begin{align*}\Big|\bigcap^n_{i=1}S_i\Big|=|U|-\Big|\bigcup^n_{i=1}\overline{S_i}\Big|\end{align*}\)

容斥原理一般有\(n\)个性质，满足第\(i\)个性质的元素集合为\(Ai\)，还有一个全集\(U\)

需要统计\(ans=|U \bigcap \overline A_1 \bigcap \overline A_2 \cdots \bigcap \overline A_n |\) \(ans=\sum_ {S \subseteq A}(-1)^{|S|}|U \bigcap S_ 1 \bigcap S_ 2 \cdots \bigcap S_ {|S|} |\)

用组合意义来说的话，\(x\in A_i\)是代表元素\(x\)具有性质\(i\)，我们要求的就是不具有所有性质的元素个数
用集合\(G_S\)来表示满足集合\(S\)中的所有性质，并且不满足集合\(\overline S\)中的所有性质的元素集合，即\(G _ S=\{ x|\forall A _ i\in S,x \in A _ i , \forall A _ i\in \overline S,x \notin A _ i \}\)
那么我们要求的就是\(G_{\varnothing}\)。
\(ans=\sum_ {S \subseteq A}(-1)^{|S|}|U \bigcap S_ 1 \bigcap S_ 2 \cdots \bigcap S_ {|S|} |\)
不难得知
\(\sum_{T \subseteq S,S \neq \varnothing} (-1)^{|S|} = \begin{cases} 1\quad (T = \varnothing)\\ 0\quad (otherwise) \end{cases}\)
证明：\(ans=\sum_ {S \subseteq A}(-1)^{|S|}|U \bigcap S_ 1 \bigcap S_ 2 \cdots \bigcap S_ {|S|} |\sum_{G_T} \sum_{T \subseteq S,S \neq \varnothing} (-1)^{|S|}=G_{\varnothing}\)

不定方程非负整数解计数

不定方程\(\sum^m_{i=1} x_i=n\)和\(m\)个限制条件\(l_i\le x_i\le r_i\)，求非负整数解的个数

没有限制时 不定方程\(\sum^m_{i=1}x_i=n\)非负整数解的个数为：\(C_{m+n-1}^{m-1}\) (证明：插板法

可以将\(n-\sum l_i\)，这样就变成了每一个元素都有一个上界的问题

设\(N=n-\sum l_i,\ b_i=r_i-l_i\)

枚举子集进行容斥。首先枚举一个集合里面不满足上界，这样我们就需要强制这个集合里面的数字不满足上界，也就是上界变成了下界。

\(\begin{align*}ans=\sum_s(-1)^{|S|}{N-\sum_{i\in S}b_i+m-1\choose m-1}\end{align*}\) \(O(m2^m)\)(==自行感悟 ) \(N\)比较小时可以DP

一个题：

[HAOI2008]硬币购物

即可转化为求方程\(\sum_{i-1}^4\ C_ix_i=S,x_i\le D_i\)的非负整数解的个数

最后求解\(\sum\limits_{i=1}^4C_ix_i=S-\sum\limits_{i=1}^kC_{a_i}(D_{a_i}+1)\)

 int main(){
	f[0]=1;
    for(int i=1;i<=4;++i){
        rd(a[i]);
        for(int v=a[i];v<M;++v) f[v]+=f[v-a[i]];
    }
    int T;rd(T);
    while(T--){
        rd(d[1]),rd(d[2]),rd(d[3]),rd(d[4]),rd(s);
        ans=0;
        for(int i=1,m,bit;i<(1<<4);++i){//二进制枚举集合 
        	m=s,bit=0;
            for(int j=1;j<=4;++j)
                if((i>>(j-1))&1) m-=(d[j]+1)*a[j],++bit;
            if(m>=0) ans+=(bit%2*2-1)*f[m];//奇加偶减 
    	}
        printf("%lld\n",f[s]-ans);
    }
}

wqy自创

有一个\(1\)到\(n\)的排列\(p\)。
定义一个区间是好的，当且仅当这个区间的值域也是这个区间。
定义一个排列是不可分割的，当且仅当这个排列不能分成两个或以上的区间，使得这几个区间都是好的区间。
求存在多少个长度为𝑛的不可分割的排列。

设\(f_i\)表示长度为\(i\)的不可分割的排列的数量。
考虑容斥。注意到任意一个不合法的排列都一定存在一个数\(x\)，使得\([1,x]\)这个区间是好的，并且对于任意的\(y<x\),\([1,y]\)都不是好的
所以枚举𝑥，可以得到容斥的公式：\(f_n=n!-\sum^{n-1}_{i=1}f_i(n-i)!\) \(O(n^2)\)
用多项式求逆可以做到\(O(n\ log\ n)\)

练习

一张\(n\times m\)的网格纸，求从左下走到右上的方案数，每次只能往右走或
者往上走。
答案就是\(\begin{align*}\binom {n+m}n\end{align*}\)，也就是说总共需要走\(n+m\)次，其中有\(n\)次是往上走的

ACG001E BBQ Hard

给定两个数组 求\(\begin{align*}\sum_{i=1}^n\sum_{j=i+1}^n\binom{a_i+b_i+a_j+b_j}{a_i+a_j} \end{align*}\)

由上面可以将\(\begin{align*}\binom{a_i+b_i+a_j+b_j}{a_i+a_j}\end{align*}\)转化为从点\((-b_i,-a_i)\)走到\((b_j,a_j)\)

\(f[i][j]\)即为各个起点走到它的方案数 递推可得

然后\(ans+=\sum_{i=1}^nf[a[i]][b[i]]\) 再减去自己走到自己的情况 最后除\(2\)

注意阶乘预处理要处理\(M<<2\)

==把组合变为走格子的形式很有用吖！

void Mod(ll &x){x=(x>=P)?x-P:x;}
ll C(int x,int y){return (fac[x]*ifac[y]%P)*ifac[x-y]%P;}
ll qpow(ll x,ll y){
	ll ret=1ll;
	while(y){
		if(y&1) ret=ret*x%P;
		x=x*x%P,y>>=1;
	}
	return ret;
}

int main(){
#ifndef ONLINE_JUDGE
    freopen("in.txt","r",stdin);
#endif
	rd(n);
	for(int i=1;i<=n;++i) rd(a[i]),rd(b[i]),++f[M-a[i]][M-b[i]];
	for(int i=1;i<=(M<<1);++i)
		for(int j=1;j<=(M<<1);++j)
			f[i][j]+=f[i-1][j],Mod(f[i][j]),f[i][j]+=f[i][j-1],Mod(f[i][j]);
	fac[0]=fac[1]=1ll;
	for(int i=2;i<=(M<<2);++i) fac[i]=fac[i-1]*(ll)i%P;
	ifac[M<<2]=qpow(fac[M<<2],P-2);
	for(int i=(M<<2);i;--i) ifac[i-1]=ifac[i]*i%P;
	for(int i=1;i<=n;++i) ans+=f[M+a[i]][M+b[i]],Mod(ans),ans+=(P-C(((a[i]+b[i])<<1),(a[i]<<1))),Mod(ans);
	printf("%lld",ans*inv2%P);
    return 0; 
}