【2003年集训队论文】王知昆《浅谈用极大化思想解决最大子矩形问题》
我把03年集训队王知昆的论文搬上来辽
王知昆《浅谈用极大化思想解决最大子矩形问题》
王知昆《浅谈用极大化思想解决最大子矩形问题》
【摘要】
本文针对一类近期经常出现的有关最大（或最优）子矩形及相关变形问题，介绍了极大化思想在这类问题中的应用。分析了两个具有一定通用性的算法。并通过一些例题讲述了这些算法选择和使用时的一些技巧。
【关键字】矩形，障碍点，极大子矩形
一、问题
最大子矩形问题：在一个给定的矩形网格中有一些障碍点，要找出网格内部不包含任何障碍点，且边界与坐标轴平行的最大子矩形。
二、定义和说明
首先明确一些概念。
1、定义有效子矩形为内部不包含任何障碍点且边界与坐标轴平行的子矩形。如图所示，第一个是有效子矩形（尽管边界上有障碍点），第二个不是有效子矩形（因为内部含有障碍点）。
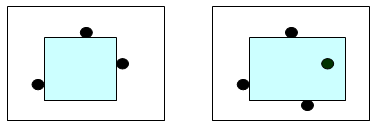
2、极大有效子矩形：一个有效子矩形，如果不存在包含它且比它大的有效子矩形，就称这个有效子矩形为极大有效子矩形。（为了叙述方便，以下称为极大子矩形）
3、定义最大有效子矩形为所有有效子矩形中最大的一个（或多个）。以下简称为最大子矩形。
三、 极大化思想
【定理1】在一个有障碍点的矩形中的最大子矩形一定是一个极大子矩形。
证明：如果最大子矩形A不是一个极大子矩形，那么根据极大子矩形的定义，存在一个包含A且比A更大的有效子矩形，这与“A是最大子矩形”矛盾，所以【定理1】成立。
四、从问题的特征入手，得到两种常用的算法
定理1虽然很显然，但却是很重要的。根据定理1，我们可以得到这样一个解题思路：通过枚举所有的极大子矩形，就可以找到最大子矩形。下面根据这个思路来设计算法。
约定：为了叙述方便，设整个矩形的大小为n×m，其中障碍点个数为s。
算法1
时间复杂度：O(S2)
空间复杂度：O(S)
算法的思路是通过枚举所有的极大子矩形找出最大子矩形。根据这个思路可以发现，如果算法中有一次枚举的子矩形不是有效子矩形、或者不是极大子矩形，那么可以肯定这个算法做了“无用功”，这也就是需要优化的地方。怎样保证每次枚举的都是极大子矩形呢，我们先从极大子矩形的特征入手。
【定理2】：一个极大子矩形的四条边一定都不能向外扩展。更进一步地说，一个有效子矩形是极大子矩形的充要条件是这个子矩形的每条边要么覆盖了一个障碍点，要么与整个矩形的边界重合。
定理2的正确性很显然，如果一个有效子矩形的某一条边既没有覆盖一个障碍点，又没有与整个矩形的边界重合，那么肯定存在一个包含它的有效子矩形。根据定理2，我们可以得到一个枚举极大子矩形的算法。为了处理方便，首先在障碍点的集合中加上整个矩形四角上的点。每次枚举子矩形的上下左右边界（枚举覆盖的障碍点），然后判断是否合法（内部是否有包含障碍点）。这样的算法时间复杂度为O(S5)，显然太高了。考虑到极大子矩形不能包含障碍点，因此这样枚举4个边界显然会产生大量的无效子矩形。
考虑只枚举左右边界的情况。对于已经确定的左右边界，可以将所有处在这个边界内的点按从上到下排序，如图1中所示，每一格就代表一个有效子矩形。这样做时间复杂度为O(S3)。由于确保每次得到的矩形都是合法的，所以枚举量比前一种算法小了很多。但需要注意的是，这样做枚举的子矩形虽然是合法的，然而不一定是极大的。所以这个算法还有优化的余地。通过对这个算法不足之处的优化，我们可以得到一个高效的算法。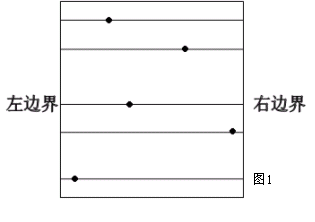
回顾上面的算法，我们不难发现，所枚举的矩形的上下边界都覆盖了障碍点或者与整个矩形的边界重合，问题就在于左右边界上。只有那些左右边界也覆盖了障碍点或者与整个矩形的边界重合的有效子矩形才是我们需要考察的极大子矩形，所以前面的算法做了不少“无用功”。怎么减少“无用功”呢，这里介绍一种算法（算法1），它可以用在不少此类题目上。
算法的思路是这样的，先枚举极大子矩形的左边界，然后从左到右依次扫描每一个障碍点，并不断修改可行的上下边界，从而枚举出所有以这个定点为左边界的极大子矩形。考虑如图2中的三个点，现在我们要确定所有以1号点为左边界的极大矩形。先将1号点右边的点按横坐标排序。然后按从左到右的顺序依次扫描1号点右边的点，同时记录下当前的可行的上下边界。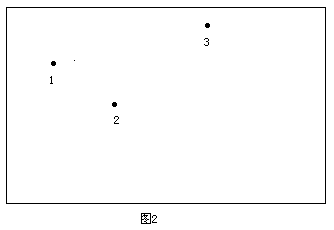
开始时令当前的上下边界分别为整个矩形的上下边界。然后开始扫描。第一次遇到2号点，以2号点作为右边界，结合当前的上下边界，就得到一个极大子矩形（如图3）。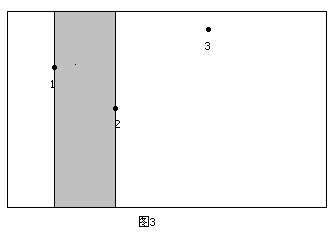
同时，由于所求矩形不能包含2号点，且2号点在1号点的下方，所以需要修改当前的下边界，即以2号点的纵坐标作为新的下边界。第二次遇到3号点，这时以3号点的横坐标作为右边界又可以得到一个满足性质1的矩形（如图4）。
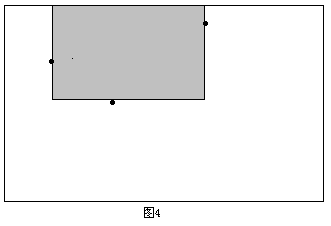类似的，需要相应地修改上边界。以此类推，如果这个点是在当前点（确定左边界的点）上方，则修改上边界；如果在下方，则修改下边界；如果处在同一行，则可中止搜索（因为后面的矩形面积都是0了）。由于已经在障碍点集合中增加了整个矩形右上角和右下角的两个点，所以不会遗漏右边界与整个矩形的右边重合的极大子矩形（如图5）。
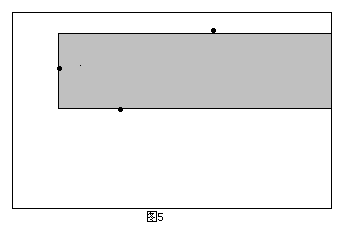需要注意的是，如果扫描到的点不在当前的上下边界内，那么就不需要对这个点进行处理。
这样做是否将所有的极大子矩形都枚举过了呢？可以发现，这样做只考虑到了左边界覆盖一个点的矩形，因此我们还需要枚举左边界与整个矩形的左边界重合的情况。这还可以分为两类情况。一种是左边界与整个举行的左边界重合，而右边界覆盖了一个障碍点的情况，对于这种情况，可以用类似的方法从右到左扫描每一个点作为右边界的情况。另一种是左右边界均与整个矩形的左右边界重合的情况，对于这类情况我们可以在预处理中完成：先将所有点按纵坐标排序，然后可以得到以相邻两个点的纵坐标为上下边界，左右边界与整个矩形的左右边界重合的矩形，显然这样的矩形也是极大子矩形，因此也需要被枚举到。
通过前面两步，可以枚举出所有的极大子矩形。算法1的时间复杂度是O(S2)。这样，可以解决大多数最大子矩形和相关问题了。
虽然以上的算法（算法1）看起来是比较高效的，但也有使用的局限性。可以发现，这个算法的复杂度只与障碍点的个数s有关。但对于某些问题，s最大有可能达到n×m，当s较大时，这个算法就未必能满足时间上的要求了。能否设计出一种依赖于n和m的算法呢？这样在算法1不能奏效的时候我们还有别的选择。我们再重新从最基本的问题开始研究。
算法2
时间复杂度：O(NM)
空间复杂度：O(S)
首先，根据定理1：最大有效子矩形一定是一个极大子矩形。不过与前一种算法不同的是，我们不再要求每一次枚举的一定是极大子矩形而只要求所有的极大子矩形都被枚举到。看起来这种算法可能比前一种差，其实不然，因为前一种算法并不是完美的：虽然每次考察的都是极大子矩形，但它还是做了一定量的“无用功”。可以发现，当障碍点很密集的时候，前一种算法会做大量没用的比较工作。要解决这个问题，我们必须跳出前面的思路，重新考虑一个新的算法。注意到极大子矩形的个数不会超过矩形内单位方格的个数，因此我们有可能找出一种时间复杂度是O(N×M)的算法。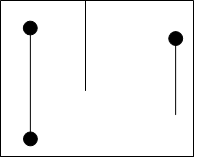
定义：
有效竖线：除了两个端点外，不覆盖任何障碍点的竖直线段。
悬线：上端点覆盖了一个障碍点或达到整个矩形上端的有效竖线。如图所示的三个有效竖线都是悬线。
对于任何一个极大子矩形，它的上边界上要么有一个障碍点，要么和整个矩形的上边界重合。那么如果把一个极大子矩形按x坐标不同切割成多个（实际上是无数个）与y轴垂直的线段，则其中一定存在一条悬线。而且一条悬线通过尽可能地向左右移动恰好能得到一个子矩形（未必是极大子矩形，但只可能向下扩展）。通过以上的分析，我们可以得到一个重要的定理。
【定理3】：如果将一个悬线向左右两个方向尽可能移动所得到的有效子矩形称为这个悬线所对应的子矩形，那么所有悬线所对应的有效子矩形的集合一定包含了所有极大子矩形的集合。
定理3中的“尽可能”移动指的是移动到一个障碍点或者矩形边界的位置。
根据【定理3】可以发现，通过枚举所有的悬线，就可以枚举出所有的极大子矩形。由于每个悬线都与它底部的那个点一一对应，所以悬线的个数＝(n-1)×m（以矩形中除了顶部的点以外的每个点为底部，都可以得到一个悬线，且没有遗漏）。如果能做到对每个悬线的操作时间都为O(1)，那么整个算法的复杂度就是O(NM)。这样，我们看到了解决问题的希望。
现在的问题是，怎样在O(1)的时间内完成对每个悬线的操作。我们知道，每个极大子矩形都可以通过一个悬线左右平移得到。所以，对于每个确定了底部的悬线，我们需要知道有关于它的三个量：顶部、左右最多能移动到的位置。对于底部为(i,j)的悬线，设它的高为hight[i,j],左右最多能移动到的位置为left[i,j],right[i,j]。为了充分利用以前得到的信息，我们将这三个函数用递推的形式给出。
对于以点(i,j)为底部的悬线：
如果点(i－1,j)为障碍点，那么，显然以(i,j)为底的悬线高度为1，而且左右均可以移动到整个矩形的左右边界，即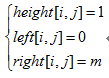
如果点(i－1,j)不是障碍点，那么，以(i,j)为底的悬线就等于以(i-1,j)为底的悬线＋点(i,j)到点(i-1,j)的线段。因此，height[i,j]=height[i-1,j]+1。比较麻烦的是左右边界，先考虑left[i,j]。如下图所示，(i,j)对应的悬线左右能移动的位置要在(i-1,j)的基础上变化。
即left[i,j]=max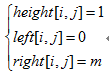
right[i,j]的求法类似。综合起来，可以得到这三个参数的递推式：
这样做充分利用了以前得到的信息，使每个悬线的处理时间复杂度为O(1)。对于以点(i,j)为底的悬线对应的子矩形，它的面积为(right[i,j]-left[i,j])*height[i,j]。
这样最后问题的解就是：
Result＝max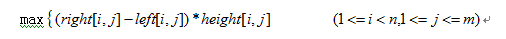
整个算法的时间复杂度为O(NM)，空间复杂度是O(NM)。
两个算法的对比：
以上说了两种具有一定通用性的处理算法，时间复杂度分别为O(S2)和O(NM)。两种算法分别适用于不同的情况。从时间复杂度上来看，第一种算法对于障碍点稀疏的情况比较有效，第二种算法则与障碍点个数的多少没有直接的关系（当然，障碍点较少时可以通过对障碍点坐标的离散化来减小处理矩形的面积，不过这样比较麻烦，不如第一种算法好），适用于障碍点密集的情况。
五、例题
1、Winter Camp2002,奶牛浴场
分析：
题目的数学模型就是给出一个矩形和矩形中的一些障碍点，要求出矩形内的最大有效子矩形。这正是我们前面所讨论的最大子矩形问题，因此前两种算法都适用于这个问题。
下面分析两种算法运用在本题上的优略：
对于第一种算法，不用加任何的修改就可以直接应用在这道题上，时间复杂度为O(S2)，S为障碍点个数；空间复杂度为O(S)。
对于第二种算法，需要先做一定的预处理。由于第二种算法复杂度与牛场的面积有关，而题目中牛场的面积很大（30000×30000），因此需要对数据进行离散化处理。离散化后矩形的大小降为S×S，所以时间复杂度为O(S2)，空间复杂度为O(S)。说明：需要注意的是，为了保证算法能正确执行，在离散化的时候需要加上S个点，因此实际需要的时间和空间较大，而且编程较复杂。
从以上的分析来看，无论从时空效率还是编程复杂度的角度来看，这道题采用第一种算法都更优秀。
附件中的程序(Pascal)
program happy;
var
f:text;
x,y:array[1..5002] of longint;
maxl,n,best,a,b,c,w,l,i,j,high,low:longint;
procedure sort(l,r:longint);
var
i,j:longint;
begin
i:=l+random(r-l+1);
a:=x[i]; b:=y[i]; i:=l; j:=r;
repeat
while (x[i]a) or ((x[j]=a) and (y[j]>b)) do j:=j-1;
if i<=j then
begin
c:=x[i]; x[i]:=x[j]; x[j]:=c;
c:=y[i]; y[i]:=y[j]; y[j]:=c;
inc(i); dec(j);
end;
until i>j;
if j>l then sort(l,j);
if ia) do j:=j-1;
if i<=j then
begin
c:=y[i]; y[i]:=y[j]; y[j]:=c;
inc(i); dec(j);
end;
until i>j;
if j>l then sort_y(l,j);
if ibest then best:=a;
end;
begin
assign(f,'happy.in');
reset(f);
readln(f,l,w);
readln(f,n);
for i:=1 to n do
readln(f,x[i],y[i]);
close(f);
inc(n); x[n]:=l; y[n]:=0;
inc(n); x[n]:=0; y[n]:=w;
sort(1,n);
best:=0;
for i:=1 to n do
begin
high:=w; low:=0; maxl:=l-x[i];
for j:=i+1 to n do
if (y[j]<=high) and (y[j]>=low) then
begin
if maxl*(high-low)<=best then break;
max((x[j]-x[i])*(high-low));
if y[j]=y[i] then break
else if y[j]>y[i] then
if y[j]low then low:=y[j];
end;
high:=w; low:=0; maxl:=l-x[i];
for j:=i-1 downto 1 do
if (y[j]<=high) and (y[j]>=low) then
begin
if maxl*(high-low)<=best then break;
max((x[i]-x[j])*(high-low));
if y[j]=y[i] then break
else if y[j]>y[i] then
if y[j]low then low:=y[j];
end;
end;
sort_y(1,n);
for i:=1 to n-1 do
max((y[i+1]-y[i])*l);
writeln(best);
end. 2、OIBH模拟赛1,提高组，Candy
题意简述：（原题见论文附件）
一个被分为 n*m 个格子的糖果盒，第 i 行第 j 列位置的格子里面有 a [i,j] 颗糖。但糖果盒的一些格子被老鼠洗劫。现在需要尽快从这个糖果盒里面切割出一个矩形糖果盒，新的糖果盒不能有洞，并且希望保留在新糖果盒内的糖的总数尽量多。
参数约定：1 ≤ n，m ≤ 1000
分析
首先需要注意的是：本题的模型是一个矩阵，而不是矩形。在矩阵的情况下，由于点的个数是有限的，所以又产生了一个新的问题：最大权值子矩阵。
定义：
有效子矩阵为内部不包含任何障碍点的子矩形。与有效子矩形不同，有效子矩阵地边界上也不能包含障碍点。
有效子矩阵的权值（只有有效子矩形才有权值）为这个子矩阵包含的所有点的权值和。
最大权值有效子矩阵为所有有效子矩阵中权值最大的一个。以下简称为最大权值子矩阵。
本题的数学模型就是正权值条件下的最大权值子矩阵问题。再一次利用极大化思想，因为矩阵中的权值都是正的，所以最大权值子矩阵一定是一个极大子矩阵。所以我们只需要枚举所有的极大子矩阵，就能从中找到最大权值子矩阵。同样，两种算法只需稍加修改就可以解决本题。下面分析两种算法应用在本题上的优略：
对于第一种算法，由于矩形中障碍点的个数是不确定的，而且最大有可能达到N×M,这样时间复杂度有可能达到O(N2M2)，空间复杂度为O(NM)。此外，由于矩形与矩阵的不同，所以在处理上会有一些小麻烦。
对于第二种算法，稍加变换就可以直接使用，时间复杂度为O(NM),空间复杂度为O（NM）。
可以看出，第一种算法并不适合这道题，因此最好还是采用第二种算法。
code
program candy;
const
maxn=1000;
var
left,right,high:array[1..maxn] of longint;
s:array[0..maxn,0..maxn] of longint;
now,res,leftmost,rightmost,i,j,k,n,m:longint;
f:text;
begin
assign(f,'candy.in');
reset(f);
readln(f,n,m);
fillchar(s,sizeof(s),0);
for i:=1 to m do
begin
left[i]:=1; right[i]:=m; high[i]:=0;
end;
res:=0;
for i:=1 to n do
begin
k:=0; leftmost:=1;
for j:=1 to m do
begin
read(f,now); k:=k+now;
s[i,j]:=s[i-1,j]+k;
if now=0 then
begin
high[j]:=0; left[j]:=1; right[j]:=m;
leftmost:=j+1;
end
else
begin
high[j]:=high[j]+1;
if leftmost>left[j] then left[j]:=leftmost;
end;
end;
rightmost:=m;
for j:=m downto 1 do
begin
if high[j]=0 then
begin
rightmost:=j-1;
end
else
begin
if right[j]>rightmost then right[j]:=rightmost;
now:=s[i,right[j]]+s[i-high[j],left[j]-1]-s[i-high[j],right[j]]-s[i,left[j]-1];
if now>res then res:=now;
end;
end;
end;
writeln(res);
end.3、Usaco Training, Section 1.5.4, Big Barn
题意简述（原题见论文附件）
Farmer John想在他的正方形农场上建一个正方形谷仓。由于农场上有一些树，而且Farmer John又不想砍这些树，因此要找出最大的一个不包含任何树的一块正方形场地。每棵树都可以看成一个点。
参数约定：牛场为N×N的，树的棵数为T。N≤1000,T≤10000。
code
program BigBarn;
var
d:array[1..1000,1..1000] of longint;
height,left,right:array[1..1000] of longint;
leftmost,rightmost,res,i,j,k,t,n:longint;
f:text;
begin
assign(f,'bigbrn.in');
reset(f);
readln(f,n,t);
fillchar(d,sizeof(d),0);
for i:=1 to t do
begin
readln(f,j,k);
d[j,k]:=1;
end;
close(f);
for i:=1 to n do
begin
height[i]:=0; left[i]:=1; right[i]:=n;
end;
res:=0;
for i:=1 to n do
begin
leftmost:=1;
for j:=1 to n do
if d[i,j]=1 then
begin
height[j]:=0; left[j]:=1; right[j]:=n;
leftmost:=j+1;
end
else
begin
height[j]:=height[j]+1;
if leftmost>left[j] then left[j]:=leftmost;
end;
rightmost:=n;
for j:=n downto 1 do
if d[i,j]=1 then rightmost:=j-1
else
begin
if rightmostres then res:=k;
end;
end;
assign(f,'bigbrn.out');
rewrite(f);
writeln(f,res);
close(f);
end. 分析：
这题是矩形上的问题，但要求的是最大子正方形。首先，明确一些概念。
1、定义有效子正方形为内部不包含任何障碍点的子正方形
2、定义极大有效子正方形为不能再向外扩展的有效子正方形，一下简称极大子正方形
3、定义最大有效子正方形为所有有效子正方形中最大的一个（或多个），以下简称最大子正方形。
本题的模型有一些特殊，要在一个含有一些障碍点的矩形中求最大子正方形。这与前两题的模型是否有相似之处呢？还是从最大子正方形的本质开始分析。
与前面的情况类似，利用极大化思想，我们可以得到一个定理：
【定理4】：在一个有障碍点的矩形中的最大有效子正方形一定是一个极大有效子正方形。
根据【定理4】,我们只需要枚举出所有的极大子正方形，就可以从中找出最大子正方形。极大子正方形有什么特征呢？所谓极大，就是不能再向外扩展。如果是极大子矩形，那么不能再向外扩展的充要条件是四条边上都覆盖了障碍点（【定理2】）。类似的，我们可以知道，一个有效子正方形是极大子正方形的充要条件是它任何两条相邻的边上都覆盖了至少一个障碍点。根据这一点，可以得到一个重要的定理。
【定理5】：每一个极大子正方形都至少被一个极大子矩形包含。且这个极大子正方形一定有两条不相邻的边与这个包含它的极大子矩形的边重合。
根据【定理5】,我们只需要枚举所有的极大子矩形，并检查它所包含的极大子正方形（一个极大子矩形包含的极大子正方形都是一样大的）是否是最大的就可以了。这样，问题的实质和前面所说的最大子矩形问题是一样的，同样的，所采用的算法也是一样的。
因为算法1和算法2都枚举出了所有的极大子矩形，因此，算法1和算法2都可以用在本题上。具体的处理方法如下：对于每一个枚举出的极大子矩形，如图所示，如果它的边长为a、b，那么它包含的极大子正方形的边长即为min(a,b)。
考虑到N和T的大小不同，所以不同的算法会有不同的效果。下面分析两种算法应用在本题上的优略。
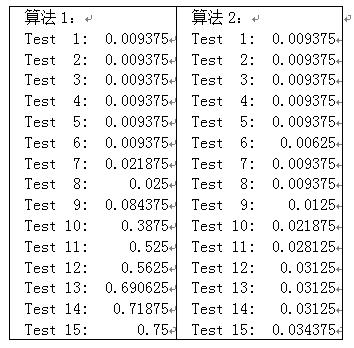
对于第一种算法，时间复杂度为O(T2)，对于第二种算法，时间复杂度为O(N2)。因为N<T，所以从时间复杂度的角度看，第二种算法要比第一种算法好。考虑到两个算法的空间复杂度都可以承受，所以选择第二种算法较好些。
以下是第一种和第二种算法编程实现后在USACO Training Program Gateway上的运行时间。可以看出，在数据较大时，算法2的效率比算法1高。
以上，利用极大化思想和前面设计的两个算法，通过转换模型，解决了三个具有一定代表性的例题。解题的关键就是如何利用极大化思想进行模型转换和如何选择算法。
六、小结
设计算法要从问题的基本特征入手，找出解题的突破口。本文介绍了两种适用于大部分最大子矩形问题及相关变型问题的算法，它们设计的突破口就是利用了极大化思想，找到了枚举极大子矩形这种方法。
在效率上，两种算法对于不同的情况各有千秋。一个是针对障碍点来设计的，因此复杂度与障碍点有关；另一个是针对整个矩形来设计的，因此复杂度与矩形的面积有关。虽然两个算法看起来有着巨大的差别，但他们的本质是相通的，都是利用极大化思想，从枚举所有的极大有效子矩形入手，找出解决问题的方法。
需要注意的是，在解决实际问题是仅靠套用一些现有算法是不够的，还需要对问题进行全面、透彻的分析,找出解题的突破口。
此外，如果采用极大化思想，前面提到的两种算法的复杂度已经不能再降低了，因为极大有效子矩形的个数就是O(NM)或O(S2)的。如果采用其他算法，理论上是有可能进一步提高算法效率，降低复杂度的。
