使用Python+TensorFlow2构建基于卷积神经网络（CNN）的ECG心电信号识别分类（三）

心电信号的噪声

EGG信号具有微弱、低幅值、低频、随杋性的特点，很容易被噪声干扰，而噪声可能来自生物体内，如呼吸、肌肉颤抖，也可能因为接触不良而引起体外干扰。是ECG信号主要的三种噪声为工频干扰、肌电干扰和基线漂移3，也是在滤波过程中急需被抑制去除的噪声干扰。

• 工频干扰：是由采集心电信号的设备周身的供电环境引起的电磁干扰，幅值低，噪声频率为50Hz左右，其波形很像一个正弦信号，该噪声常常会淹没有用的心电信号，也会影响P波和T波的检测。

• 肌电干扰：在心电图采集过程中，因为人体运动肌肉不自主颤抖造成，这种干扰无规律可言，波形形态会急速变化，频率很高，并且分布很广，范围在0-2000Hz内，能量集中在30-300Hz内，持续时间一般为50ms，肌电干扰与心电信号会重合在一起，这会导致有用的心电信号细微的变化很可能被忽视。

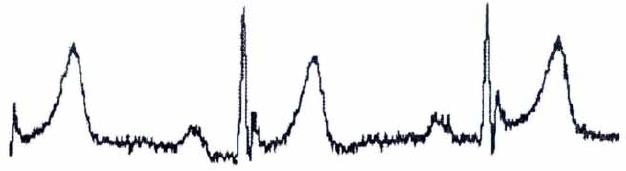
• 基线漂移：属于低频干扰，频率分布在0.15-0.3Hz内，由于电极位置的滑动变化或者人体的呼吸运动造成心电信号随时间缓慢变化而偏离正常基线位置产生基线漂移，幅度和频率都会时刻变化着。心电信号中的PR波段和ST波段非常容易受到影响产生失真。

心电信号的预处理

小波变换（Wavelet Transform, WT）可以进行时频变换，是对信号进行时域以及频域分析的最为理想工具。本文对含噪心电信号采用基于小波变换的去噪处理方法，分为以下3个步骤：

1. 由于噪声和信号混杂在一起，首先选择一个小波基函数，由于噪声和信号混杂在一起，所以要用小波变换对含噪心电信号进行某尺度分解得到各尺度上的小波系数。

2. 心电信号经过小波变换尺度分解后，幅值比较大的小波系数就是有用的信号，幅值比较小的小波系数就是噪声，根据心电信号和夹杂噪声的频率分布，对各尺度上的小波系数进行阈值处理，把小于阈值的小波系数置零或用阈值函数处理。

3. 分别处理完小波尺度分解后的低频系数和高频系数，再重构信号。

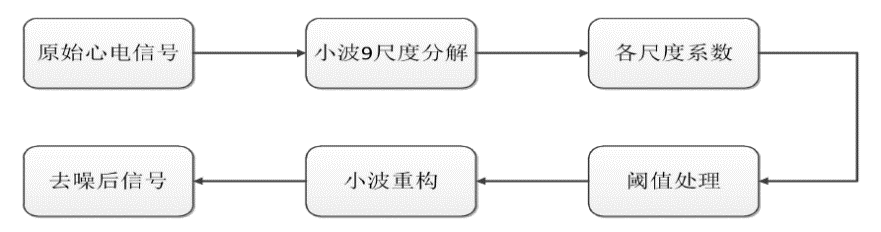
4尺度小波分解所得各尺度系数示意图如下，9尺度小波分解可以类比之：

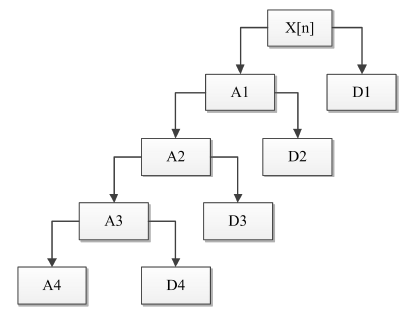
小波系数处理的阈值函数有硬阈值和软阈值之分。

1. 硬阈值函数：若分解后的系数绝对值大于阈值，保证其值不变；当其小于给定的阈值时，令其为零。

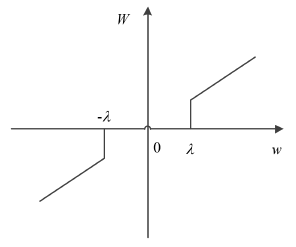
2. 软阈值函数：若分解后的系数绝对值大于阈值，令其值减去λ；当其小于给定的阈值时，令其为零。

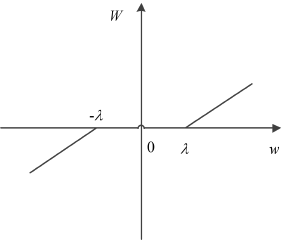
其中w为原始小波系数，W为处理后的小波系数，λ为给定的阈值，N为信号长度。λ的计算公式为
$$
\lambda=\frac{median|w|\sqrt{2lnN}}{0.6745}
$$

median为中位数

由上文分析可知，软阈值去噪法的小波系数在连续性上优于硬阈值法，故本文采取了软阈值法结合小波基对信号进行仿真实验。

关于小波变换的介绍可以参考这篇文章：https://blog.csdn.net/tbl1234567/article/details/52662985

代码实战

去噪理论大致如此，下面来实战编写代码。以编号为100的心电数据记录为例，上一篇文章已经通过wfdb将心电数据读取到了record变量中，record为一个大小为(65000,1)的numpy数组。要对其进行小波分解，首先要通过np.flatten()将其转换为shape=(65000,)的数组。

record = wfdb.rdrecord('ecg_data/' + 100, channel_names=['MLII'])
data = record.p_signal.flatten()

Python中使用pywt包进行信号的时频分析，其中包括傅里叶变换、小波变换等工具。使用pywt.wavedec()将时域信号进行9尺度变换到频域，小波基选用db5，返回值即为各尺度系数。

# 用db5作为小波基，对心电数据进行9尺度小波变换
coeffs = pywt.wavedec(data=data, wavelet='db5', level=9)
cA9, cD9, cD8, cD7, cD6, cD5, cD4, cD3, cD2, cD1 = coeffs

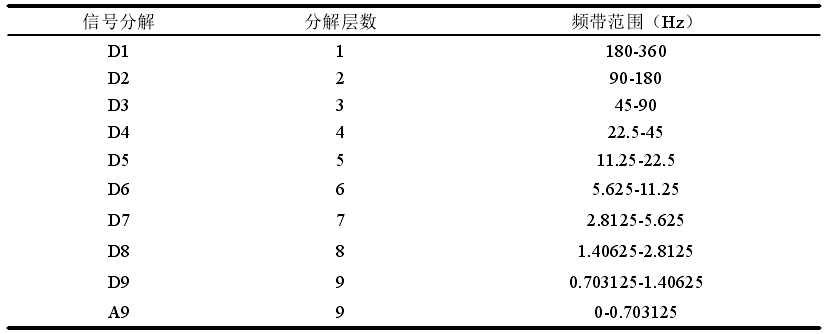
在对原始信号进行分解之后，我们可以知道，1-2层的细节分量的能量与原始信号的高频干扰保持一致。表明1-2层是高频噪声（工频干扰以及肌电噪声）集中的主要地方。因此我们需要滤除D1层和D2层的细节分量，通过将其置0来达到去除的目的。然后将信号分解得到的3~9层小波系数通过软阈值公式对信号的阈值进行处理。pywt.threshold()函数提供了阈值滤波功能，并且默认是mode='soft'的软阈值滤波。

threshold = (np.median(np.abs(cD1)) / 0.6745) * (np.sqrt(2 * np.log(len(cD1))))
# 将高频信号cD1、cD2置零
cD1.fill(0)
cD2.fill(0)
# 将其他中低频信号按软阈值公式滤波
for i in range(1, len(coeffs) - 2):
	coeffs[i] = pywt.threshold(coeffs[i], threshold)

最后对小波系数进行反变换，获得去噪后的信号。

rdata = pywt.waverec(coeffs=coeffs, wavelet='db5')

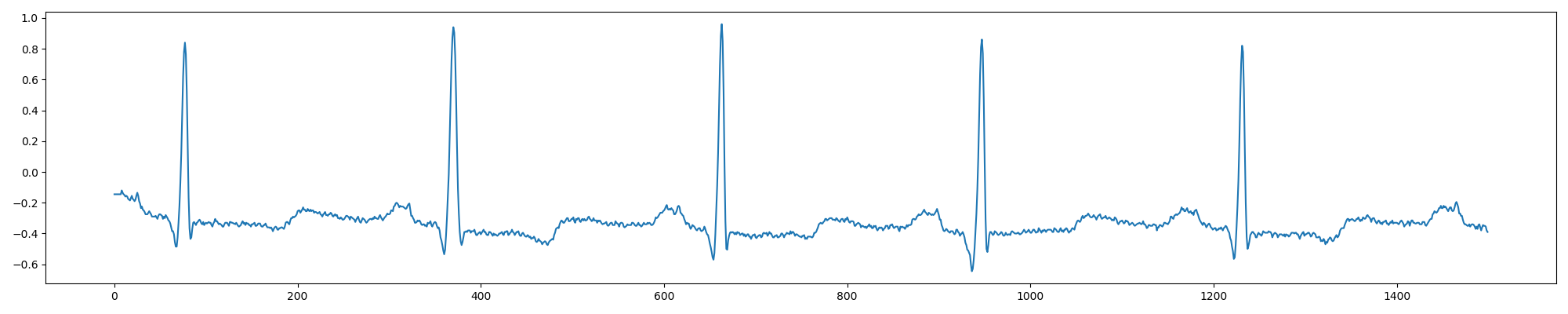
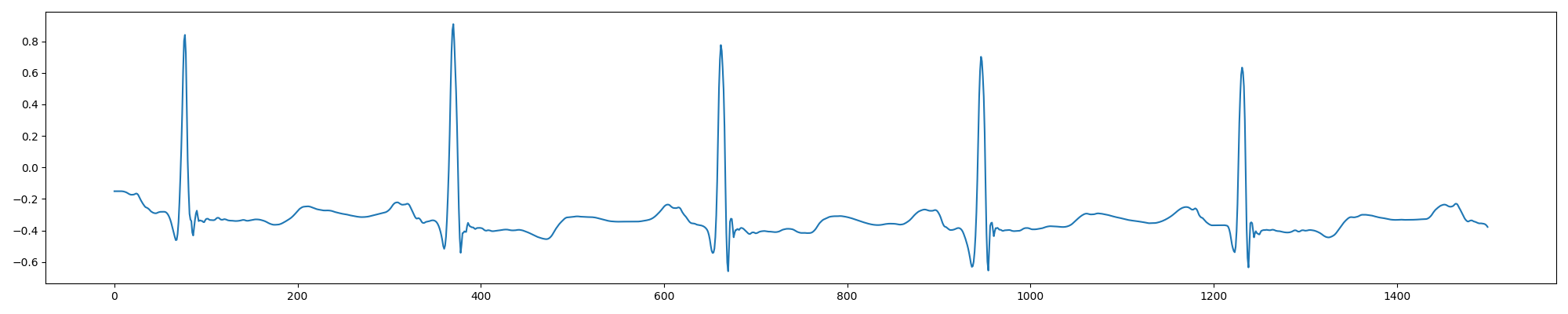
对预处理前后的100号信号截取前1500个信号点进行对比如下，可以看出降噪效果还是不错的：

plt.figure(figsize=(20, 4))
plt.plot(data)
plt.show()
plt.plot(rdata)
plt.show()