算法

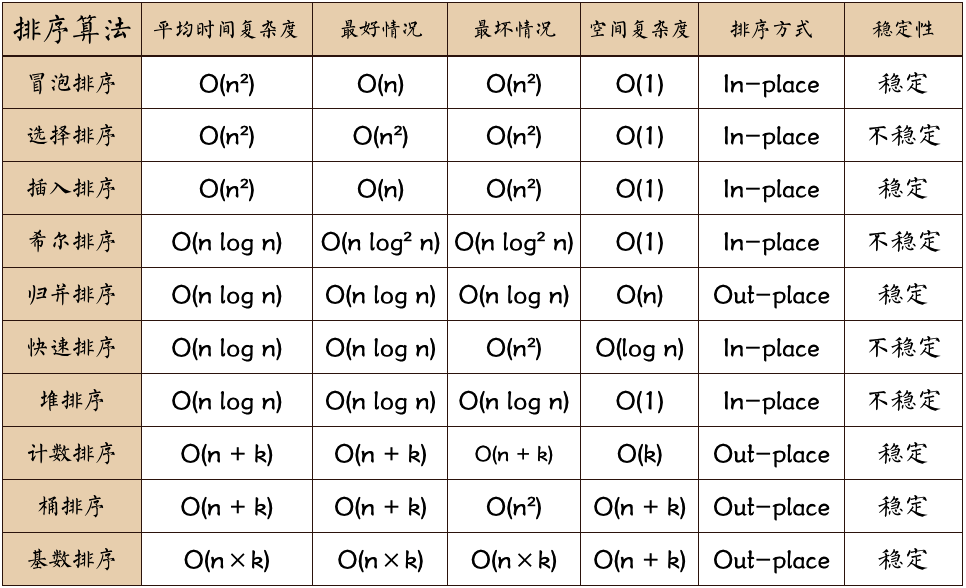
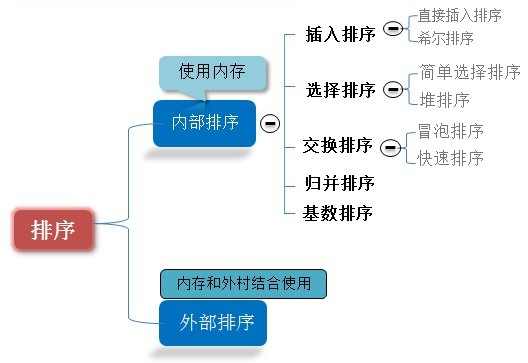
一、排序算法

1. 简单选择排序

表现最稳定的排序算法之一，因为无论什么数据进去都是O(n2)的时间复杂度，所以用到它的时候，数据规模越小越好。唯一的好处可能就是不占用额外的内存空间了吧。理论上讲，选择排序可能也是平时排序一般人想到的最多的排序方法了吧。

选择排序(Selection-sort)是一种简单直观的排序算法。它的工作原理：首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置，然后，再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。以此类推，直到所有元素均排序完毕。

n个记录的直接选择排序可经过n-1趟直接选择排序得到有序结果。具体算法描述如下：

• 初始状态：无序区为R[1..n]，有序区为空；
• 第i趟排序(i=1,2,3...n-1)开始时，当前有序区和无序区分别为R[1..i-1]和R(i..n）。该趟排序从当前无序区中-选出关键字最小的记录 R[k]，将它与无序区的第1个记录R交换，使R[1..i]和R[i+1..n)分别变为记录个数增加1个的新有序区和记录个数减少1个的新无序区；
• n-1趟结束，数组有序化了。

function selectionSort(arr) {
    var len = arr.length;
    var minIndex, temp;
    for (var i = 0; i < len - 1; i++) {
        minIndex = i;
        for (var j = i + 1; j < len; j++) {
            if (arr[j] < arr[minIndex]) {     //寻找最小的数
                minIndex = j;                 //将最小数的索引保存
            }
        }
        temp = arr[i];
        arr[i] = arr[minIndex];
        arr[minIndex] = temp;
    }
    console.timeEnd('选择排序耗时');
    return arr;
}
var arr=[3,44,38,5,47,15,36,26,27,2,46,4,19,50,48];
console.log(selectionSort(arr));//[2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]

2. 直接插入排序

插入排序（Insertion-Sort）的算法描述是一种简单直观的排序算法。它的工作原理是通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。插入排序在实现上，通常采用in-place排序（即只需用到O(1)的额外空间的排序），因而在从后向前扫描过程中，需要反复把已排序元素逐步向后挪位，为最新元素提供插入空间。

一般来说，插入排序都采用in-place在数组上实现。具体算法描述如下：

• 从第一个元素开始，该元素可以认为已经被排序；
• 取出下一个元素，在已经排序的元素序列中从后向前扫描；
• 如果该元素（已排序）大于新元素，将该元素移到下一位置；
• 重复步骤3，直到找到已排序的元素小于或者等于新元素的位置；
• 将新元素插入到该位置后；
• 重复步骤2~5。

function insertionSort(array) {
    if (Object.prototype.toString.call(array).slice(8, -1) === 'Array') {
        console.time('插入排序耗时：');
        for (var i = 1; i < array.length; i++) {
            var key = array[i];
            var j = i - 1;
            while (j >= 0 && array[j] > key) {
                array[j + 1] = array[j];
                j--;
            }
            array[j + 1] = key;
        }
        console.timeEnd('插入排序耗时：');
        return array;
    } else {
        return 'array is not an Array!';
    }
}

3. 冒泡排序

冒泡排序是一种简单的排序算法。它重复地走访过要排序的数列，一次比较两个元素，如果它们的顺序错误就把它们交换过来。走访数列的工作是重复地进行直到没有再需要交换，也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。

• 比较相邻的元素。如果第一个比第二个大，就交换它们两个；
• 对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对，这样在最后的元素应该会是最大的数；
• 针对所有的元素重复以上的步骤，除了最后一个；
• 重复步骤1~3，直到排序完成。

function bubbleSort3(arr3) {
    var low = 0;
    var high= arr.length-1; //设置变量的初始值
    var tmp,j;
    while (low < high) {
        for (j= low; j< high; ++j) //正向冒泡,找到最大者
            if (arr[j]> arr[j+1]) {
                tmp = arr[j]; 
                arr[j]=arr[j+1];
                arr[j+1]=tmp;
            }
        --high;                 //修改high值, 前移一位
        for (j=high; j>low; --j) //反向冒泡,找到最小者
            if (arr[j]

4.快速排序

快速排序的基本思想：通过一趟排序将待排记录分隔成独立的两部分，其中一部分记录的关键字均比另一部分的关键字小，则可分别对这两部分记录继续进行排序，以达到整个序列有序。

快速排序使用分治法来把一个串（list）分为两个子串（sub-lists）。具体算法描述如下：

• 从数列中挑出一个元素，称为 "基准"（pivot）；
• 重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区退出之后，该基准就处于数列的中间位置。这个称为分区（partition）操作；
• 递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序。

/*方法说明：快速排序
@param  array 待排序数组*/

var arr=[3,44,38,5,47,15,36,26,27,2,46,4,19,50,48];

var quickSort=function(arr){
    if(arr.length <= 1){
        return arr;
    }
    var keyIndex=Math.floor(arr.length / 2);
    var key=arr.splice(keyIndex,1)[0];
    var left=[];
    var right=[];
    for(var i=0;i<arr.length;i++){
        if(arr[i] < index){
            left.push(arr[i]);
        }else {
            right.push(arr[i]);
        }
    }
    
    return quickSort(left).concat([index],quickSort(right);
}

5. 希尔排序

希尔排序是希尔（Donald Shell）于1959年提出的一种排序算法。希尔排序也是一种插入排序，它是简单插入排序经过改进之后的一个更高效的版本，也称为缩小增量排序，同时该算法是冲破O(n2）的第一批算法之一。它与插入排序的不同之处在于，它会优先比较距离较远的元素。希尔排序又叫缩小增量排序。

希尔排序是把记录按下表的一定增量分组，对每组使用直接插入排序算法排序；随着增量逐渐减少，每组包含的关键词越来越多，当增量减至1时，整个文件恰被分成一组，算法便终止。

• 选择一个增量序列t1，t2，…，tk，其中ti>tj，tk=1；
• 按增量序列个数k，对序列进行k 趟排序；
• 每趟排序，根据对应的增量ti，将待排序列分割成若干长度为m的子序列，分别对各子表进行直接插入排序。仅增量因子为1 时，整个序列作为一个表来处理，表长度即为整个序列的长度。

function shellSort(arr) {
    var len = arr.length,
        temp,
        gap = 1;
    console.time('希尔排序耗时:');
    while(gap < len/5) {          //动态定义间隔序列
        gap =gap*5+1;
    }
    for (gap; gap > 0; gap = Math.floor(gap/5)) {
        for (var i = gap; i < len; i++) {
            temp = arr[i];
            for (var j = i-gap; j >= 0 && arr[j] > temp; j-=gap) {
                arr[j+gap] = arr[j];
            }
            arr[j+gap] = temp;
        }
    }
    console.timeEnd('希尔排序耗时:');
    return arr;
}
var arr=[3,44,38,5,47,15,36,26,27,2,46,4,19,50,48];
console.log(shellSort(arr));//[2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]

6. 堆排序

堆排序（Heapsort）是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构，并同时满足堆积的性质：即子结点的键值或索引总是小于（或者大于）它的父节点。

• 首先遍历数组，判断该节点的父节点是否比他小，如果小就交换位置并继续判断，直到他的父节点比他大 重新以上操作 1，直到数组首位是最大值
• 然后将首位和末尾交换位置并将数组长度减一，表示数组末尾已是最大值，不需要再比较大小
• 对比左右节点哪个大，然后记住大的节点的索引并且和父节点对比大小，如果子节点大就交换位置
• 重复以上操作 3 - 4 直到整个数组都是大根堆。

function heap(array) {
  checkArray(array);
  // 将最大值交换到首位
  for (let i = 0; i < array.length; i++) {
    heapInsert(array, i);
  }
  let size = array.length;
  // 交换首位和末尾
  swap(array, 0, --size);
  while (size > 0) {
    heapify(array, 0, size);
    swap(array, 0, --size);
  }
  return array;
}

function heapInsert(array, index) {
  // 如果当前节点比父节点大，就交换
  while (array[index] > array[parseInt((index - 1) / 2)]) {
    swap(array, index, parseInt((index - 1) / 2));
    // 将索引变成父节点
    index = parseInt((index - 1) / 2);
  }
}
function heapify(array, index, size) {
  let left = index * 2 + 1;
  while (left < size) {
    // 判断左右节点大小
    let largest =
      left + 1 < size && array[left] < array[left + 1] ? left + 1 : left;
    // 判断子节点和父节点大小
    largest = array[index] < array[largest] ? largest : index;
    if (largest === index) break;
    swap(array, index, largest);
    index = largest;
    left = index * 2 + 1;
  }
}

// 将 i 结点以下的堆整理为大顶堆，注意这一步实现的基础实际上是：
// 假设 结点 i 以下的子堆已经是一个大顶堆，heap_adjust函数实现的
// 功能是实际上是：找到 结点 i 在包括结点 i 的堆中的正确位置。后面将写一个 for 循环，从第一个非叶子结点开始，对每一个非叶子结点都执行 heap_adjust操作，所以就满足了结点 i 以下的子堆已经是一大顶堆
function heap_adjust(arr, start, end){
　　var temp = arr[start],
　　j = start*2;
      // j<end 的目的是对结点 i 以下的结点全部做顺序调整
　　for(;j < end; j *= 2){
　　　　if(arr[j] < arr[j+1]){
　　　　　　j++;// 找到两个孩子中较大的一个，再与父节点比较
　　　　}
　　　　if(temp > arr[j]){
　　　　　　break;
　　　　}
　　　　arr[start] = arr[j];
　　　　start = j;// 交换后，temp 的下标变为 j
　　}
　　arr[start] = temp;
}
function heap_sort(arr){
      // 初始化大顶堆，从第一个非叶子结点开始
　　var len = arr.length;
　　for(var i = len/2; i >= 0; i--){
　　　　heap_adjust(arr, i, len);
　　}
      // 排序，每一次for循环找出一个当前最大值，数组长度减一
　　for(var i = len; i > 0; i--){
　　　　swap(arr, 0, i -1);// 根节点与最后一个节点交换
           // 从根节点开始调整，并且最后一个结点已经为当前最大值，不需要再参与比较，所以第三个参数为 i，即比较到最后一个结点前一个即可 
　　　　heap_adjust(arr, 0, i);
　　}
}
function swap(arr, i, j){
　　var temp = arr[i];
　　arr[i] = arr[j];
　　arr[j] = temp;
}

7. 归并排序

和选择排序一样，归并排序的性能不受输入数据的影响，但表现比选择排序好的多，因为始终都是O(n log n）的时间复杂度。代价是需要额外的内存空间。

归并排序是建立在归并操作上的一种有效的排序算法。该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。归并排序是一种稳定的排序方法。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为2-路归并。

• 把长度为n的输入序列分成两个长度为n/2的子序列；
• 对这两个子序列分别采用归并排序；
• 将两个排序好的子序列合并成一个最终的排序序列。

function mergeSort(arr) {
    const length = arr.length;
    if (length === 1) { //递归算法的停止条件，即为判断数组长度是否为1
        return arr;
    }
    const mid = Math.floor(length / 2);
    const left = arr.slice(0,  mid);
    const right = arr.slice(mid, length);
    return merge(mergeSort(left), mergeSort(right)); //要将原始数组分割直至只有一个元素时，才开始归并
}
function merge(left, right) {
    const result = [];
    let il = 0;
    let ir = 0;
    //left, right本身肯定都是从小到大排好序的
    while( il < left.length && ir < right.length) {
        if (left[il] < right[ir]) {
            result.push(left[il]);
            il++;
        } else {
            result.push(right[ir]);
            ir++;
        }  
    }
    //不可能同时存在left和right都有剩余项的情况, 要么left要么right有剩余项, 把剩余项加进来即可
    while (il < left.length) { 
        result.push(left[il]);
        il++;
    }
    while(ir < right.length) {
        result.push(right[ir]);
        ir++;
    }
    return result;
}

本部分摘自：https://blog.csdn.net/hellozhxy/article/details/79911867

二、动态规划，参见背包问题

动态规划的原理
动态规划与分治法类似，都是把大问题拆分成小问题，通过寻找大问题与小问题的递推关系，解决一个个小问题，最终达到解决原问题的效果。但不同的是，分治法在子问题和子子问题等上被重复计算了很多次，而动态规划则具有记忆性，通过填写表把所有已经解决的子问题答案纪录下来，在新问题里需要用到的子问题可以直接提取，避免了重复计算，从而节约了时间，所以在问题满足最优性原理之后，用动态规划解决问题的核心就在于填表，表填写完毕，最优解也就找到。

最优性原理是动态规划的基础，最优性原理是指“多阶段决策过程的最优决策序列具有这样的性质：不论初始状态和初始决策如何，对于前面决策所造成的某一状态而言，其后各阶段的决策序列必须构成最优策略”。

背包问题

在解决问题之前，为描述方便，首先定义一些变量：Vi表示第 i 个物品的价值，Wi表示第 i 个物品的体积，定义V(i,j)：当前背包容量 j，前 i 个物品最佳组合对应的价值，同时背包问题抽象化（X1，X2，…，Xn，其中 Xi 取0或1，表示第 i 个物品选或不选）。

1、建立模型，即求max(V1X1+V2X2+…+VnXn)；

2、寻找约束条件，W1X1+W2X2+…+WnXn<capacity；

3、寻找递推关系式，面对当前商品有两种可能性：

包的容量比该商品体积小，装不下，此时的价值与前i-1个的价值是一样的，即V(i,j)=V(i-1,j)；
还有足够的容量可以装该商品，但装了也不一定达到当前最优价值，所以在装与不装之间选择最优的一个，即V(i,j)=max｛V(i-1,j)，V(i-1,j-w(i))+v(i)｝。
其中V(i-1,j)表示不装，V(i-1,j-w(i))+v(i) 表示装了第i个商品，背包容量减少w(i)，但价值增加了v(i)；

由此可以得出递推关系式：

• j<w(i)      V(i,j)=V(i-1,j)
• j>=w(i)     V(i,j)=max｛V(i-1,j)，V(i-1,j-w(i))+v(i)｝

/**
    * @param m : 表示背包的最大容量
    * @param n : 表示商品的个数
    * @param w : 表示商品重量数组
    * @param p : 表示商品价值数组
    * 
*/
public static int[][] DP_01bag(int m,int n,int w[],int p[]){
    //c[i][m] 表示前i件物品恰好放入重量为m的背包时的最大价值
    int c[][] = new int[n+1][m+1];
    for(int i=0;i<n+1;i++){
    c[i][0] = 0;
    }
    for(int j=0;j<m+1;j++){
    c[0][j] = 0;
    }
    for(int i=1;i<n+1;i++){
    　　for(int j=1;j<m+1;j++){
          //当物品为i件重量为j时，如果第i件的重量(w[i-1])小于重量j时，c[i][j]为下列两种情况之一：
         //(1)物品i不放入背包中，所以c[i][j]为c[i-1][j]的值
         //(2)物品i放入背包中，则背包剩余重量为j-w[i-1],所以c[i][j]为c[i-1][j-w[i-1]]的值加上当前物品i的价值    
        if(w[i-1] <= j){
            if(c[i-1][j] <c[i-1][j-w[i-1]]+p[i-1]){
            　　c[i][j] = c[i-1][j-w[i-1]]+p[i-1];
            　　}else{
                　　c[i][j] = c[i-1][j];
            　　}            
        　　 }
        }
    }
    return c;
}       

本部分参考：https://blog.csdn.net/qq_38410730/article/details/81667885         js版本实现

三、二叉树

 二叉树是n(n>=0)个结点的有限集合，该集合或者为空集（称为空二叉树），或者由一个根结点和两棵互不相交的、分别称为根结点的左子树和右子树组成。

由二叉树定义以及图示分析得出二叉树有以下特点：
1）每个结点最多有两颗子树，所以二叉树中不存在度大于2的结点。
2）左子树和右子树是有顺序的，次序不能任意颠倒。
3）即使树中某结点只有一棵子树，也要区分它是左子树还是右子树。

性质：

1）在二叉树的第i层上最多有2^i-1 个节点 。（i>=1）
2）二叉树中如果深度为k,那么最多有2^k-1个节点。(k>=1）
3）n₀=n₂+1 n₀表示度数为0的节点数，n₂表示度数为2的节点数。
4）在完全二叉树中，具有n个节点的完全二叉树的深度为[log₂n]+1，其中[log₂n]是向下取整。
5）若对含 n 个结点的完全二叉树从上到下且从左至右进行 1 至 n 的编号，则对完全二叉树中任意一个编号为 i 的结点有如下特性：

• 若 i=1，则该结点是二叉树的根，无双亲, 否则，编号为 [i/2] 的结点为其双亲结点;
• 若 2i>n，则该结点无左孩子， 否则，编号为 2i 的结点为其左孩子结点；
• 若 2i+1>n，则该结点无右孩子结点， 否则，编号为2i+1 的结点为其右孩子结点。

满二叉树：在一棵二叉树中。如果所有分支结点都存在左子树和右子树，并且所有叶子都在同一层上，这样的二叉树称为满二叉树。
满二叉树的特点有：
1）叶子只能出现在最下一层。出现在其它层就不可能达成平衡。
2）非叶子结点的度一定是2。
3）在同样深度的二叉树中，满二叉树的结点个数最多，叶子数最多。

完全二叉树：对一颗具有n个结点的二叉树按层编号，如果编号为i(1<=i<=n)的结点与同样深度的满二叉树中编号为i的结点在二叉树中位置完全相同，则这棵二叉树称为完全二叉树。

特点：
1）叶子结点只能出现在最下层和次下层。
2）最下层的叶子结点集中在树的左部。
3）倒数第二层若存在叶子结点，一定在右部连续位置。
4）如果结点度为1，则该结点只有左孩子，即没有右子树。
5）同样结点数目的二叉树，完全二叉树深度最小。
注：满二叉树一定是完全二叉树，但反过来不一定成立。

顺序存储：二叉树的顺序存储结构就是使用一维数组存储二叉树中的结点，并且结点的存储位置，就是数组的下标索引。

二叉排序树，又叫二叉查找树，它或者是一棵空树；或者是具有以下性质的二叉树：
1. 若它的左子树不空，则左子树上所有节点的值均小于它的根节点的值；
2. 若它的右子树不空，则右子树上所有节点的值均大于它的根节点的值；
3. 它的左右子树也分别为二叉排序树。

四、加油站问题(贪心算法)

贪心选择：在对问题求解时，总是做出在当前看来是最好的选择。也就是说，不从整体最优上加以考虑，他所做出的是在某种意义上的局部最优解。
最优子结构：当一个问题的最优解包含其子问题的最优解时，称此问题具有最优子结构性质。

问题：一辆汽车加满油后可行驶 n公里。旅途中有若干个加油站。设计一个有效算法，指出应 在哪些加油站停靠加油，使沿途加油次数最少。

输入：

第一行有 2 个正整数n和 k（k<=1000 )，表示汽车加满油后可行驶n公里，且旅途中有 k个加油站。 第二行有 k+1 个整数，表示第 k 个加油站与第k-1 个加油站之间的距离。 第 0 个加油站表示出发地，汽车已加满油。 第 k+1 个加油站表示目的地。

输出：

输出最少加油次数。如果无法到达目的地，则输出“No Solution!”。

输入样例：

7 7
1 2 3 4 5 1 6 6

输出样例：

4

分析：找到汽车满油量时可以行驶的最大路程范围内的最后一个加油站，加油后则继续用此方法前进。需要检查每一小段路程是否超过汽车满油量时的最大支撑路程。

function greedy(n,k) {
        var count=0;
        var arr =[];
        //随机分配arr的每个数，即第i和i-1个加油站之间的距离
        for (var i =0 ;i <=k;i++){
            arr[i] = parseInt(Math.random()*10+1);
        }
        console.log(arr);//5 8 6 1 9 10 8 4 3 6 9
        var  num=0;
        for(var j=0;j<=k;j++)
        {
            count+=arr[j];
            if(count>n)
            {
                num++;
                count=arr[j];
            }
        }
        console.log('汽车最少要需要加油的次数为：'+num);//8
        return ;
    }
    console.log(greedy(10,10));

本部分摘自：https://blog.csdn.net/m0_37686205/article/details/90115668

五、二分法

二分法查找，也称为折半法，是一种在有序数组中查找特定元素的搜索算法。

二分法查找的思路如下：

（1）首先，从数组的中间元素开始搜索，如果该元素正好是目标元素，则搜索过程结束，否则执行下一步。

（2）如果目标元素大于/小于中间元素，则在数组大于/小于中间元素的那一半区域查找，然后重复步骤（1）的操作。

（3）如果某一步数组为空，则表示找不到目标元素。

二分法查找的时间复杂度O(logn)。

//非递归
function binarySearch(arr,key){
    var low=0; //数组最小索引值
    var high=arr.length-1; //数组最大索引值
    while(low<=high){
        var mid=Math.floor((low+high)/2);
        if(key==arr[mid]){
            return mid;
        }else if(key>arr[mid]){
            low=mid+1;
        }else{
            high=mid-1;
        }
    }
    return -1; //low>high的情况，这种情况下key的值大于arr中最大的元素值或者key的值小于arr中最小的元素值
}
//递归
function binarySearch(arr,low,high,key){
    if(low>high){return -1;}
    var mid=Math.floor((low+high)/2);
    if(key==arr[mid]){
        return mid;
    }else if(key<arr[mid]){
        high=mid-1;
        return binarySearch(arr,low,high,key);
    }else{
        low=mid+1;
        return binarySearch(arr,low,high,key);
    }
}

六、二叉树遍历

1. 前序遍历

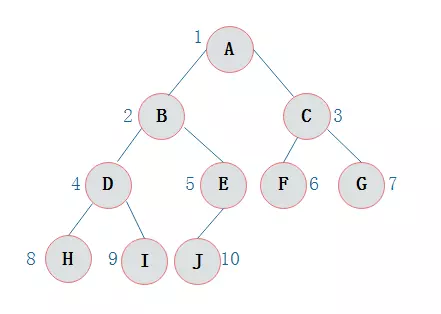
前序遍历通俗的说就是从二叉树的根结点出发，当第一次到达结点时就输出结点数据，按照先向左在向右的方向访问。

从根结点出发，则第一次到达结点A，故输出A;
继续向左访问，第一次访问结点B，故输出B；
按照同样规则，输出D，输出H；
当到达叶子结点H，返回到D，此时已经是第二次到达D，故不在输出D，进而向D右子树访问，D右子树不为空，则访问至I，第一次到达I，则输出I；
I为叶子结点，则返回到D，D左右子树已经访问完毕，则返回到B，进而到B右子树，第一次到达E，故输出E；
向E左子树，故输出J；
按照同样的访问规则，继续输出C、F、G；

二叉树的前序遍历输出为：
ABDHIEJCFG

先序递归遍历思路：先遍历根结点，将值存入数组，然后递归遍历：先左结点，将值存入数组，继续向下遍历；直到（二叉树为空）子树为空，则遍历结束；然后再回溯遍历右结点，将值存入数组，这样递归循环，直到（二叉树为空）子树为空，则遍历结束。

先序非递归遍历思路：

• 初始化一个栈，将根节点压入栈中；
• 当栈为非空时，循环执行步骤3到4，否则执行结束；
• 从队列取得一个结点（取的是栈中最后一个结点），将该值放入结果数组；
• 若该结点的右子树为非空，则将该结点的右子树入栈，若该结点的左子树为非空，则将该结点的左子树入栈；（注意：先将右结点压入栈中，后压入左结点，从栈中取得时候是取最后一个入栈的结点，而先序遍历要先遍历左子树，后遍历右子树）

//递归
let result = [];
let dfs = function (node) {
    if(node) {
        result.push(node.value);
        dfs(node.left);
        dfs(node.right);
    }
}
//非递归
let dfs = function (nodes) {
    let result = [];
    let stack = [];
    stack.push(nodes);
    while(stack.length) { // 等同于 while(stack.length !== 0) 直到栈中的数据为空
        let node = stack.pop(); // 取的是栈中最后一个j
        result.push(node.value);
        if(node.right) stack.push(node.right); // 先压入右子树
        if(node.left) stack.push(node.left); // 后压入左子树
    }
    return result;
}

/*
     * 1、有左儿子，入栈 
     * 2、无左儿子，自己出栈并看右儿子是否为空 
     * 3、右儿子为空，出栈 
     * 4、右儿子不为空，入栈 
     * 5、入栈时输出
     */
    public void preIterate(TreeNode<String> root) {
        Stack<TreeNode<String>> stack = new Stack<TreeNode<String>>();
        TreeNode<String> now = root;
        do {
            while (now != null) {
                System.out.print(now.getData() + " ");
                stack.push(now);
                now = now.getLeft();
            }
            if (stack.size() == 0) {
                break;
            }
            now = stack.pop();
            now = now.getRight();
        } while (stack.size() >= 0);
    }

2. 中序遍历

 中序遍历就是从二叉树的根结点出发，当第二次到达结点时就输出结点数据，按照先向左在向右的方向访问。

从根结点出发，则第一次到达结点A，不输出A，继续向左访问，第一次访问结点B，不输出B；继续到达D，H；
到达H，H左子树为空，则返回到H，此时第二次访问H，故输出H；
H右子树为空，则返回至D，此时第二次到达D，故输出D；
由D返回至B，第二次到达B，故输出B；
按照同样规则继续访问，输出J、E、A、F、C、G；

二叉树的中序遍历输出为：
HDIBJEAFCG

中序递归遍历的思路：先递归遍历左子树，从最后一个左子树开始存入数组，然后回溯遍历双亲结点，再是右子树，这样递归循环。

非递归遍历的思路：将当前结点压入栈，然后将左子树当做当前结点，如果当前结点为空，将双亲结点取出来，将值保存进数组，然后将右子树当做当前结点，进行循环。

//递归
let result = [];
let dfs = function (node) {
     if(node) {
        dfs(node.left);
        result.push(node.value); // 直到该结点无左子树 将该结点存入结果数组 接下来并开始遍历右子树
        dfs(node.right);
    }
}
//非递归
function dfs(node) {
    let result = [];
    let stack = [];
    while(stack.length || node) { // 是 || 不是 &&
        if(node) {
            stack.push(node);
            node = node.left;
        } else {
            node = stack.pop();
            result.push(node.value);
            //node.right && stack.push(node.right);
            node = node.right; // 如果没有右子树 会再次向栈中取一个结点即双亲结点
        }
    }
    return result;
}

/*
     * 1、有左儿子，入栈 
     * 2、无左儿子，自己出栈并看右儿子是否为空 
     * 3、右儿子为空，出栈 
     * 4、右儿子不为空，入栈 
     * 5、出栈时输出
     */
    public void midIterate(TreeNode<String> root) {
        Stack<TreeNode<String>> stack = new Stack<TreeNode<String>>();
        TreeNode<String> now = root;
        do {
            while (now != null) {
                stack.push(now);
                now = now.getLeft();
            }
            if (stack.size() == 0) {
                break;
            }
            now = stack.pop();
            System.out.print(now.getData() + " ");
            now = now.getRight();
        } while (stack.size() >= 0);
    }

3. 后序遍历

 后序遍历就是从二叉树的根结点出发，当第三次到达结点时就输出结点数据，按照先向左在向右的方向访问。

从根结点出发，则第一次到达结点A，不输出A，继续向左访问，第一次访问结点B，不输出B；继续到达D，H；
到达H，H左子树为空，则返回到H，此时第二次访问H，不输出H；
H右子树为空，则返回至H，此时第三次到达H，故输出H；
由H返回至D，第二次到达D，不输出D；
继续访问至I，I左右子树均为空，故第三次访问I时，输出I；
返回至D，此时第三次到达D，故输出D；
按照同样规则继续访问，输出J、E、B、F、G、C，A；

二叉树的后序遍历输出为：
HIDJEBFGCA

后序遍历递归思路：先走左子树，当左子树没有孩子结点时，将此结点的值放入数组中，然后回溯遍历双亲结点的右结点，递归遍历。

后序遍历非递归遍历思路：先把根结点和左树推入栈，然后取出左树，再推入右树，取出，最后取根结点。

• 初始化一个栈，将根节点压入栈中，并标记为当前节点(node)；
• 当栈为非空时，执行步骤3，否则执行结束；
• 如果当前节点(node)有左子树且没有被 touched，则执行4；如果当前结点有右子树，被 touched left 但没有被 touched right 则执行5 否则执行6；
• 对当前节点(node)标记 touched left，将当前节点的左子树赋值给当前节点(node=node.left) 并将当前节点(node)压入栈中，回到3；
• 对当前节点(node)标记 touched right，将当前节点的右子树赋值给当前节点(node=node.right) 并将当前节点(node)压入栈中，回到3；
• 清理当前节点(node)的 touched 标记，弹出栈中的一个节点并访问，然后再将栈顶节点标记为当前节点(item)，回到3；

//递归
result = [];
function dfs(node) {
    if(node) {
        dfs(node.left);
        dfs(node.right);
        result.push(node.value);
    }
}
//非递归
function dfs(node) {
    let result = [];
    let stack = [];
    stack.push(node);
    while(stack.length) {
        // 不能用node.touched !== 'left' 标记‘left’做判断，
        // 因为回溯到该结点时，遍历右子树已经完成，该结点标记被更改为‘right’ 若用标记‘left’判断该if语句会一直生效导致死循环
        if(node.left && !node.touched) { // 不要写成if(node.left && node.touched !== 'left')
            // 遍历结点左子树时，对该结点做 ‘left’标记；为了子结点回溯到该（双亲）结点时，便不再访问左子树
            node.touched = 'left';
            node = node.left;
            stack.push(node);
            continue;
        }
        if(node.right && node.touched !== 'right') { // 右子树同上
            node.touched = 'right';
            node = node.right;
            stack.push(node);
            continue;
        }
        node = stack.pop(); // 该结点无左右子树时，从栈中取出一个结点，访问(并清理标记)
        node.touched && delete node.touched; // 可以不清理不影响结果 只是第二次对同一颗树再执行该后序遍历方法时，结果就会出错啦因为你对这棵树做的标记还留在这棵树上
        result.push(node.value);
        node = stack.length ? stack[stack.length - 1] : null;
        //node = stack.pop(); 这时当前结点不再从栈中取（弹出），而是不改变栈数据直接访问栈中最后一个结点
        //如果这时当前结点去栈中取（弹出）会导致回溯时当该结点左右子树都被标记过时 当前结点又变成从栈中取会漏掉对结点的访问（存入结果数组中）
    }
    return result; // 返回值
}

/*
     * 1、有儿子，入栈 
     * 2、无儿子，输出自己 
     * 3、儿子被输出过，输出自己
     */
    public void postIterate(TreeNode<String> root) {
        Stack<TreeNode<String>> stack = new Stack<TreeNode<String>>();
        TreeNode<String> now = root;
        TreeNode<String> pre = null;
        stack.push(now);
        while (stack.size() > 0) {
            now = stack.peek();
            if (now.getLeft() == null && now.getRight() == null || pre != null
                    && (now.getLeft() == pre || now.getRight() == pre)) {
                System.out.print(now.getData() + " ");
                pre = now;
                stack.pop();
            } else {
                if (now.getRight() != null) {
                    stack.push(now.getRight());
                }
                if (now.getLeft() != null) {
                    stack.push(now.getLeft());
                }
            }
        }
    }

4. 层序遍历

 层次遍历就是按照树的层次自上而下的遍历二叉树。

二叉树的层次遍历结果为：
ABCDEFGHIJ

//递归
let result = [];
let stack = [tree]; // 先将要遍历的树压入栈
let count = 0; // 用来记录执行到第一层
let bfs = function () {
    let node = stack[count];
    if(node) {
        result.push(node.value);
        if(node.left) stack.push(node.left);
        if(node.right) stack.push(node.right);
        count++;
        bfs();
    }
}
//非递归
function bfs(node) {
    let result = [];
    let queue = [];
    queue.push(node);
    let pointer = 0;
    while(pointer < queue.length) {
        let node = queue[pointer++]; // // 这里不使用 shift 方法（复杂度高），用一个指针代替
        result.push(node.value);
        node.left && queue.push(node.left);
        node.right && queue.push(node.right);
    }
    return result;
}

public class Solution {
    public ArrayList<Integer> PrintFromTopToBottom(TreeNode root) {
        ArrayList<Integer> lists=new ArrayList<Integer>();
        if(root==null)
            return lists;
        Queue<TreeNode> queue=new LinkedList<TreeNode>();
        queue.offer(root);
        while(!queue.isEmpty()){
            TreeNode tree=queue.poll();
            if(tree.left!=null)
                queue.offer(tree.left);
            if(tree.right!=null)
                queue.offer(tree.right);
            lists.add(tree.val);
        }
        return lists;
    }
}

//按照每一层输出  [[3],[9,20],[15,7]]
public List<List<Integer>> levelOrder(TreeNode root) {
        List<List<Integer>> lists=new ArrayList();
        if(root==null)
            return lists;
        levelOrderMethod(root,lists,0);
        return lists;
    }
    
    public void levelOrderMethod(TreeNode root,List<List<Integer>> lists,int level) {
        List<Integer> list=new ArrayList<Integer>();
        if (lists.size() == level)
            lists.add(list);
        lists.get(level).add(root.val);

        if(root.left!=null)
            levelOrderMethod(root.left,lists,level+1);
        if(root.right!=null)
            levelOrderMethod(root.right,lists,level+1);
    }

注：已知前序遍历序列和后序遍历序列，不可以唯一确定一棵二叉树。

本部分参考链接：https://www.jianshu.com/p/5e9ea25a1aae

七、单链表反转

1. Java实现

public static class Node {
    public int value;
    public Node next;

    public Node(int data) {
        this.value = data;
    }
}
//递归实现
public Node reverse(Node head) {
    if (head == null || head.next == null)
        return head;
    Node temp = head.next;
    Node newHead = reverse(head.next);
    temp.next = head;
    head.next = null;
    return newHead;
}
//遍历实现
public static Node reverseList(Node node) {
  Node pre = null;
  Node next = null;
  while (node != null) {
      next = node.next;
      node.next = pre;
      pre = node;
      node = next;
  }
  return pre;
}

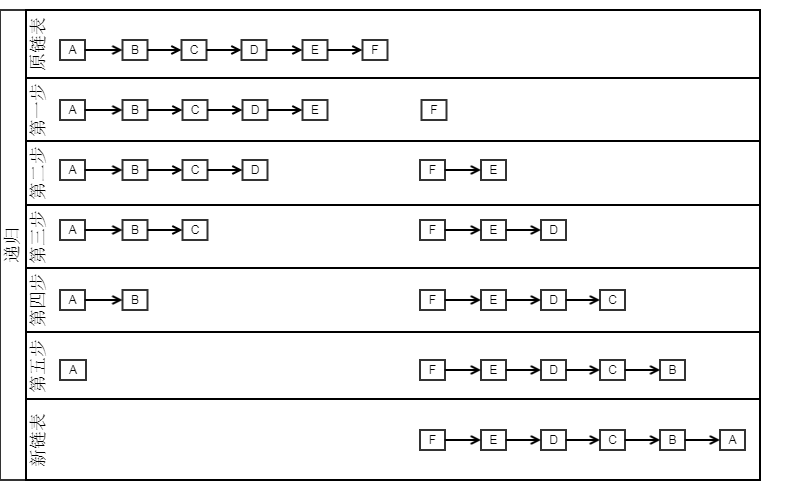
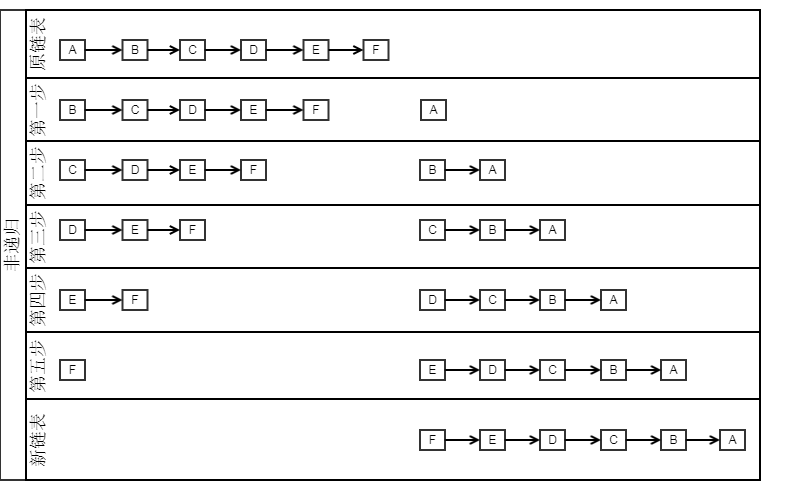
递归过程：

• 程序到达Node newHead = reverse(head.next);时进入递归
• 我们假设此时递归到了3结点，此时head=3结点，temp=3结点.next(实际上是4结点)
• 执行Node newHead = reverse(head.next);传入的head.next是4结点，返回的newHead是4结点。
• 接下来就是弹栈过程了
  • 程序继续执行 temp.next = head就相当于4->3
  • head.next = null 即把3结点指向4结点的指针断掉。

  • 返回新链表的头结点newHead。

  • 注意：当retuen后，系统会恢复2结点压栈时的现场，此时的head=2结点；temp=2结点.next(3结点)，再进行上述的操作。最后完成整个链表的翻转。 

遍历过程：

• 准备两个空结点 pre用来保存先前结点、next用来做临时变量
• 在头结点node遍历的时候此时为1结点
  • next = 1结点.next(2结点)
  • 1结点.next=pre(null)
  • pre = 1结点
  • node = 2结点
• 进行下一次循环node=2结点
  • next = 2结点.next(3结点)
  • 2结点.next=pre(1结点)=>即完成2->1
  • pre = 2结点
  • node = 3结点
• 进行循环...

本部分摘自：https://www.cnblogs.com/keeya/p/9218352.html

2. js实现

构造链表

//节点构造函数
function Node(val){
    this.val = val
    this.next = null
}
//定义链表
function List(array){
    this.head = null
    let i = 0,temp = null
    while(i < array.length){
        if( i === 0){
            this.head = new Node(array[i])
            temp = this.head
        }else{
            let newNode = new Node(array[i])
            temp.next = newNode
            temp = temp.next
        }
        i++
    }
}
//遍历链表
function traverseList(listHead){
    while(listHead){
        console.log(listHead.val)    
        listHead = listHead.next
    }
}

反转

var reverseList = function (head) {
    let pre = null
    while (head) {
        next = head.next
        head.next = pre
        pre = head
        head = next
    }
    return pre
};

八、取1000个数字里面的质数

function getNum(min,max) {
    //求范围内的所有质数
    var array=new Array();
    //判断是否是质数
    for(var i=min; i=max;i++){
        var isPrime=true;
        for(var j=2;j<i;j++){
            //被2或其他小于它的数字整除就不是质数
            if(i%j==0){
                isPrime=false;
                break;
            }
        }
    if (isPrime){
        //true代表是质数
        //向数组中添加这个数字
        array.push(i);
    }
   }
return array;
}        

 

九、找出数组中和为给定值的两个元素，如：[1, 2, 3, 4, 5]中找出和为6的两个元素。

1. 暴力法

直接遍历两次数组，时间复杂度为O(N*N)

function sameSum(arr, num){
        for (var i =0 ;i<arr.length;i++){
            for (var j = i+1;j<arr.length;j++){
                if (arr[i]+arr[j]==num){
                    console.log('数组中两个元素和为'+num+'的两个数为：'+arr[i]+'和'+arr[j]);
                    break;
                }
                //break;
                //如果只要输出一组这样的组合就只要在内层循环里break就可以
            }
        }
    }
    var arr =[1,2,3,4];
    sameSum(arr,5);
    //数组中两个元素和为5的两个数为：1和4
    //数组中两个元素和为5的两个数为：2和3

 

2. 降低复杂度

先将整型数组排序，排序之后定义两个指针left和right。left指向已排序数组中的第一个元素，right指向已排序数组中的最后一个元素，将 arr[left]+arr[right]与 给定的元素比较，若前者大，right–；若前者小，left++；若相等，则找到了一对整数之和为指定值的元素。此方法采用了排序，排序的时间复杂度为O(NlogN)，排序之后扫描整个数组求和比较的时间复杂度为O(N)。故总的时间复杂度为O(NlogN)，空间复杂度为O(1)。

//先将乱序数组排好序
    function bubbleSort(arr){
        var leng = arr.length;
        for(var i =0 ;i<leng;i++){
            for(var j =0;j<leng-i-1;j++){
                if(arr[j]>=arr[j+1]){
                    var temp = arr[j];
                    arr[j] = arr[j+1];
                    arr[j+1] = temp;
                }
            }
        }
        return arr;
    }
    //降低复杂度的方法
    function sameSum(array, num)
    {
        var newArr = bubbleSort(array);
        if(newArr == '' || newArr.length == 0){
            return false;
        }

        var left = 0, right = newArr.length -1;

        while(left < right){
            if(newArr[left] + newArr[right] > num){
                right--;
            }
            else if(newArr[left] + newArr[right] < num){
                left++;
            }
            else{
               console.log('数组中两个元素和为'+num+'的两个数为：'+newArr[left]+'和'+newArr[right]);
                left++;
                right--;
            }
        }
    }
    var arr1 = [2,1,4,3,5];
    sameSum(arr1,6);//1 + 5 = 6  2 + 4 = 6

 

十、线性顺序存储结构和链式存储结构有什么区别？以及优缺点

链表存储结构的内存地址不一定是连续的，但顺序存储结构的内存地址一定是连续的；
链式存储适用于在较频繁地插入、删除、更新元素时，而顺序存储结构适用于频繁查询时使用。

顺序存储结构和链式存储结构的优缺点：

空间上

顺序比链式节约空间。是因为链式结构每一个节点都有一个指针存储域。

存储操作上：

顺序支持随机存取，方便操作

插入和删除上：

链式的要比顺序的方便（因为插入的话顺序表也很方便，问题是顺序表的插入要执行更大的空间复杂度，包括一个从表头索引以及索引后的元素后移，而链表是索引后，插入就完成了）
例如：当你在字典中查询一个字母j的时候，你可以选择两种方式，第一，顺序查询，从第一页依次查找直到查询到j。第二，索引查询，从字典的索引中，直接查出j的页数，直接找页数，或许是比顺序查询最快的。

十一、图

1. 概念

一个图就是一些顶点的集合，这些顶点通过一系列边结对（连接）。顶点用圆圈表示，边就是这些圆圈之间的连线。顶点之间通过边连接。

（1）图是由顶点集合以及顶点间的关系集合组成的一种数据结构。

　　Graph = (V,E)  V是顶点的又穷非空集合；E是顶点之间关系的有穷集合，也叫边集合。

（2）有向图：顶点对<x,y>是有序的；无向图：顶点对<x,y>是无序的。

（3）无向边：若顶点Vi到Vj之间的边没有方向，则称这条边为无向边，用无序偶对(Vi,Vj)来表示。

　　如果图中任意两个顶点时间的边都是无向边，则称该图为无向图

（4）完全无向图：若有n个顶点的无向图有n(n-1)/2 条边, 则此图为完全无向图。

　　完全有向图：有n个顶点的有向图有n(n-1)条边, 则此图为完全有向图。

（5）树中根节点到任意节点的路径是唯一的，但是图中顶点与顶点之间的路径却不是唯一的。

　　路径的长度是路径上的边或弧的数目。

（6）如果对于图中任意两个顶点都是连通的，则成G是连通图。

（7）图按照边或弧的多少分稀疏图和稠密图。 如果任意两个顶点之间都存在边叫完全图，有向的叫有向图。

　　 若无重复的边或顶点到自身的边则叫简单图。

（8）图中顶点之间有邻接点。无向图顶点的边数叫做度。有向图顶点分为入度和出度。

（9）图上的边和弧上带权则称为网。

（10）有向的连通图称为强连通图。

2. 存储结构

邻接列表：在邻接列表实现中，每一个顶点会存储一个从它这里开始的边的列表。比如，如果顶点A 有一条边到B、C和D，那么A的列表中会有3条边

邻接列表只描述了指向外部的边。A 有一条边到B，但是B没有边到A，所以 A没有出现在B的邻接列表中。查找两个顶点之间的边或者权重会比较费时，因为遍历邻接列表直到找到为止。

邻接矩阵：在邻接矩阵实现中，由行和列都表示顶点，由两个顶点所决定的矩阵对应元素表示这里两个顶点是否相连、如果相连这个值表示的是相连边的权重。例如，如果从顶点A到顶点B有一条权重为 5.6 的边，那么矩阵中第A行第B列的位置的元素值应该是5.6：

3. 图的遍历

深度优先遍历的思想类似于树的先序遍历。其遍历过程可以描述为：从图中某个顶点v出发，访问该顶点，然后依次从v的未被访问的邻接点出发继续深度优先遍历图中的其余顶点，直至图中所有与v有路径相通的顶点都被访问完为止。
假设给定图G的初始状态是所有顶点均未曾访问过，在G中任选一顶点vi 为初始出发点，则深度优先遍历可定义如下：首先访问出发点，并将其标记为已访问过，然后，依次从vi 出发遍历vi 的每一个邻接点，若vj未曾访问过，则以vj 为新的出发点继续进行深度优先遍历，直至图中所有和vi有路径相通的顶点都被访问到为止。因此，若G是连通图，则从初始出发点开始的遍历过程结束，也就意味着完成了对图G的遍历。

连通图的深度优先遍历递归算法可描述为：
（1）访问顶点vi并标记顶点vi为已访问；
（2）查找顶点v的第一个邻接顶点vj；
（3）若顶点v的邻接顶点vj存在，则继续执行，否则算法结束；
（4）若顶点vj尚未被访问，则深度优先遍历递归访问顶点vj；
（5）查找顶点vi的邻接顶点vj的下一个邻接顶点，转到步骤（3）。
 当寻找顶点vi的邻接顶点vj成功时继续进行，当寻找顶点vi的邻接顶点vj失败时回溯到上一次递归调用的地方继续进行。为了在遍历过程中便于区分顶点是否被访问，需附设访问标志数组visited[ ]，其初值为0，一旦某个顶点被访问，则其相应的分量置为1。

广度优先遍历算法是一个分层遍历的过程，和树的层序遍历算法类同，是从图的某一顶点V0出发，访问此顶点后，依次访问V0的各个未曾访问过的邻接点；然后分别从这些邻接点出发，直至图中所有已被访问的顶点的邻接点都被访问到；若此时图中尚有顶点未被访问，则另选图中一个未被访问的顶点作起点，重复上述过程，直至图中所有顶点都被访问为止。

图的广度优先遍历算法需要一个队列以保持访问过的顶点的顺序，以便按顺序访问这些顶点邻接顶点。

连通图的广度优先遍历算法为：
（1）访问初始顶点v并标记顶点v为已访问；
（2）顶点v入队列；
（3）当队列非空时则继续执行，否则算法结束；
（4）出队列取得队头顶点u；
（5）查找顶点u的第一个邻接顶点w；
（6）若顶点u的邻接顶点w不存在，则转到步骤（3），否则执行后序语句：

• 若顶点w尚未被访问，则访问顶点w并标记顶点w为已访问；
• 顶点w入队列；
• 查找顶点u的邻接顶点w后的下一个邻接顶点，转到步骤（6）。

import java.util.*;

/**
 * 使用邻接矩阵实现图<p>
 * 深度优先遍历与广度优先遍历<p>
 * 求最短路径:<p>
 *      1. Dijkstra 算法 <p>
 *      2. Ford 算法 <p>
 *      3. 通用型的纠正标记算法<p>
 * Created by Henvealf on 16-5-22.
 */
public class Graph<T> {
    private int[][] racs;       //邻接矩阵
    private T[] verticeInfo;   //各个点所携带的信息.

    private int verticeNum;             //节点的数目,
    private int[] visitedCount;         //记录访问
    private int[] currDist;             //最短路径算法中用来记录每个节点的当前路径长度.

    public Graph(int[][] racs, T[] verticeInfo){
        if(racs.length != racs[0].length){
            throw new IllegalArgumentException("racs is not a adjacency matrix!");
        }
        if(racs.length != verticeInfo.length ){
            throw new IllegalArgumentException ("Argument of 2 verticeInfo's length is error!");
        }
        this.racs = racs;
        this.verticeInfo = verticeInfo;
        verticeNum = racs.length;
        visitedCount = new int[verticeNum];
    }

    /**
     * 深度遍历的递归
     * @param begin  从第几个节点开始遍历
     */
    public void DFS(int begin, Queue<T> edges){
        visitedCount[begin] = 1;                         //标记begin为已访问
        edges.offer(verticeInfo[begin]);                 //加入记录队列
        for(int a = 0; a < verticeNum; a++){             //遍历相邻的点
            if((racs[begin][a] != Integer.MAX_VALUE)&& visitedCount[a] == 0){   //相邻的点未被访问过
                DFS(a,edges);
            }
        }
    }

    /**
     * 开始深度优先遍历
     * @return  返回保持有遍历之后的顺序的队列
     */
    public Queue<T> depthFirstSearch(){
        initVisitedCount();         //将记录访问次序的数组初始化为0
        Queue<T> edges = new LinkedList<>();    //用于存储遍历过的点,用于输出
        int begin = -1;
        while((begin = findNotVisited()) != -1){        //不等于-1说明还有未访问过的点
            DFS(begin,edges);
        }
        return edges;
    }

    /**
     * 广度优先遍历
     * @return  返回保持有遍历之后的顺序的队列
     */
    public Queue<T> breadthFirstSearch(){
        initVisitedCount();                          //将记录访问次序的数组初始化为0
        Queue<Integer> tallyQueue = new LinkedList<>();             //初始化队列
        Queue<T> edges = new LinkedList<>();    //用于存储遍历过的点,用于输出
        int nowVertice = -1;                         //当前所在的点
        while((nowVertice = findNotVisited()) != -1){   //寻找还未被访过问的点
            visitedCount[nowVertice] = 1;             //设置访问标记
            edges.offer(verticeInfo[nowVertice]);
            tallyQueue.offer(nowVertice);               //将当前孤立部分一个顶点加入记录队列中
            while(!tallyQueue.isEmpty()){                           //只要队列不为空
                nowVertice = tallyQueue.poll();                     //取出队首的节点
                for(int a = 0; a < verticeNum; a++){     //遍历所有和nowVertice相邻的节点
                    if((racs[nowVertice][a] != Integer.MAX_VALUE) && visitedCount[a] == 0) {                      //没有访问过
                        visitedCount[a] = 1;                        //记为标记过
                        tallyQueue.offer(a);                        //加入队列,上面会继续取出.来遍历
                        edges.offer(verticeInfo[a]);                      //记录
                    }
                }
            }
        }
        return edges;
    }

    /**
     * 寻找没有被访问过的顶点.
     * @return > 0 即为还未被访问过的顶点.   -1 说明所有的节点都被访问过了.
     */
    private int findNotVisited(){
        for(int i = 0; i < verticeNum; i ++){
            if(visitedCount[i] == 0){
                return i;
            }
        }
        return -1;
    }

    /**
     * 将记录访问的数组初始化为0
     */
    private void initVisitedCount(){
        for(int i = 0; i < visitedCount.length; i ++){
            visitedCount[i] = 0;
        }
    }
}

后续遇到问题会继续补充······