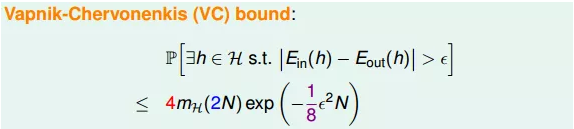《机器学习基石》第6节课学习笔记

第6节课  Theory  of  Generalization

• 上节课主要讨论了当M的数值大小对机器学习的影响，验证了M有限，最好是按照多项式成长，重点和难点是成长函数与突破点。本节课是在此基础上学习了归纳理论，引用了上限函数进行了一系列证明和推论。主要学习了只要存在break point，那么其成长函数mH(N)就满足poly(N)。推导过程是先引入mH(N)的上限B(N,k)，B(N,k)的上限是N的k-1阶多项式，从而得到mH(N)的上限就是N的k-1阶多项式。然后通过简单的三步证明，将mH(N)代入了Hoffding不等式中，推导出了Vapnik-Chervonenkis(VC) bound。（推导出VC这个公式的过程没有学好，需要补习）。

（一）回顾成长函数和突破点

1.成长函数和突破点

下图是四种常见的成长函数以及对应的突破点（有对应的图例××○○来解释）

补充：（防止忘掉成长函数和突破点的定义）

• 成长函数：数据规模为N时，可能的dichotomy的数量，记为m(N)。
• 突破点：对于某种假设空间H，如果m(k)<2^k，则k是它的突破点。

2.突破点的举例（shatter：破坏，使散开；dichotomies：二分类，二分法）

该例子推导了当最小突破点k=2时的maximum possible各种情况（因为点数量的不同而不同）

（1）当N=1和N=2时，如下图：

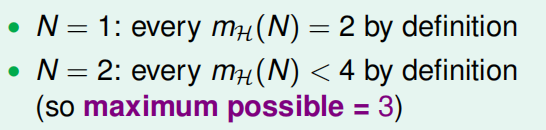
（2）当N=3时的maximum possible是多少，具体推导如下：（这部分好好理解）

①一种dichotomy时，没有出现shatter：

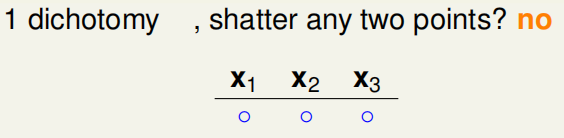
②两种dichotomy时，没有出现shatter：

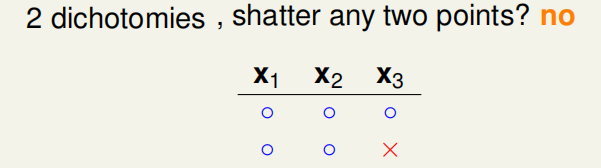
③三种dichotomy时，没有出现shatter：

④四种dichotomy时，仍存在没有出现shatter的情况：

⑤四种dichotomy时，出现shatter：

 

     

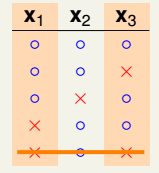
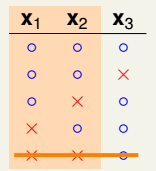
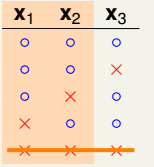
（3）结论：综上，得到的结论是列举4种情况，在3个点上任意2个点都不能shatter。即在设定的条件下，最多出现4种dichotomies。如下图：

    

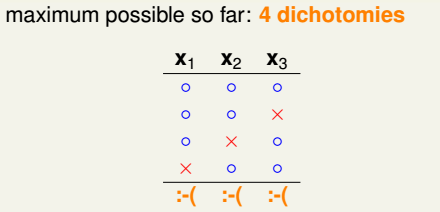
所以，我们发现当N>k时，break point限制了mH(N)值的大小，也就是说影响成长函数mH(N)的因素主要有两个：

• 抽样数据集N

• break point k（这个变量确定了假设的类型）

那么，如果给定N和k，能够证明其mH(N)的最大值的上界是多项式的，则根据霍夫丁不等式，就能用mH(N)代替M，得到机器学习是可行的。所以，证明mH(N)的上界是poly(N)，是我们的目标。

3.例题：更好的理解突破点这个例子。

 

解析：本题的意思是在3个点中任意1个点都不能shatter，问得到的最大可能性的情况（the maximum possible）是多少。经过分析答案是1。

（二）学习上限函数

1.上限函数的概念：当break point为k的时候，成长函数mH(N)可能的最大值。也就是说B(N,k)是mH(N)的上界，对应mH(N)最多有多少种dichotomy。

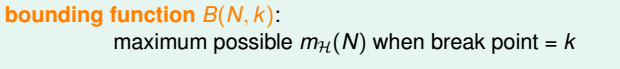
注：B(N,k)的引入只关心成长函数的上界是多少，从而简化了问题的复杂度。因此新的目标就是证明：

2.上限函数的几条性质以及对应的表格的推导：

（1）性质一：

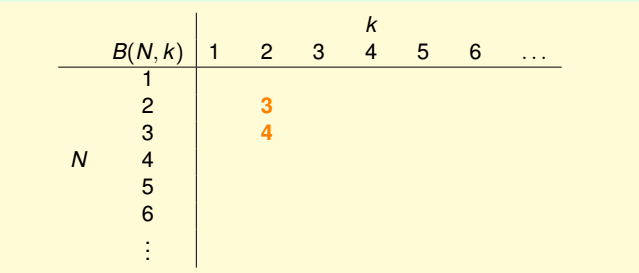
（2）性质二：

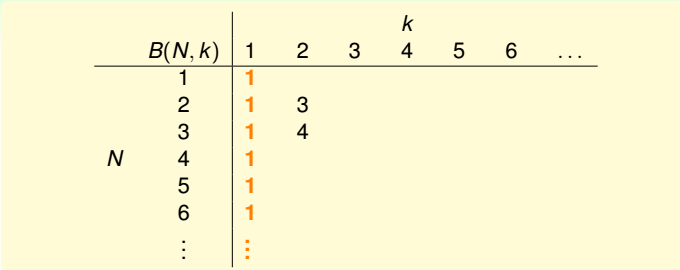
（3）性质三：

（4）性质四：

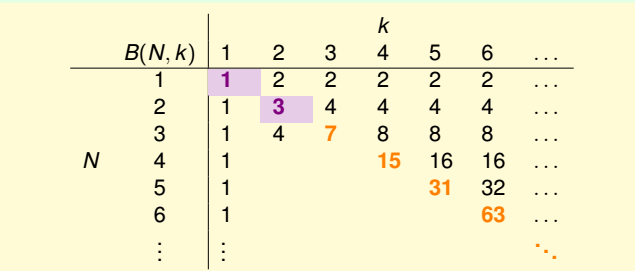
3.例题：更好的理解上限函数。

解析：上限函数是成长函数的上限，不一定有等号发生。

（三）学习上限的上限

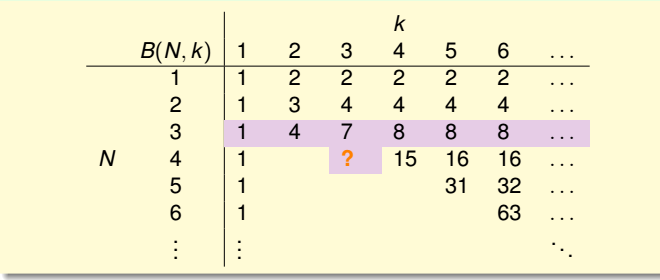
1.上限函数表的剩余部分的推导（即N>k的部分）。

（1）推导B（4,3）。

①把B(4,3)所有情况写下来，共有11组。也就是说再加一种dichotomy，任意三点都能被shattered，11是极限。

      

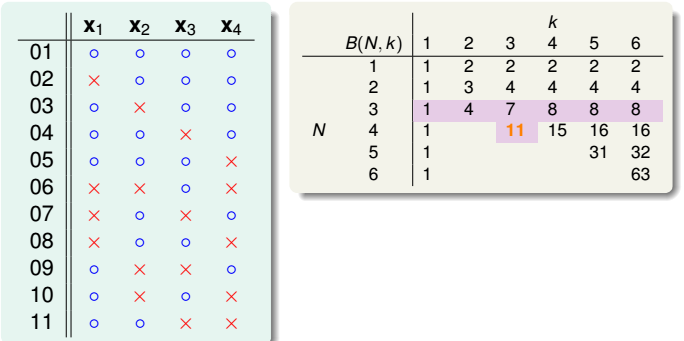
②对这11种dichotomy分组，目前分成两组，分别是orange和purple，orange的特点是，x1,x2和x3是一致的，x4不同并成对，例如1和5，2和8等，purple则是单一的，x1,x2,x3都不同，如6,7,9三组。

（2）由B（4,3）推导B（3，？）。

再以B(4,3)为例，想着能否构建B(4,3)与B(3,x)之间的关系。如下图：

   

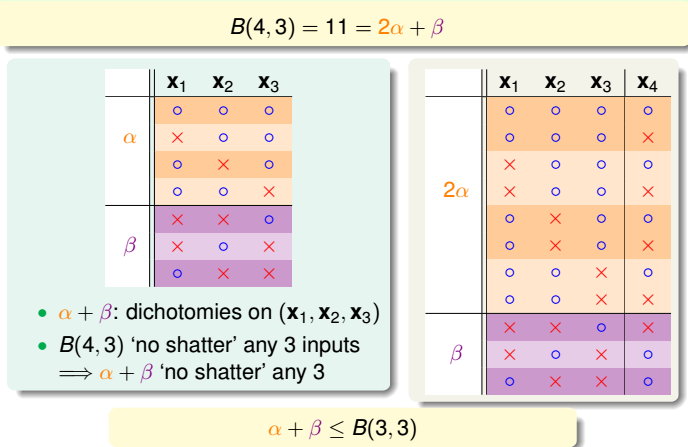
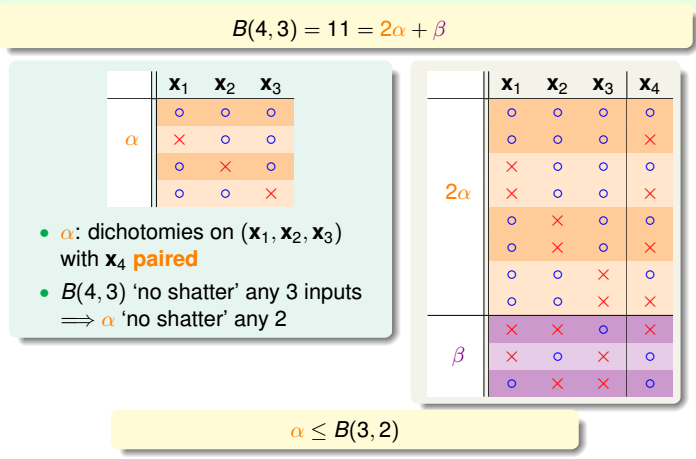
(3)最终得出的结论是（包括剩余表的填法）：

   更一般性的结论：

根据推导公式，表的剩余部分为：

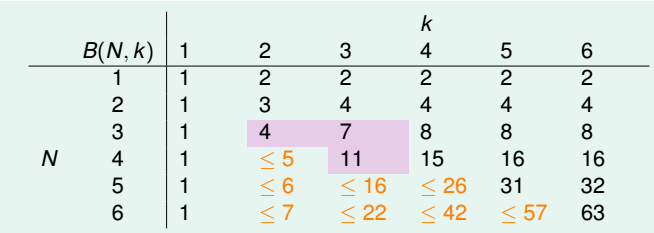
2.上限的上限（不是太理解）

根据递推公式，推导出B(N,K)满足下列不等式：

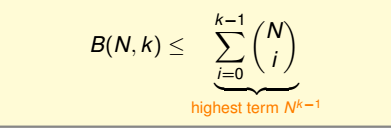
上述不等式的右边是最高阶为k-1的N多项式，也就是说成长函数mH(N)的上界B(N,K)的上界满足多项式分布poly(N)。

成长函数与上限的上限之间的关系：

结论：再次验证了成长函数的上界是poly(N)。

（四）证明了一个多项式（不太理解）

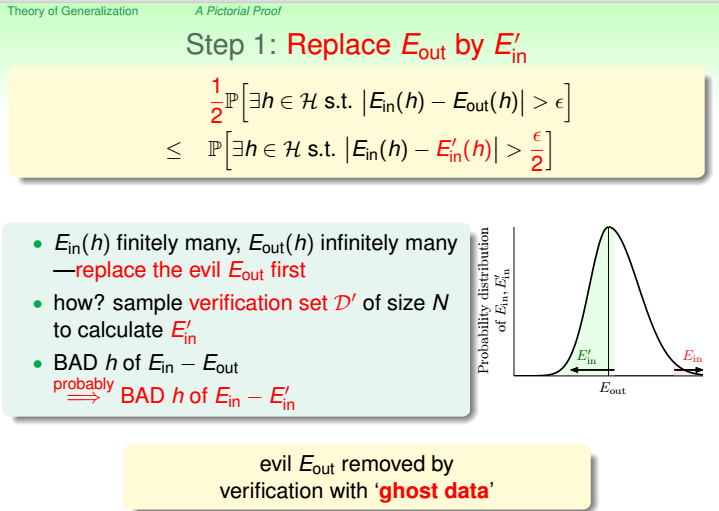
1.设想：如果能将mH(N)代替M，代入到Hoffding不等式中，就能得到Eout≈Ein的结论。

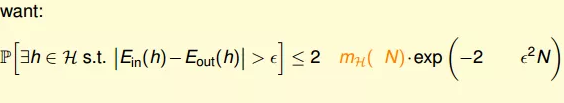
2.实际上正确的表达式为：

3.上述式子推导的3个证明过程：（只听懂了个大概）

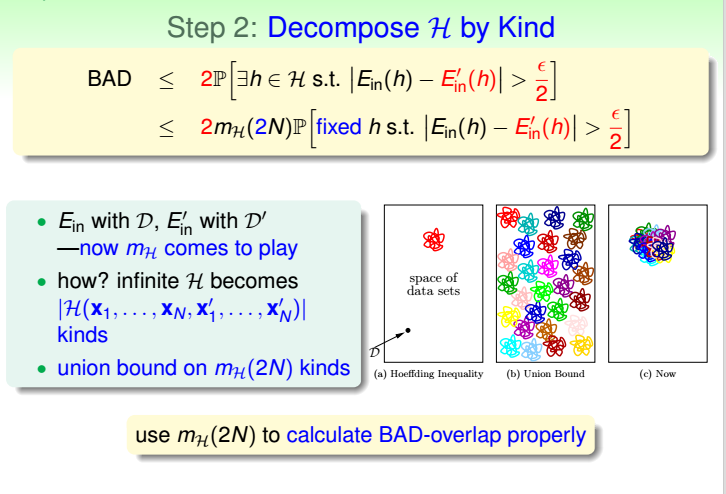
4.最终，我们通过引入成长函数mH，得到了一个新的不等式，称为Vapnik-Chervonenkis(VC) bound：