剑指offer第五章
剑指offer第五章
1.数组中出现次数超过一半的数
数组中有一个数字出现的次数超过数组长度的一半,请找出这个数字。
例如输入一个长度为9的数组{1,2,3,2,2,2,5,4,2}。由于数字2在数组中出现了5次,超过数组长度的一半,因此输出2。如果不存在则输出0。
分析:
思路1:数组排序,排序之后中间的数字一定是出现次数超过数组长度一半的数字,也就是统计学上的中位数,即长度为n的数组中第n/2大的数字(数组中任意第k大的数字)
1 class Solution { 2 public: 3 int MoreThanHalfNum_Solution(vector<int> numbers) 4 { 5 int length=numbers.size(); 6 int ans=0; 7 if(numbers.empty()) 8 return 0; 9 sort(numbers.begin(),numbers.end());//排序 10 int midNum=numbers[length/2]; 11 12 int count=0;//统计次数初始化 13 for(int i=0;i<length;i++) 14 { 15 if(numbers[i]==midNum) 16 ++count;//次数统计 17 } 18 if(count>length/2)//进行判断,是否为要求 19 ans=midNum; 20 return ans; 21 } 22 };
思路二:如果有符合条件的数字,则它出现的次数比其他所有数字出现的次数和还要多。
在遍历数组时保存两个值:一是数组中一个数字,一是次数。遍历下一个数字时,若它与之前保存的数字相同,则次数加1,否则次数减1;若次数为0,则保存下一个数字,并将次数置为1。遍历结束后,所保存的数字即为所求。然后再判断它是否符合条件即可。
1 class Solution { 2 public: 3 int MoreThanHalfNum_Solution(vector<int> numbers) 4 { 5 if(numbers.empty()) return 0; 6 7 // 遍历每个元素,并记录次数;若与前一个元素相同,则次数加1,否则次数减1 8 int result = numbers[0]; 9 int times = 1; // 次数 10 11 for(int i=1;i<numbers.size();++i) 12 { 13 if(times == 0) 14 { 15 // 更新result的值为当前元素,并置次数为1 16 result = numbers[i]; 17 times = 1; 18 } 19 else if(numbers[i] == result) 20 { 21 ++times; // 相同则加1 22 } 23 else 24 { 25 --times; // 不同则减1 26 } 27 } 28 29 // 判断result是否符合条件,即出现次数大于数组长度的一半 30 times = 0; 31 for(int i=0;i<numbers.size();++i) 32 { 33 if(numbers[i] == result) ++times; 34 } 35 36 return (times > numbers.size()/2) ? result : 0; 37 }
2.最小的k个数
输入n个整数,找出其中最小的K个数。例如输入4,5,1,6,2,7,3,8这8个数字,则最小的4个数字是1,2,3,4,。
分析:最简单的思路:把输入的n个整数排序,取最前面的k个数,时间复杂度O(nlogn)
1 class Solution { 2 public: 3 vector<int> GetLeastNumbers_Solution(vector<int> input, int k) 4 { 5 int length=input.size(); 6 vector<int> ans; 7 if(input.empty()||k>length) 8 return ans; 9 sort(input.begin(),input.end()); 10 for(int i=0;i<k;i++) 11 ans.push_back(input[i]); 12 return ans; 13 } 14 };
3.连续子数组的最大和
HZ偶尔会拿些专业问题来忽悠那些非计算机专业的同学。今天测试组开完会后,他又发话了:在古老的一维模式识别中,常常需要计算连续子向量的最大和,当向量全为正数的时候,问题很好解决。但是,如果向量中包含负数,是否应该包含某个负数,并期望旁边的正数会弥补它呢?例如:
{6,-3,-2,7,-15,1,2,2},连续子向量的最大和为8(从第0个开始,到第3个为止)。你会不会被他忽悠住?(子向量的长度至少是1) 分析:最直观的方法,即枚举出数组的所有子数组并求出他们的和。一个长度为n的数组,总共有n(n+1)/2个子数组,最快也需要O(n^2),时间复杂度比较高
代码采用下图所示方法:
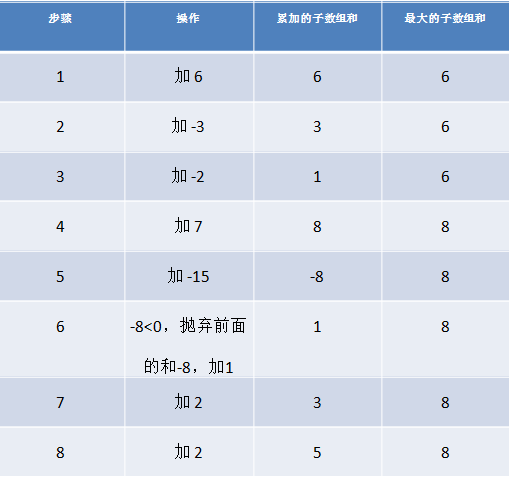
1 class Solution { 2 public: 3 int FindGreatestSumOfSubArray(vector<int> array) 4 { 5 if (array.empty()) 6 return 0; 7 int temp1 = array[0], max = array[0]; 8 for (int i = 1; i < array.size(); i++) 9 { 10 if (temp1 + array[i] > array[i]) 11 temp1 += array[i]; 12 else 13 temp1 = array[i]; 14 if (temp1 > max) 15 max = temp1; 16 } 17 return max; 18 19 } 20 };
4.从1到n整数1出现的次数
求出1~13的整数中1出现的次数,并算出100~1300的整数中1出现的次数?为此他特别数了一下1~13中包含1的数字有1、10、11、12、13因此共出现6次,但是对于后面问题他就没辙了。
希望你们帮帮他,并把问题更加普遍化,可以很快的求出任意非负整数区间中1出现的次数。
分析:最直观的方法,就是累加1到n中每个整数1出现的次数。可以每次通过对10求余数判断整数的各位数字是不是1.如果这个数字大于10,除以10之后再判断各位数字是不是1
1 class Solution { 2 public: 3 int numberOf1(int n) 4 { 5 int number=0; 6 while(n) 7 { 8 if(n%10==1) 9 { 10 number++; 11 } 12 n=n/10; 13 } 14 return number; 15 } 16 int NumberOf1Between1AndN_Solution(int n) 17 { 18 int number=0;//参数初始化 19 for(int i=1;i<=n;++i) 20 number+=numberOf1(i); 21 return number; 22 } 23 };
5.把数组排成最小的数
输入一个正整数数组,把数组里所有数字拼接起来排成一个数,打印能拼接出的所有数字中最小的一个。例如输入数组{3,32,321},则打印出这三个数字能排成的最小数字为321323。
分析:先将整型数组转换成String数组,然后将String数组排序,最后将排好序的字符串数组拼接出来。关键就是制定排序规则。
对vector容器内的数据进行排序,按照 将a和b转为string后若 a+b<b+a a排在在前 的规则排序, 如 2 21 因为 212 < 221 所以 排序后为 21 2 to_string() 可以将int 转化为string
1 class Solution { 2 public: 3 static bool cmp(int a,int b){ 4 string A=""; 5 string B=""; 6 A+=to_string(a); 7 A+=to_string(b); 8 B+=to_string(b); 9 B+=to_string(a); 10 11 return A<B; 12 } 13 string PrintMinNumber(vector<int> numbers) { 14 string answer=""; 15 sort(numbers.begin(),numbers.end(),cmp); 16 for(int i=0;i<numbers.size();i++){ 17 answer+=to_string(numbers[i]); 18 } 19 return answer; 20 } 21 };
6.丑数
把只包含因子<spanlang="en-us>">2、<spanlang="en-us>">3和<spanlang="en-us>">5的数称作丑数(<spanlang="en-us>">Ugly Number)。例如<spanlang="en-us>">6、<spanlang="en-us>">8都是丑数,但<spanlang="en-us>">14不是,因为它包含因子<spanlang="en-us>">7。习惯上我们把<spanlang="en-us>">1当做是第一个丑数。求按从小到大的顺序的第<spanlang="en-us>">N个丑数。
分析:所谓一个数m是另一个数n的因子,是指n能被m整除,也就是n%m==0思路1:尴尬 牛客网超时
根据丑数的定义,丑数只能被2,3,5整除。也就是说如果一个数能被2整除,我们把它连续除以2;如果能被3整除,连续除以3;如果能被5整除,连续除以5.如果最后得到的是1,则就是丑数
1 class Solution { 2 public: 3 bool IsUglyNumber(int number) 4 { 5 while(number%2==0) 6 number/=2; 7 while(number%3==0) 8 number/=3; 9 while(number%5==0) 10 number/=5; 11 if(number==1) 12 return true; 13 else 14 return false; 15 } 16 int GetUglyNumber_Solution(int index) 17 { 18 if(index<=0) 19 return 0; 20 int number=0; 21 int uglyFound=0; 22 while(uglyFound<index) 23 { 24 ++number; 25 if(IsUglyNumber(number)) 26 { 27 ++uglyFound; 28 } 29 } 30 return number; 31 } 32 };
思路2:创建数组保存已经找到的丑数,用空间换时间
根据丑数的定义, 丑数应该是另一个丑数乘以2、3或者5的结果(1除外) 。因此我们可以创建一个数组,里面的数字是排好序的丑数,每一个丑数都是前面的丑数乘以2、3或者5得到的。
假设数组中已经有若干个丑数排好序后放在数组中,并且把 已有最大的丑数记做M ,我们接下来分析如何生成下一个丑数。该丑数肯定是前面某一个丑数乘以2、3或者5的结果,所以我们首先考虑把已有的每个丑数乘以2。在乘以2的时候,可以得到若干个小于等于M的结果。由于是按顺序生成的,小于或者等于M肯定已经在数组中了,我们不需要再考虑;还会得到若干个大于M的结果,但我们只需要第一个大于M的结果,因为我们希望丑数是按照从小到大的顺序生成的,其他更大的结果以后再说。我们把得到的第一个乘以2后大于M的丑数记为M2。同样,我们把已有的每一个丑数乘以3和5,能得到第一个大于M的结果M3和M5。那么下一个丑数应该是M2、M3和M5这三个数的最小者了 。
前面分析的时候,提到把已有的丑数分别乘以2、3和5。事实上这不是必须的,因为已有的丑数是按照顺序放在数组中的。对乘以2而言,肯定存在某一个丑数T2,排在它之前的每一个乘以2得到的结果都会小于已有最大的丑数,在它之后的每一个丑数乘以2得到的结果都会太大。我们只需要记下这个丑数的位置,同时每次生成新的丑数的时候,取更新这个这个T2.对于乘以3和5而言,也存在着同样的T3和T5。
1 class Solution { 2 public: 3 int GetUglyNumber_Solution(int index) { 4 if(index<=0) 5 return 0; 6 int *pUglyNumber=new int[index]; 7 pUglyNumber[0]=1; 8 int NextUglyIndex=1; 9 int *pMutiply2=pUglyNumber; 10 int *pMutiply3=pUglyNumber; 11 int *pMutiply5=pUglyNumber; 12 13 while(NextUglyIndex<index) 14 { 15 int min=Min(*pMutiply2*2,*pMutiply3*3,*pMutiply5*5); 16 pUglyNumber[NextUglyIndex]=min; 17 while(*pMutiply2*2<=pUglyNumber[NextUglyIndex]) //当前最大丑数pUglyNumber[NextUglyIndex] 18 pMutiply2++; 19 while(*pMutiply3*3<=pUglyNumber[NextUglyIndex]) 20 pMutiply3++; 21 while(*pMutiply5*5<=pUglyNumber[NextUglyIndex]) 22 pMutiply5++; 23 NextUglyIndex++; 24 } 25 int ugly=pUglyNumber[index-1]; 26 delete[]pUglyNumber; 27 return ugly; 28 } 29 30 int Min(int a,int b,int c) 31 { 32 int min=a; 33 if(min>b) 34 min=b; 35 if(min>c) 36 min=c; 37 return min; 38 } 39 };
7.第一个只出现一次的字符
在一个字符串(1<=字符串长度<=10000,全部由字母组成)中找到第一个只出现一次的字符,并返回它的位置
分析:先在hash表中统计各字母出现次数,第二次扫描直接访问hash表获得次数
1 class Solution { 2 public: 3 int FirstNotRepeatingChar(string str) 4 { 5 if ( str.length() == 0) 6 return -1; 7 unsigned int hashTime[256] = {0}; 8 for(int i =0;i<str.length();++i) 9 hashTime[str[i]]++; 10 11 for(int i =0;i<str.length();++i) 12 { 13 if(hashTime[str[i]] == 1) 14 return i; 15 } 16 return -1; 17 } 18 };
8.数组中的逆序对
在数组中的两个数字,如果前面一个数字大于后面的数字,则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数P。并将P对1000000007取模的结果输出。 即输出P%1000000007
输入描述:
题目保证输入的数组中没有的相同的数字
数据范围:
对于%50的数据,size<=10^4
对于%75的数据,size<=10^5
对于%100的数据,size<=2*10^5
示例1
输入
1,2,3,4,5,6,7,0
输出
7
分析:
思路一:直接暴力 会超时
1 class Solution { 2 public: 3 int InversePairs(vector<int> d) { 4 int r = 0; 5 for(int i = 0; i < d.size(); ++i){ 6 for(int j = 0; j < i; ++j) if(d[j] > d[i]) ++r; 7 } 8 return r; 9 } 10 };
思路二:基于归并的思想
先把数组分隔成子数组,先统计出子数组内部的逆序对的数目,然后再统计出两个相邻子数组之间的逆序对的数目。在统计逆序对的过程中,还需要对数组进行排序,实际上就是归并排序。
1 class Solution { 2 public: 3 int InversePairs(vector<int> data) 4 { 5 int length=data.size(); 6 if(length<=0) 7 return 0; 8 vector<int> copy; 9 for(int i=0;i<length;i++) 10 copy.push_back(data[i]); 11 long long count=InversePairsCore(data,copy,0,length-1); 12 return count%1000000007; 13 } 14 long long InversePairsCore(vector<int> &data,vector<int> ©,int start,int end) 15 { 16 if(start==end) 17 { 18 copy[start]=data[start]; 19 return 0; 20 } 21 int length=(end-start)/2; 22 long long left=InversePairsCore(copy,data,start,start+length); 23 long long right=InversePairsCore(copy,data,start+length+1,end); 24 int i=start+length; 25 int j=end; 26 int indexcopy=end; 27 long long count=0; 28 while(i>=start&&j>=start+length+1) 29 { 30 if(data[i]>data[j]) 31 { 32 copy[indexcopy--]=data[i--]; 33 count=count+j-start-length; //count=count+j-(start+length+1)+1; 34 } 35 else 36 { 37 copy[indexcopy--]=data[j--]; 38 } 39 } 40 for(;i>=start;i--) 41 copy[indexcopy--]=data[i]; 42 for(;j>=start+length+1;j--) 43 copy[indexcopy--]=data[j]; 44 return left+right+count; 45 } 46 };
9.两个链表的第一个公共点
输入两个链表,找出他们的第一个公共结点
分析:用两个指针扫描”两个链表“,最终两个指针到达 null 或者到达公共结点。
1 /* 2 struct ListNode { 3 int val; 4 struct ListNode *next; 5 ListNode(int x) : 6 val(x), next(NULL) { 7 } 8 };*/ 9 class Solution { 10 public: 11 ListNode* FindFirstCommonNode( ListNode *pHead1, ListNode *pHead2) { 12 ListNode *p1 = pHead1; 13 ListNode *p2 = pHead2; 14 while(p1!=p2) 15 { 16 if(p1==NULL) 17 p1=pHead2; 18 else 19 p1=p1->next; 20 if(p2==NULL) 21 p2=pHead1; 22 else 23 p2=p2->next; 24 } 25 return p1; 26 } 27 };


 浙公网安备 33010602011771号
浙公网安备 33010602011771号