随机游走模型

如果你需要和图数据（Graph Data）打交道，那么你一定听说过PageRank。PageRank和其后续算法有着广泛的应用场景，包括推荐系统、反垃圾网页算法、交通规划、复杂系统故障分析等等。毫无疑问，PageRank的成功有很大一部分要归功于Google在商业上的成功。但另一方面，PageRank严谨的数学逻辑也是其备受推崇的又一重要因素。

这个关于PageRank的系列主要包括三大部分的内容：

第一大部分将详尽解释PageRank算法本身。我们采用最主流的三种方式来从不同的角度来理解PageRank，包括随机游走模型、马尔科夫链和值传播模型。

第二大部分将介绍一些关于PageRank计算、实现相关的方法，以及更复杂的数学剖析。

第三大部分将介绍一些PageRank的变种算法以及它们的应用。同时还会介绍一个PageRank的研究方向，有监督PageRank。

 朴素的随机游走模型
PageRank最早用于对网页进行“重要性”排序，它的算法逻辑可以使用随机游走模型来解释。在随机游走模型中，假设存在一个冲浪者surfer（取自“网上冲浪”的意思），在每个时刻，该surfer停留在一个网页上，并且必须从以下行动中选取一个行动：

从该网页的所有超链接中随机地选择一个链接，跳转到下一个页面；
在浏览器的地址栏中输入一个新的网址，跳转到下一个页面。我们将在后文中解释该行为。
如果一直让该surfer重复这样的选择（即每次选择一个行动，跳转到下一个页面；然后又选择一个行动，再跳转到下一个页面），并记录该surfer对每个网页的访问次数。当这样的重复次数足够大时，每个网页被访问的频率逐渐趋于稳定。这时，用频率代替概率，便得到所有网页被surfer访问的概率。这些概率就是网页的PageRank值。

上面这个模型存在两个主要问题：

如果sufer访问了一个没有超链接的页面（通常称为Dangling页面），那么他将没有办法执行行动1（他选择了行动1，但没法执行！）。这时，一种常见的做法是人为地给Dangling页面“添加”指向其它所有页面的超链接。
如果一个网页有大量链接指向网页自己，那么即使surfer选择了行动1，他仍然有很高机会停留在当前网页。为了解决该问题，一般在计算PageRank值时，网页的内部链接会被忽略掉。
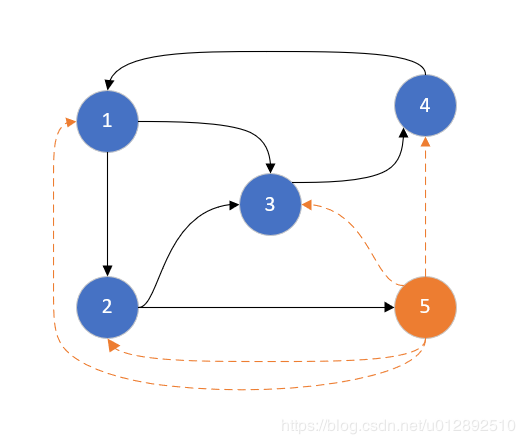
下面以一个简单的例子来描述这样的随机游走模型。