20162320刘先润队列加分项
实现循环队列
一.首先我先贴上我的循环队列代码链接。书上没有交代的方法有dequeue()、first()、isEmpty()和toString()方法
二.在实现这些方法之前,先理解书上给的enqueue()代码。
public void enqueue(T element) {
if (count == queue.length) expandCapacity();
queue[rear] = element;
rear = (rear + 1) % queue.length;
count++;
}
已知入队操作在默认空间为10的情况下,如果当空间满时则进行扩容;放入一个元素到rear队尾,如果在front队头前面有空间的情况下到达了对列最后一位,通过取余的算法将元素循环到空位,最后再使总数加1。
通过理解了教材代码,为编写后面的方法提供了思路。
三.补全操作(以下方法按难易程度有难到易排序)
- 1.第一个方法
dequeue(),我的思路是先明确指定队头元素,令队头的数组元素为null,然后,然后front+1,使队头元素成为原来队头的后一个元素,原来的队头就当做垃圾被回收,即出队。出队成功,总数count-1,经过测试代码测试,测试成功。
public T dequeue() {
T lxr = queue[front];
queue[front] = null;
front++;
count--;
return lxr;
}
- 2.第二个方法
toString(),这个方法要求将队列中每个元素都打印出来,我们可以先声明一个String变量代表它所要打印的内容,然后建立一个循环,每一次循环打印出每个组中的元素。这里我声明了两个变量a和b,我通过测试发现只声明一个a会出现漏洞,比如3个元素的队列,使用dequeue()方法去掉头后,它只会打印出第二个元素。通过排除找到原因,是因为front是随时变化的,而count也是一个变量,所以会在打印时出错,必须用两个元素声明。最后测试成功。
public String toString() {
String content = "";
for (int a=0,b =front; a < count; a++,b++) {
content += queue[b]+" ";
}
return content;
}
- 3.第三个方法 first(),虽然这个方法比较简单,但还是要注意一点,中括号内一定要用front代表第一个元素而不能用0,因为有可能出现第一个元素是空且不是队头的情况。
public T first() {
return queue[front];
}
四.测试代码,添加JUnit3测试用例,附上CircularArrayQueueTest测试代码链接和截图。

打印杨辉三角
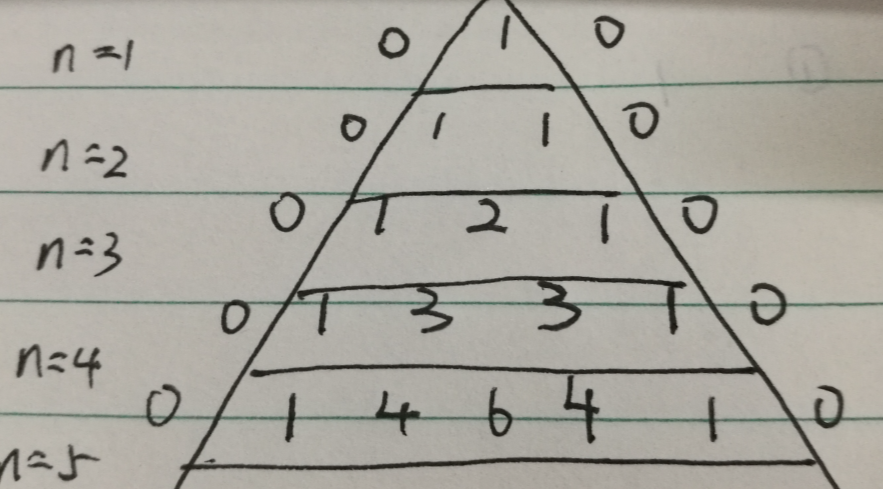
必须使用的杨辉三角基本规律
- 1.n行有n个元素
- 2.每个数等于它上方两数之和
- 3.第n行的第m个数和第n-m个数相等
设计思路:首先杨辉三角有很多规律,根据上述的可以得到一个初步的思路。比如说在第3行第1个元素1,可以由第二行的0和1相加得到。我最初的办法是建立一个循环每一次循环创建一个队列,然后排列一个算法得到每一个元素,后来通过实验发现这么做必须涉及循环内再循环,十分麻烦,而且每一行每个元素是与上一行两个元素相关的,所以这个方法被舍弃。第二个方法,建立一个队列,队列最开始放入0和1和0的第一行元素,我想通过每一个队头的元素出队都会关系到下一个入队的元素,即二者的对应关系。可以通过循环实现杨辉三角中的对角相加等于下一行某一元素这种关系。
代码执行:
- 1.用户输入显示杨辉三角的行数,保存行数值作为后面代码的变量。
System.out.println("The rows of YH Triangle are: ");
Scanner num = new Scanner(System.in);
int lines = num.nextInt();
- 2.先在队列中放入3个初始元素0、1、0,以代表第一行元素情况。设三个变量n1、n2和n3,n1表示取队头第一个元素,n2取队头的第二个元素,n3表示n1和n2之和,即杨辉三角中下一行的对应元素。建立一个内层循环,每取1次当前队头第一个元素,便让其出栈,再取一次队头第一个元素,两次结果之和便得到下一个入队的元素。如此往复每一个内层循环结束一行的杨辉三角。最后便是外层循环,调用第一步得到的行数lines,循环补全lines-1行,例如用户需求5行就循环补全第2-5行。由于我做的杨辉三角模式是从每一行横向移动到末端,所以每一次外层循环必须入队一个隐藏的元素0。
lxr.enqueue(0);
lxr.enqueue(1);
for(int rows =0;rows<lines-1;rows++){ //循环的次数
lxr.enqueue(0);
for(int i=1;i<=lxr.size()-1;i++){
int n1=lxr.first();//取第一个元素
int n2 = lxr.second();//取第二个元素
lxr.dequeue();
int n3 = n1+n2;
lxr.enqueue(n3);//得到下一个入队元素
System.out.print(n3+" ");
}
System.out.println();
}
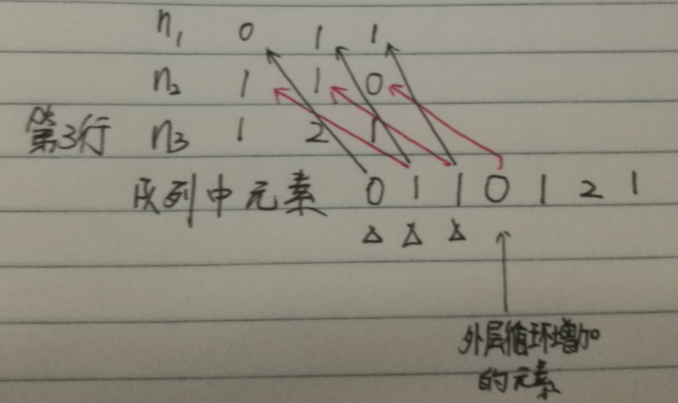
思路详解:举个例子,我要打印三行的杨辉三角,见下图是第二行的打盈印流程,队伍中最开始只有0、1、0三个元素,黑线指向代表"队伍中的哪个元素代表n1",红线指向代表“队伍中n1后面的一个元素”,而黑虚线代表“由n1相加n2得到入队的元素”,△代表从左到右依次出队的元素。通过执行这一次循环会得到杨辉三角的第二行1 1。

到了第三行,如下图所示,队伍中的元素总数(count)由3个增加到了4个,即第n行中队伍会有n+1个元素,同第二行步骤类推,最后得到打印结果1 2 1 ,因为我手动补全的第一行,所以一个三行的杨辉三角成型。
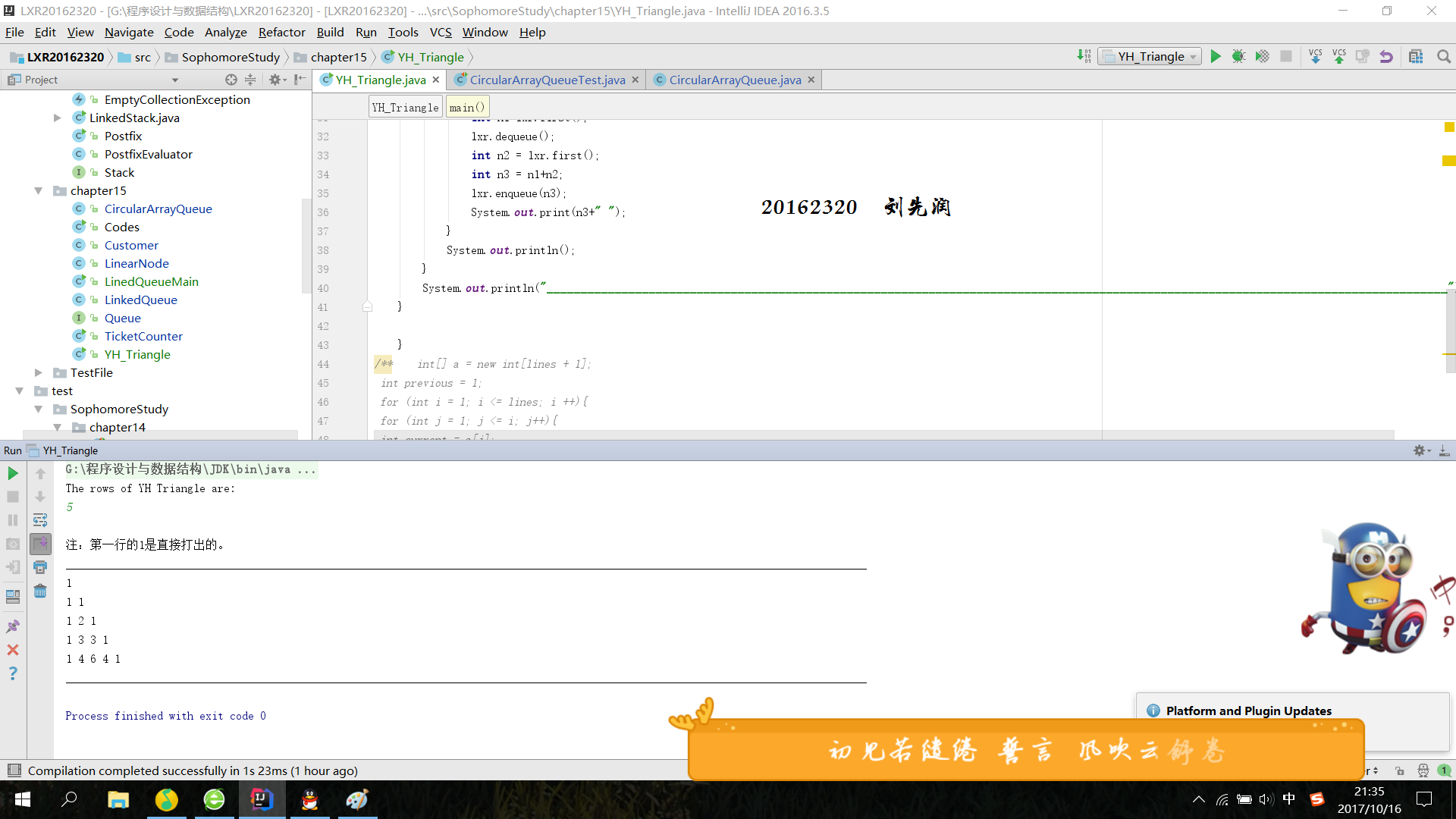
- 3.代码测试,我输入5行的杨辉三角,截图如下:
附:实验内容代码和用图和博客都出自20162320刘先润之手,如有雷同,老师懂的(_)
杨辉三角YH_Triangle代码链接
实验中的注意:
- 1.CircularArrayQueue类的最大容量一定要设计一个较高的值,我设置的就是1000,因为通过测试容量不够的话,当杨辉三角行数过多时会报错。
- 2.为了方便得出入栈的元素,我先放入了杨辉三角的第1行元素,所以行数lines需要减1。
- 3.外层循环与内层循环之间一定要入队一个0元素,才能得到后面的结果,因为杨辉三角中0元素是省略的。
- 4.为了方便杨辉三角,我在CircularArrayQueue类中添加了
second()的方法,即返回队列中队头后一位的元素。



