数据结构(天梯L2 部分题解)
L2-014 列车调度
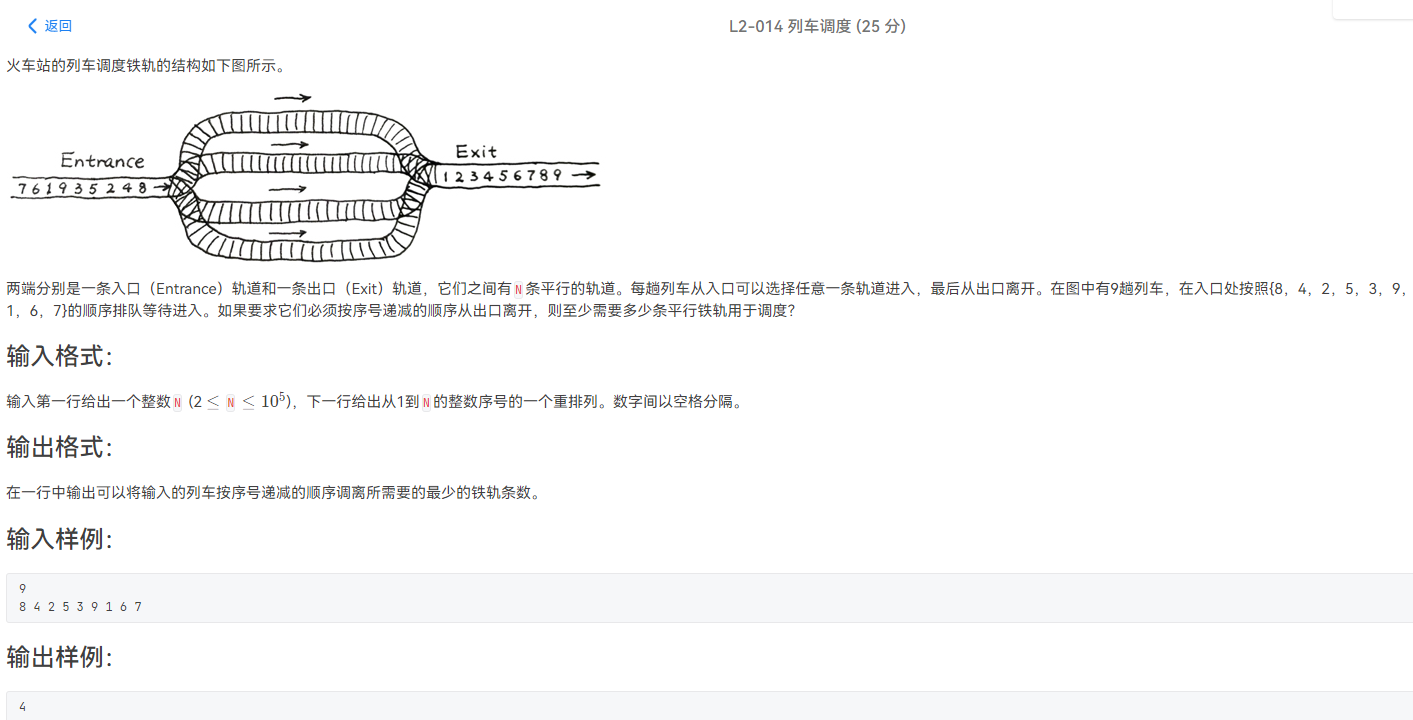
这个题的话,可以用贪心的思想,当新的火车进站时,保证这列火车一定停靠在刚刚比他大的最小的数的后面,由于数据量比较大,我们可以考虑使用二分查找来寻找符合要求的那个数即可
#include<stdio.h> int train[100100]; int a[100100]; int len=0; int erfen(int x) //二分查找模板 { int left=-1,right=len; while (left+1<right) { int mid; mid=(left+right)/2; if (train[mid]>x) { right=mid; } else { left=mid; } } return right; } int main() { int n,i; scanf("%d",&n); for (i=0;i<n;i++) { scanf("%d",&a[i]); } for (i=0;i<n;i++) { if (len==0) { train[0]=a[i]; len++; } else { int ans; ans=erfen(a[i]); // printf("%d\n",ans); int ii; // for (ii=0;ii<=len;ii++) // { // printf("%d ",train[ii]); // } // printf("\n"); if (ans>=0 && ans<len) { train[ans]=a[i]; } else { train[len]=a[i]; len++; } } } printf("%d\n",len); return 0; }
L2-012 关于堆的判断
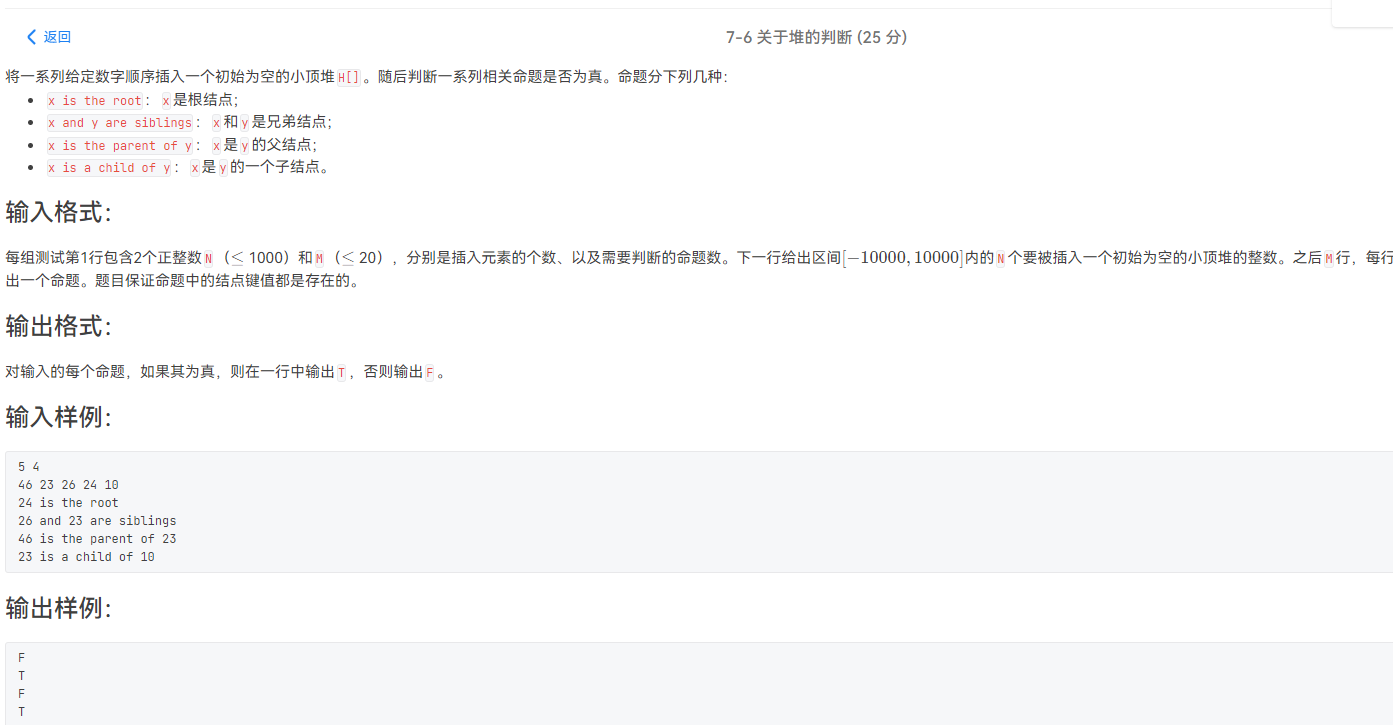
这个题有两个难点,一个是堆的概念和定义,另一个则是字符串的处理
首先,题目中所给出的小顶堆是指一种经过排序的完全二叉树,其中任一非终端节点的数据值均不大于其左子节点和右子节点的值,可以戳链接去学习一下~,根据小顶堆的定义使用数组来模拟创建整个小顶堆的过程,根据得到的数组元素下标与二叉树各个节点的关系,即可进行判断。
数据结构——小顶堆的构建,添加,删除_wenge1477的博客-CSDN博客_小顶堆的构造
堆排序(大顶堆、小顶堆)----C语言 - 蓝海人 - 博客园 (cnblogs.com)
其次是字符串的处理,特别要注意的是负数的处理哦
#include<stdio.h> #include<bits/stdc++.h> #include<string.h> using namespace std; int a[1010]; int n; void create_dui(int len) //创建小顶堆,根据定义判断一个非叶子节点的值与是否大于它的左右孩子的值,依次比较来完成建堆操作 { int i; for (i=len/2-1;i>=0;i--) { if (a[i*2+1]<a[i] && ((i*2+1)<len)) { int tmp; tmp=a[i*2+1]; a[i*2+1]=a[i]; a[i]=tmp; if (((2*(2*i+1)+1)<len && a[2*(2*i+1)+1]<a[i*2+1]) || (((2*(2*i+1)+2)<len) && a[2*(2*i+1)+2]<a[2*i+1])) { create_dui(len); } } if (a[i*2+2]<a[i] && ((i*2+2)<len)) { int tmp; tmp=a[i*2+2]; a[i*2+2]=a[i]; a[i]=tmp; if (((2*(i*2+2)+1)<len && a[2*(i*2+2)+1]<a[i*2+2]) || ((2*(i*2+2)+2)<len && a[2*(i*2+2)+2]<a[i*2+2])) { create_dui(len); } } } } int main() { int m,i; scanf("%d %d",&n,&m); for (i=0;i<n;i++) { scanf("%d",&a[i]); create_dui(i+1); } getchar(); for (i=0;i<m;i++) { char s[50]; cin.getline(s,50); int sm=strlen(s); int j=0; int miu1=0,miu2=0; int x=0,y=0; while ((s[j]>='0' && s[j]<='9' ||s[j]=='-')) { if (s[j]=='-') { miu1=1; } else { x=x*10+(s[j]-48); } j++; // printf("JX:%d %d %d\n",j,x,s[j]-48); } if (miu1==1) { x=-x; } j--; int ZJ=j; j++; //注意负数处理 while (!((s[j]>='0' && s[j]<='9') || s[j]=='-')) { if (j>=sm) { break; } j++; } while ((s[j]>='0' && s[j]<='9') || s[j]=='-') { if (s[j]=='-') { miu2=1; } else { y=y*10+(s[j]-48); } if (j>=sm) { break; } j++; } if (miu2==1) { y=-y; } j--; if (s[sm-1]=='t') { if (x==a[0]) { printf("T\n"); } else { printf("F\n"); } continue; } if (s[sm-1]=='s') { int XI,YI; int ii; for (ii=0;ii<n;ii++) { if (x==a[ii]) { XI=ii; } if (y==a[ii]) { YI=ii; } } XI++; YI++; int xt1,xt2; xt1=XI/2; xt2=YI/2; if (xt1==xt2) { printf("T\n"); } else { printf("F\n"); } continue; } if (s[ZJ+9]=='p') { int XI,YI,ii; for (ii=0;ii<n;ii++) { if (x==a[ii]) { XI=ii; } if (y==a[ii]) { YI=ii; } } YI--; if ((YI/2)==XI) { printf("T\n"); } else { printf("F\n"); } } if (s[ZJ+7]=='c') { int XI,YI,ii; for (ii=0;ii<n;ii++) { if (x==a[ii]) { XI=ii; } if (y==a[ii]) { YI=ii; } } XI--; if ((XI/2)==YI) { printf("T\n"); } else { printf("F\n"); } } } return 0; }
L2-005 集合相似度
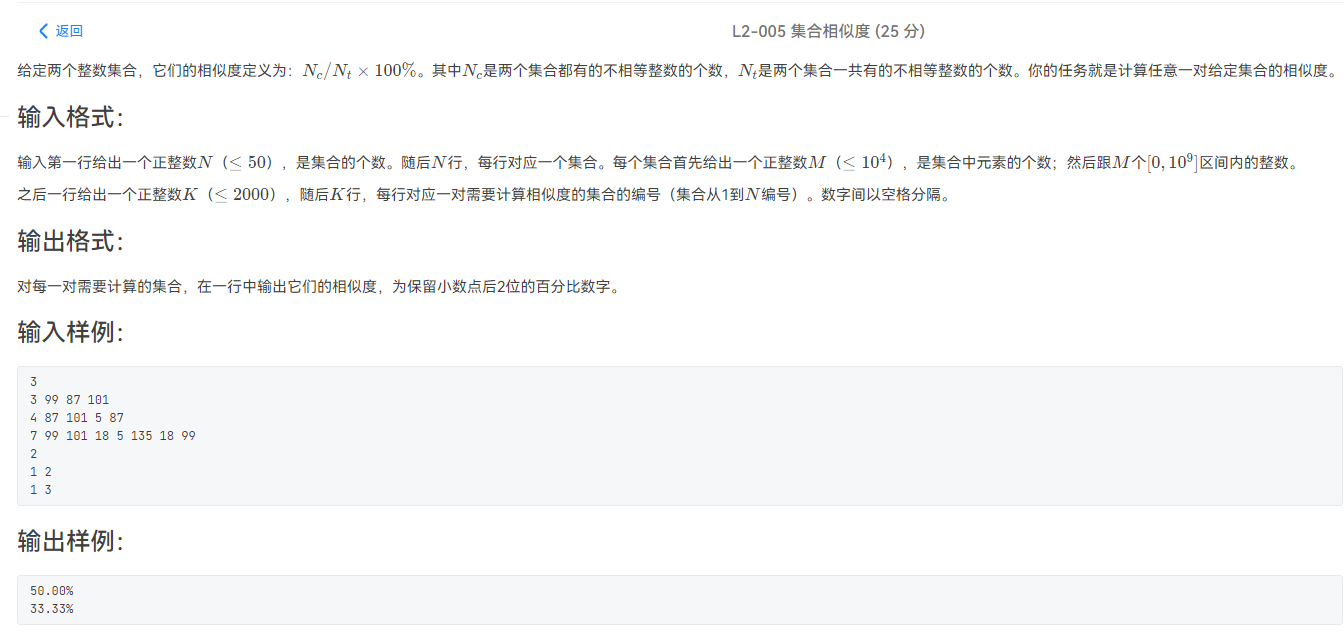
在题干中,提到了“集合”这个词,所以,我们应该使用C++STL库中的set来进行实现。set是STL中的常见容器,set中不允许重复元素,并且set中的元素是排好序的
使用set之前,要先添加头文件#include<set>,以下是以set相关的函数:
1.向set中插入元素:a.insert(x);
2.返回set中元素的个数:a.size();
3.返回set容器第一个元素的地址:a.begin();
4.返回set容器最后一个元素的地址:a.end();
5.删除set容器中的所有元素:a.clear();
6.判断set容器是否为空:a.empty();
7.判断set容器中可能包含元素的最大个数:a.max_size();
8.返回元素在集合中出现的次数:a.count(x); 由于set中元素不重复,返回值只为0或1
*set只能通过迭代器来访问
故在完成本题时,我们可以使用set来存储每个集合中的元素,之后使用set.count在集合b中寻找该集合a中的元素是否在集合b中出现,统计出两个集合里都有的元素数量,使用元素总的数量减去两个集合中都有的元素的个数,就可以得到两个集合中共有的不同元素的个数,从而方便快捷地完成这道题目。
#include<stdio.h> #include<set> #include<bits/stdc++.h> using namespace std; set <int>s[55]; int main() { int n,i,j; scanf("%d",&n); for (i=1;i<=n;i++) { int m; scanf("%d",&m); for (j=0;j<m;j++) { int z; scanf("%d",&z); s[i].insert(z); } } int k; scanf("%d",&k); for (i=0;i<k;i++) { int a,b; int cnt=0; scanf("%d %d",&a,&b); set <int> :: iterator it; for (it=s[a].begin();it!=s[a].end();it++) { if (s[b].count(*(it))) { cnt++; } } if (s[b].count(*(s[a].end()))) { cnt++; } double ans; ans=(cnt*1.0)*100/(s[a].size()+s[b].size()-cnt); printf("%.2f%%\n",ans); } return 0; }
L2-006 树的遍历
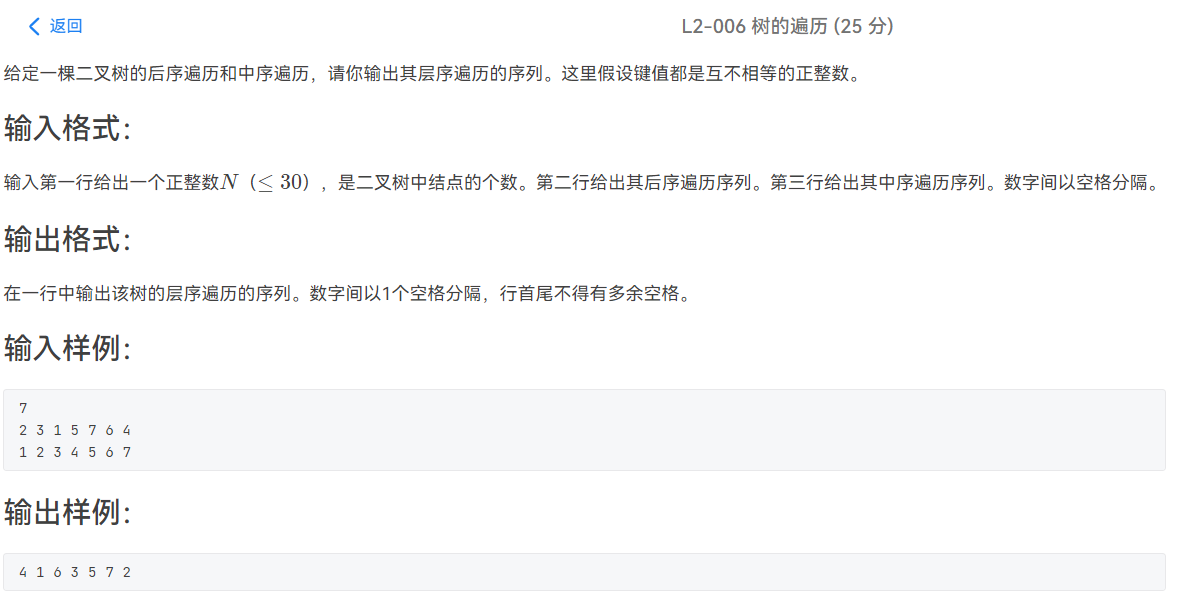
这个题的话主要偏向于二叉树的应用,主要是要熟悉二叉树的建树方法,下面是模板:
已知前序遍历和中序遍历,确定一棵二叉树:
tree *create(int h1,int t1,int h2,int t2) { // printf("__17__\n"); if (h1>t1 || h2>t2) { return NULL; } tree *root=(tree *)malloc((sizeof(tree))); root->c=s1[h1]; int i; for (i=h2;i<=t2;i++) { if (s1[h1]==s2[i]) { break; } } root->left=create(h1+1,h1-h2+i,h2,i-1); root->right=create(h1-h2+i+1,t1,i+1,t2); return root; }
已知后序遍历和中序遍历,确定一棵二叉树:
TreeNode *create_tree(int front1,int rear1,int front2,int rear2) { if (front1>rear1) { return 0; } TreeNode *root =(TreeNode *)malloc(sizeof(TreeNode)); root->data=back[rear2]; // printf("46:%d\n",root->data); root->left=NULL; root->right=NULL; int p=0; while (middle[p]!=root->data) { p++; } int num=p-front1; root->left=create_tree(front1,p-1,front2,front2+num-1); root->right=create_tree(p+1,rear1,front2+num,rear2-1); return root; }
二叉树后序遍历输出(前、中序也一样,注意递归的顺序就行):
void print(tree *TREE) { if (TREE==NULL) { return; } print(TREE->left); print(TREE->right); printf("%c",TREE->c); }
二叉树层序遍历输出:(其实就是一个BFS)
void floorprint(TreeNode *Tree) { queue <TreeNode*> q; int flag=0; q.push(Tree); while (!q.empty()) { TreeNode *s=q.front(); q.pop(); if (flag==0) { printf("%d",s->data); flag=1; } else { printf(" %d",s->data); } if (s->left!=NULL) { q.push(s->left); } if (s->right!=NULL) { q.push(s->right); } } }
题解代码如下,用模板即可:
#include<stdio.h> #include<stdlib.h> #include<string.h> #include<queue> using namespace std; int back[40],middle[40]; struct TreeNode{ int data; TreeNode *left; TreeNode *right; }Node,Tree; void floorprint(TreeNode *Tree) { queue <TreeNode*> q; int flag=0; q.push(Tree); while (!q.empty()) { TreeNode *s=q.front(); q.pop(); if (flag==0) { printf("%d",s->data); flag=1; } else { printf(" %d",s->data); } if (s->left!=NULL) { q.push(s->left); } if (s->right!=NULL) { q.push(s->right); } } } TreeNode *create_tree(int front1,int rear1,int front2,int rear2) { if (front1>rear1) { return 0; } TreeNode *root =(TreeNode *)malloc(sizeof(TreeNode)); root->data=back[rear2]; root->left=NULL; root->right=NULL; int p=0; while (middle[p]!=root->data) { p++; } int num=p-front1; root->left=create_tree(front1,p-1,front2,front2+num-1); root->right=create_tree(p+1,rear1,front2+num,rear2-1); return root; } int main() { int n,i; scanf("%d",&n); for (i=0;i<n;i++) { scanf("%d",&back[i]); } for (i=0;i<n;i++) { scanf("%d",&middle[i]); } TreeNode *root=create_tree(0,n-1,0,n-1); floorprint(root); return 0; }
L2-025 分而治之
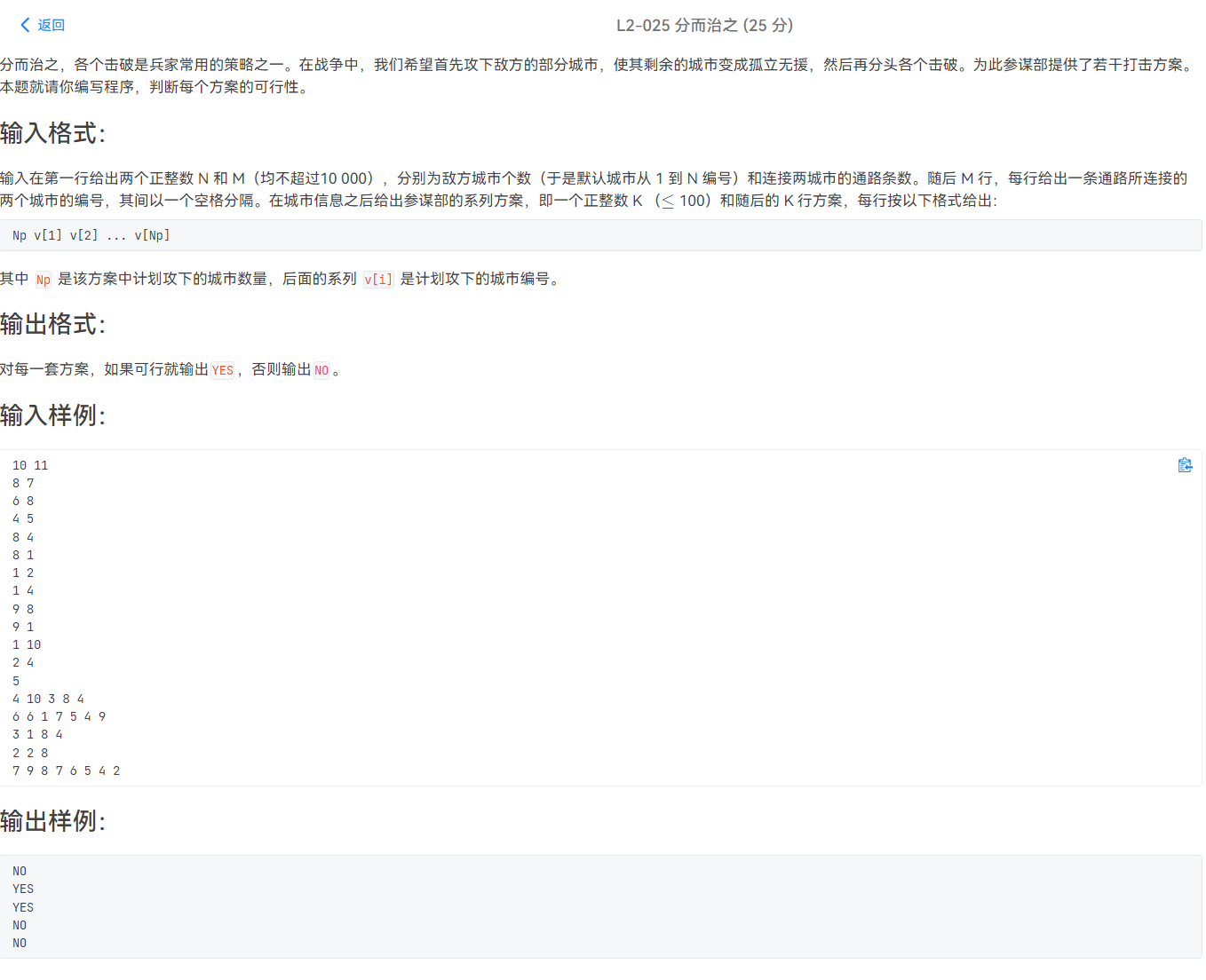
这个题的不同之处就在于城市的数量很多,用传统图论中邻接矩阵的话,会超过规定的内存,故采用邻接表来存储即可。使用邻接表来存储城市间的关系,在使用一个vis数组来表示该城市是否被占领就行。注意在使用邻接表时,由于是一个无向图,故在开表的大小的时候需要乘上2哦~。
参考代码:
#include<stdio.h> #include<string.h> struct Edge{ //构建邻接表 int nxt,to; }edge[20020]; int num_edge=0,head[10010]; bool vis[10010]={false}; void add_edge(int fr,int to) //添加边 { edge[++num_edge].nxt=head[fr]; edge[num_edge].to=to; head[fr]=num_edge; } int main() { int n,m,i; scanf("%d %d",&n,&m); for (i=0;i<m;i++) { int a,b; scanf("%d %d",&a,&b); add_edge(a,b); add_edge(b,a); } int k,ii,j; scanf("%d",&k); for (i=0;i<k;i++) { int np; scanf("%d",&np); int ans=0; memset(vis,false,sizeof(bool)*10001); for (j=0;j<np;j++) { int c; scanf("%d",&c); for (ii=head[c];ii!=0;ii=edge[ii].nxt) //遍历每一个邻接表的点 { if (vis[edge[ii].to]!=true) { ans++; } } vis[c]=true; } if (ans==m) { printf("YES\n"); } else { printf("NO\n"); } } return 0; }
*********************附图论相关模板
dijkstra算法模板:
void dijkstra(int s,int t) { int i,j; for (i=1;i<=n;i++) //初始化 { dis[i]=mp[s][i]; } for (int i=1;i<=n-1;i++) //for循环n次,找每个点的最短路 { int minn=INF,u; for (j=1;j<=n;j++) //在没有确定最短路的点中,找出距离最短的那个点 { if (book[j]==0 && dis[j]<minn) { minn=dis[j]; u=j; } } book[u]=1;//表示u这个点已经确定最短路了 for (int j=1;j<=n;j++)//用u来更新其他点的最短路 { if (dis[u]+mp[u][j]<dis[j]) { dis[j]=dis[u]+mp[u][j]; } } } if (dis[t]==INF) { printf("-1\n"); } else { printf("%d\n",dis[t]); } }
给你一副N个点M条边的有向图(点的编号是从1~N),然后有Q次询问,每次询问输入一个点的编号,按升序输出与这个点连接的所有点,对于每次询问,每个关联点只输出一次,如果没有关联点,则输出NULL。
#include<stdio.h> #include<string.h> #include<bits/stdc++.h> using namespace std; #define MAX 1000100 struct Edge{ int nxt,to; }edge[MAX]; int num_edge=0,head[10010]; int answer[1001000]={0}; void add_edge(int fr,int to) { edge[++num_edge].nxt=head[fr]; edge[num_edge].to=to; head[fr]=num_edge; } int main() { int n,m,q; while(scanf("%d %d %d",&n,&m,&q)!=EOF) { int i,j,ii; vector<int>ans; num_edge=0; memset(head,0,sizeof(int)*10010); for (i=1;i<=m;i++) { int a,b; scanf("%d %d",&a,&b); add_edge(a,b); } for (ii=0;ii<q;ii++) { int c; int flag=0; scanf("%d",&c); if (head[c]==0) { printf("NULL\n"); } else { // int T=0; // memset(answer,0,sizeof(int)*1001000); ans.clear(); for (i=head[c];i!=0;i=edge[i].nxt) { ans.push_back(edge[i].to); } sort(ans.begin(),ans.end()); ans.erase(unique(ans.begin(),ans.end()),ans.end()); for (i=0;i<(int)ans.size();i++) { printf("%d\n",ans[i]); } } } } return 0; }
链表-dijkstra
#include<bits/stdc++.h> using namespace std; typedef pair<int,int> PII; const int N=100100; int n,m,s,t; int idx,d[N]; bool st[N]; struct Edge{ int nxt,to,w; }edge[20*N]; int num_edge=0,head[N]; void add_edge(int fr,int to,int w) { edge[++num_edge].nxt=head[fr]; edge[num_edge].to=to; edge[num_edge].w=w; head[fr]=num_edge; } void dijkstra() { memset(d,0x3f,sizeof d); d[s]=0; priority_queue<PII,vector<PII>,greater<PII>> q; q.push({0,s}); while(q.size()) { auto t=q.top(); q.pop(); /* for (i=1;i<=n;++i) dis[i]=inf;//初始化起点到各点距离 */ if (st[t.second]) { continue; } st[t.second]=true; for (int i=head[t.second];~i;i=edge[i].nxt) { int j=edge[i].to; if (d[j]>max(t.first,edge[i].w)) { d[j]=max(t.first,edge[i].w); q.push({d[j],j}); } /*if(d[j>d[u]+e.cost){ d[e.to]=d[u]+e.cost; Q.push((HeadNode){d[e.to],e.to}); } */ } /*for (i=head[t.second];i!=-1;i=e[i].next) { int to=edge[i].to;//本次循环中的目标点 if (dis[to]>edge[i].w+dis[t.second]&&!vis[to]) { dis[to]=dis[t.second]+edge[i].w;//松弛 q.push({dis[to],to});//将到起点距离变短的点加入队列 } }*/ } } int main() { int i; cin>>n>>m>>s>>t; memset(head,-1,sizeof head); for (i=0;i<m;i++) { int u,v,w; scanf("%d %d %d",&u,&v,&w); add_edge(u,v,w); add_edge(v,u,w); } dijkstra(); cout<<d[t]<<endl; return 0; }



