蓝桥杯算法2016年 抽签(全排列(递归+回溯))剪邮票(全排列next_permutation()+dfs连通性检查)迷宫问题dfs()
1.抽签
1.1题目描述
本题为代码补全填空题,请将题目中给出的源代码补全,并复制到右侧代码框中,选择对应的编译语言(C/Java)后进行提交。若题目中给出的源代码语言不唯一,则只需选择其一进行补全提交即可。复制后需将源代码中填空部分的下划线删掉,填上你的答案。提交后若未能通过,除考虑填空部分出错外,还需注意是否因在复制后有改动非填空部分产生错误。
X星球要派出一个 5 人组成的观察团前往 W 星。
其中:
A 国最多可以派出 4 人。
B 国最多可以派出 2 人。
C 国最多可以派出 2 人。
....
那么最终派往 W 星的观察团会有多少种国别的不同组合呢?
下面的程序解决了这个问题。 数组 a[] 中既是每个国家可以派出的最多的名额。 程序执行结果为:
DEFFF
CEFFF
CDFFF
CDEFF
CCFFF
CCEFF
CCDFF
CCDEF
BEFFF
BDFFF
BDEFF
BCFFF
BCEFF
BCDFF
BCDEF
....
(以下省略,总共101行)下面的代码就是为了这个目的的,请仔细阅读源码,并填写划线部分缺少的代码。
源代码:
C
#include <stdio.h>
#define N 6
#define M 5
#define BUF 1024
void f(int a[], int k, int m, char b[])
{
int i,j;
if(k==N){
b[M] = 0;
if(m==0) printf("%s\n",b);
return;
}
for(i=0; i<=a[k]; i++){
for(j=0; j<i; j++) b[M-m+j] = k+'A';
______________________; //填空位置
}
}
int main()
{
int a[N] = {4,2,2,1,1,3};
char b[BUF];
f(a,0,M,b);
return 0;
}
1.2实现代码:#include <stdio.h> #define N 6 #define M 5 #define BUF 1024 /** k是a数组的下标, m是派出的人数, b是用字符串代表国家 **/ void f(int a[], int k, int m, char b[]) { int i,j; if(k==N){ //递归的终止条件,(这里可以想到k是变大的) b[M] = 0; if(m==0) printf("%s\n",b);//(这里可以知道m是变小的) return; } for(i=0; i<=a[k]; i++){//由a[k]可知i是每个国家派出的人数 for(j=0; j<i; j++) b[M-m+j] = k+'A';//派出i人,则用i个字符表示 f(a,k+1,m-i,b); //填空位置 (第k个国家派出i人后,则继续下一个国家,即k+1。剩下的5-i人继续递归,则是m-i。) } } int main() { int a[N] = {4,2,2,1,1,3}; char b[BUF]; f(a,0,M,b); return 0; }
1.3题型总结:
(1)若题目有终止条件可考虑是否为递归问题,递归问题一般填空都是f(a,k+1....)类似的。判断递归填空题,主要是要知道递归函数的参数代表什么。
(2)组合问题常用:全排列(递归+回溯)
2.剪邮票
2.1 题目描述
如【图1.jpg】, 有12张连在一起的12生肖的邮票。
现在你要从中剪下 55 张来,要求必须是连着的。
(仅仅连接一个角不算相连) 比如,【图2.jpg】,【图3.jpg】中,粉红色所示部分就是合格的剪取。
请你计算,一共有多少种不同的剪取方法。
2.2 解决思路
(1)题型分析:这种问题是在几个数中选若干个数,然后咋滴咋滴。像这种问题也是属于组合问题,我们可以用全排列+check(),只不过这里要检测连通性,说到连通性我们肯定会想到要使用dfs()要检测,所以最终选择使用全排列+dfs()+check()。
(2)思路分析:在12个数里面选5个数,然后看是否连通。我们可以把这12个数用0,1表示,1代表要选择的数,如下:
int a[12] = {0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1};
然后进行全排列,就可以随机的选到五个数啦,然后我们再把一维数组a转化成上图中的二维数组,如下:
//将a变成二维矩阵的形式 int g[3][4]; for (int i = 0; i < 3; i++) { for (int j = 0; j < 4; j++) { g[i][j] = a[i * 4 + j]; } }
转成二维数组之后,再一个个的check(),如果是1就进行dfs深入检查是否连通,检查这个图中有几个连通块,直到检查到最后一个为止,如下:
//对g上的每一点进行连通性检查 int cnt = 0;//连通块的数目 for (int i = 0; i < 3; i++) { for (int j = 0; j < 4; j++) { if (g[i][j] == 1) { dfs(g, i, j); cnt++; } } }
检查完图中有几个连通块后,就判断,如果有一个,则说明5个数都连在一起,则ans++,如下:
if (cnt == 1) return true; else return false;
2.3 完整代码:
#include <bits/stdc++.h> using namespace std; int a[12] = {0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1}; int ans = 0; int tx[4] = {0, 1, 0, -1}, ty[4] = {1, 0, -1, 0}; //int g[3][4]; void dfs(int g[3][4], int i, int j) { g[i][j] = 0; //从右、下、左、上四个方向分别检测周围是否是连通的,即是否==1 for (int k = 0; k < 4; k++) { int x = i + tx[k]; int y = j + ty[k]; if (x >= 0 && x <= 2 && y >= 0 && y <= 3 && g[x][y] == 1) dfs(g, x, y); } return; } bool f(int a[]) { //将a变成二维矩阵的形式 int g[3][4]; for (int i = 0; i < 3; i++) { for (int j = 0; j < 4; j++) { g[i][j] = a[i * 4 + j]; } } //对g上的每一点进行连通性检查 int cnt = 0;//连通块的数目 for (int i = 0; i < 3; i++) { for (int j = 0; j < 4; j++) { if (g[i][j] == 1) { dfs(g, i, j); cnt++; } } } if (cnt == 1) return true; else return false; } int main() { do { if (f(a)) ans++; } while (next_permutation(a, a + 12));//生成全排列并且去重 cout << ans << endl; return 0; }
dfs()检测连通性算法可以参考下面的迷宫问题。
2.4 其他题型
迷宫问题:
(1)题目描述

(2)解决思路
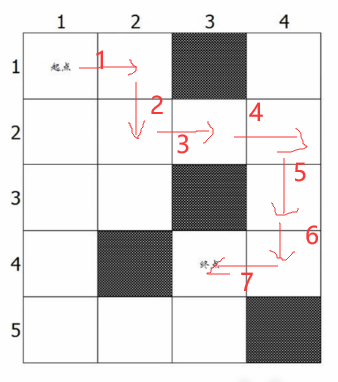
如上图,我们规定此图为一个二维数组a[5][4],0表示空地可以走,1表示有障碍物不可以走,并且规定往右、下、左、上分别进行探测。
定义代码如下:
int m, n, a[100][100], visit[100][100], start1, start2, p, q, step, Min = 10000;//start1,start2为起点位置下标;p,q为终点位置下标
从起点开始,先向右探测发现此处为a[1][2]==0可以走,step=1;然后在此位置向右探测,发现a[1][3]==1不可以走,则继续向下探测,发现此处a[2][2]==0可以走,step=2;依次循环探测直到到达终点,此时step==7;
接着回溯去找别的路线,此时的位置是终点,那么回溯上一个位置就是a[4][4]这个位置,在这个位置已经进行了右、下、左的位置探测了,并且都不可以走,则继续回溯上一个位置,直到能找到另一个可以走的位置为止,即a[2][2],往下就是另一条路线,继续执行右、下、左、上的探测操作,直到到达终点,又进行回溯,直到没有路线可走为止。
另外需要注意的是每走到一个位置就要标注此处为已访问,用visit[][] ==1表示;当回溯时需要把回溯过的位置都标注为未访问,用visit[][] == 0表示。
此为dfs()深度优先搜索算法的最短路径求解思路。
dfs的实现代码如下:
void dfs(int x, int y, int step) { if (x == p && y == q) { //结束条件:当下标x,y等于终点下标p,q时 if (step <= Min) Min = step; return; } //右 if (a[x][y + 1] == 0 && visit[x][y + 1] == 0) { visit[x][y + 1] = 1; //标为已访问 dfs(x, y + 1, step++); //右边的那个继续重复dfs操作 visit[x][y + 1] = 0; //当dfs结束后要回溯,把已访问过的标为未访问,变为初始状态,不然其他路咋走 } //下 if (a[x + 1][y] == 0 && visit[x + 1][y] == 0) { visit[x + 1][y] = 1; //标为已访问 dfs(x + 1, y, step++); //下边的那个继续重复dfs操作 visit[x + 1][y] = 0; //当dfs结束后要回溯,把已访问过的标为未访问,变为初始状态 } //左 if (a[x][y - 1] == 0 && visit[x][y - 1] == 0) { visit[x][y - 1] = 1; //标为已访问 dfs(x, y - 1, step++); //左边的那个继续重复dfs操作 visit[x][y - 1] = 0; //当dfs结束后要回溯,把已访问过的标为未访问,变为初始状态 } //上 if (a[x - 1][y] == 0 && visit[x - 1][y] == 0) { visit[x - 1][y] = 1; //标为已访问 dfs(x - 1, y, step++); //上边的那个继续重复dfs操作 visit[x - 1][y] = 0; //当dfs结束后要回溯,把已访问过的标为未访问,变为初始状态 } return ; }
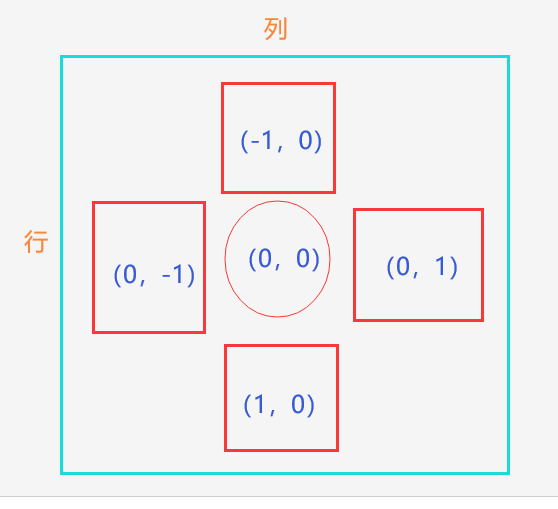
此处dfs的代码一共进行了四次循环,代码冗余,需要进行优化:将右、下、左、上的位置都用数组表示,行a[4]={0,1,0,-1}、列b[4]={1,0,-1,0},用x,y表示当前位置
优化后的代码:
for (int i = 0; i < 4; i++) { int t1, t2; t1 = x + x1[i]; t2 = y + y1[i]; if (a[t1][t2] == 0 && visit[t1][t2] == 0) { visit[t1][t2] = 1; dfs(t1, t2, step + 1); visit[t1][t2] = 0; } }
(3)实现代码
/* 迷宫问题 */ #include <iostream> using namespace std; int m, n, a[100][100], visit[100][100], p, q, step = 0, Min = 9999999; int x1[4] = {0, 1, 0, -1}, y1[4] = {1, 0, -1, 0}; void dfs(int x, int y, int step) { if (x == p && y == q) { //结束条件:当下标x,y等于终点下标p,q时 if (step < Min) Min = step; return; } for (int i = 0; i < 4; i++) { int t1, t2; t1 = x + x1[i]; t2 = y + y1[i]; if (a[t1][t2] == 0 && visit[t1][t2] == 0) { visit[t1][t2] = 1; dfs(t1, t2, step + 1); visit[t1][t2] = 0; } } return ; } int main() { int start1, start2; scanf("%d%d", &m, &n); for (int i = 1; i <= m; i++) { for (int j = 1; j <= n; j++) scanf("%d", &a[i][j]); } scanf("%d%d%d%d", &start1, &start2, &p, &q); visit[start1][start2] = 1; //把起点标志为已访问 dfs(start1, start2, 0); printf("%d", Min); return 0; } /* 测试样例: 5 4 1 1 2 1 1 1 1 1 1 1 2 1 1 2 1 1 1 1 1 2 1 1 4 3 */
(4)深度优先搜索(DFS )求解思路∶
1.先判断是否到达目标位置,如果到达目标位置,再试探有无其他更短的路径。
2.如果没有到达目标位置,则找到下一步可以到达的位置,直到找到目标位置。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号