作业三——K均值算法
1). 扑克牌手动演练k均值聚类过程:>30张牌,3类

可以看到,到第三轮结束,均值已不发生改变,故聚类中心已经稳定在[12, 8, 3],即Q、8、3
2). *自主编写K-means算法 ,以鸢尾花花瓣长度数据做聚类,并用散点图显示。(加分题)
鸢尾花花瓣长度分类——代码:
1 # 自主编写K-means算法 ,以鸢尾花花瓣长度数据做聚类,并用散点图显示 2 from sklearn.datasets import load_iris 3 import numpy as np 4 import random 5 6 iris = load_iris() 7 data = iris.data[:, 2] # 样本的花瓣长度 8 data.shape 9 n = len(data) # 样本个数(样本行数) 10 k = 3 # 类中心的个数 11 dist = np.zeros([n, k+1]) # 初始化距离矩阵,最后一列存放每个样本的类别/归属的类 12 # 1、选中心 13 center = random.sample(list(data), k) # 初始类中心,即随机选取三个样本的花瓣长度作为初始类中心 14 center_new = np.zeros(k) # 初始化新类中心 15 while True: 16 for i in range(n): 17 for j in range(k): 18 dist[i, j] = np.sqrt((data[i]-center[j])**2) # 2、求距离 19 dist[i, k] = np.argmin(dist[i, :k]) # 3、归类 (argmin返回最小值的下标) 20 21 # 4、求新类中心 22 for i in range(k): 23 index = dist[:, k] == i # 判断距离矩阵中最后一列归属为哪一列 24 center_new[i] = data[index].mean() # 属于该中心下的所有值的均值 25 # 5、判定结束 26 if (np.all(center == center_new)): # 判断新的类中心是否与上一轮的类中心相同 27 break 28 else: 29 center = center_new # 更新类中心 30 # 6、散点图展示 31 import matplotlib.pyplot as plt 32 plt.scatter(data, data, c=dist[:, k], cmap='rainbow') 33 plt.show()
鸢尾花花瓣长度分类——散点图:
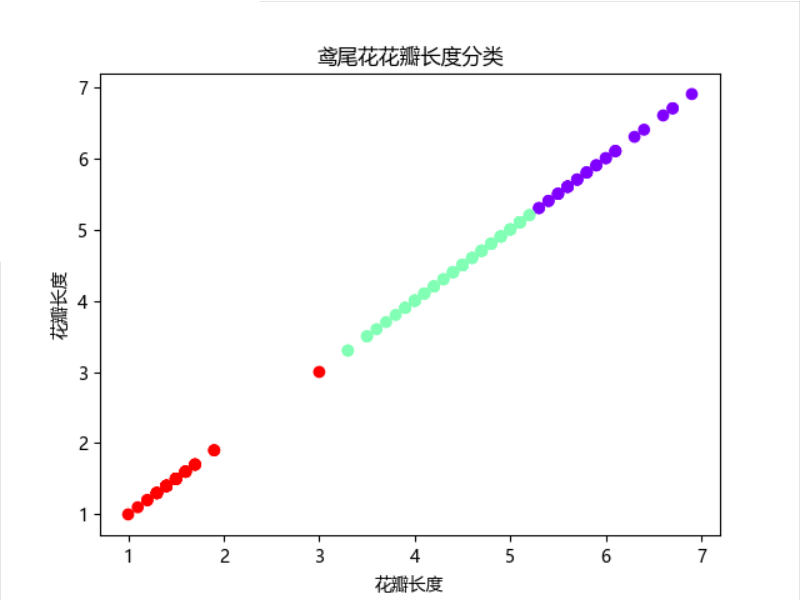
3). 用sklearn.cluster.KMeans,鸢尾花花瓣长度数据做聚类,并用散点图显示.
1 # 用sklearn.cluster.KMeans,鸢尾花花瓣长度数据做聚类,并用散点图显示. 2 # 1)导入数据集 3 from sklearn import datasets 4 data = datasets.load_iris() 5 X = data['data'][:, 2] # 获取花瓣长度 6 X = X.reshape(-1, 1) 7 # 2)构建模型 8 from sklearn import cluster 9 est = cluster.KMeans(n_clusters=3) 10 est.fit(X) 11 # 3)模型预测 12 y_means = est.predict(X) 13 # 4)绘图展示 14 import matplotlib.pyplot as plt 15 plt.scatter(X, X, c=y_means, cmap='rainbow') 16 plt.rcParams['font.sans-serif'] = ['Microsoft YaHei'] 17 plt.xlabel("花瓣长度") 18 plt.ylabel("花瓣长度") 19 plt.title("鸢尾花花瓣长度分类") 20 plt.show()
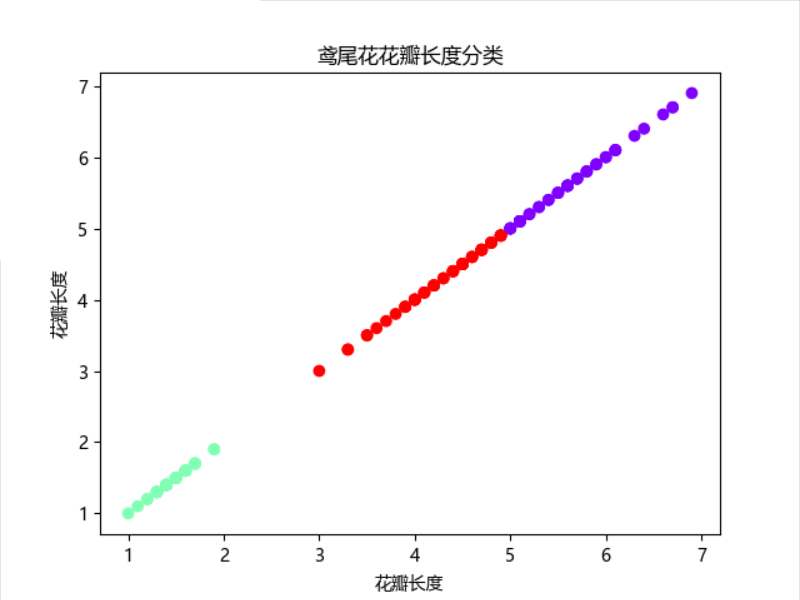
4). 鸢尾花完整数据做聚类并用散点图显示.
1 # 鸢尾花完整数据做聚类并用散点图显示 2 # 1)导入数据集 3 from sklearn import datasets 4 data = datasets.load_iris() 5 X = data['data'] # 获取完整数据 6 # 2)构建模型 7 from sklearn import cluster 8 est = cluster.KMeans(n_clusters=3) 9 est.fit(X) 10 est.cluster_centers_ 11 # 3)模型预测 12 y_means = est.predict(X)
四个属性类别分布画图
1 # 4)绘图展示 2 import matplotlib.pyplot as plt 3 plt.subplot(221) 4 plt.title("sepal length (cm)") 5 plt.rcParams['font.sans-serif'] = ['Microsoft YaHei'] 6 plt.scatter(X[:, 0], X[:, 0], c=y_means, cmap='rainbow') 7 plt.subplot(222) 8 plt.title("sepal width (cm)") 9 plt.scatter(X[:, 1], X[:, 1], c=y_means, cmap='rainbow') 10 plt.subplot(223) 11 plt.title("petal length (cm)") 12 plt.scatter(X[:, 2], X[:, 2], c=y_means, cmap='rainbow') 13 plt.subplot(224) 14 plt.title("petal length (cm)") 15 plt.scatter(X[:, 3], X[:, 3], c=y_means, cmap='rainbow') 16 plt.show()
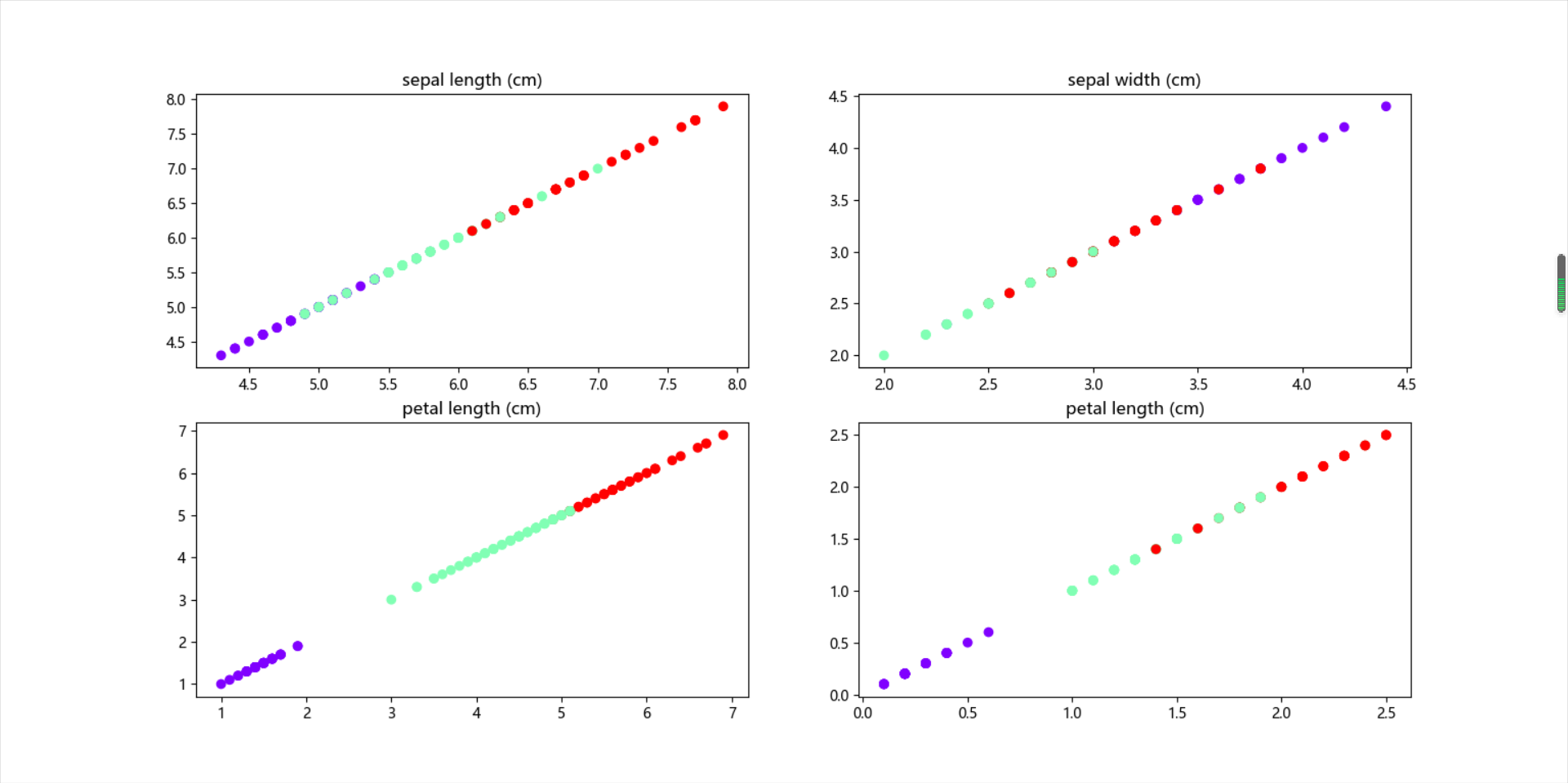
按花瓣和花萼分类画图
1 plt.rcParams['font.sans-serif'] = ['Microsoft YaHei'] 2 plt.subplot(121) 3 plt.scatter(X[:, 0], X[:, 1], c=y_means, cmap='rainbow') 4 plt.xlabel("花萼长度") 5 plt.ylabel("花萼宽度") 6 plt.title("花萼类别分布") 7 plt.subplot(122) 8 plt.scatter(X[:, 2], X[:, 3], c=y_means, cmap='rainbow') 9 plt.xlabel("花瓣长度") 10 plt.ylabel("花瓣宽度") 11 plt.title("花瓣类别分布") 12 plt.show()
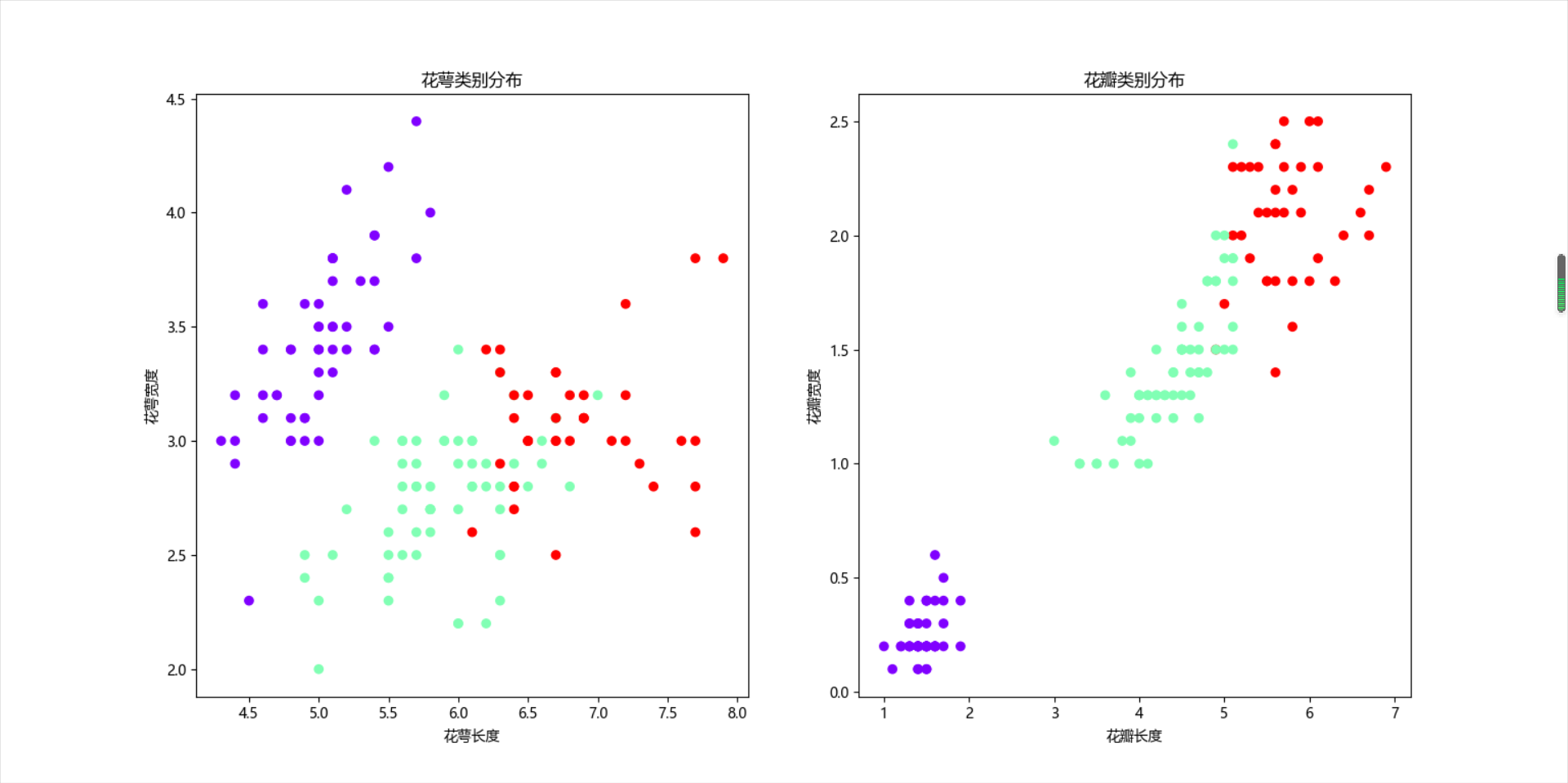
5).想想k均值算法可以用来做什么?
K-means算法通常可以应用于维数、数值都很小且连续的数据集,比如:从随机分布的事物集合中将相似度高的事物进行分组。
K-means算法典型的应用场景有:
1.文档分类器
根据标签、主题和文档内容将文档分为多个不同的类别。这是一个非常标准且经典的K-means算法分类问题。首先,需要对文档进行初始化处理,将每个文档都用矢量来表示,并使用术语频率来识别常用术语进行文档分类,这一步很有必要。然后对文档向量进行聚类,识别文档组中的相似性。
2.物品传输优化
使用K-means算法的组合找到无人机最佳发射位置和遗传算法来解决旅行商的行车路线问题,优化无人机物品传输过程。
3.识别犯罪地点
使用城市中特定地区的相关犯罪数据,分析犯罪类别、犯罪地点以及两者之间的关联,可以对城市或区域中容易犯罪的地区做高质量的勘察。
4.客户分类
聚类能过帮助营销人员改善他们的客户群(在其目标区域内工作),并根据客户的购买历史、兴趣或活动监控来对客户类别做进一步细分。对客户进行分类有助于公司针对特定客户群制定特定的广告。
5.球队状态分析
分析球员的状态一直都是体育界的一个关键要素。随着竞争越来愈激烈,机器学习在这个领域也扮演着至关重要的角色。如果你想创建一个优秀的队伍并且喜欢根据球员状态来识别类似的球员,那么K-means算法是一个很好的选择。
6.保险欺诈检测
机器学习在欺诈检测中也扮演着一个至关重要的角色,在汽车、医疗保险和保险欺诈检测领域中广泛应用。利用以往欺诈性索赔的历史数据,根据它和欺诈性模式聚类的相似性来识别新的索赔。由于保险欺诈可能会对公司造成数百万美元的损失,因此欺诈检测对公司来说至关重要。
7.乘车数据分析
面向大众公开的Uber乘车信息的数据集,为我们提供了大量关于交通、运输时间、高峰乘车地点等有价值的数据集。分析这些数据不仅对Uber大有好处,而且有助于我们对城市的交通模式进行深入的了解,来帮助我们做城市未来规划。
8.网络分析犯罪分子
网络分析是从个人和团体中收集数据来识别二者之间的重要关系的过程。网络分析源自于犯罪档案,该档案提供了调查部门的信息,以对犯罪现场的罪犯进行分类。
9.呼叫记录详细分析
通话详细记录(CDR)是电信公司在对用户的通话、短信和网络活动信息的收集。将通话详细记录与客户个人资料结合在一起,这能够帮助电信公司对客户需求做更多的预测。
10.IT警报的自动化聚类
大型企业IT基础架构技术组件(如网络,存储或数据库)会生成大量的警报消息。由于警报消息可以指向具体的操作,因此必须对警报信息进行手动筛选,确保后续过程的优先级。对数据进行聚类可以对警报类别和平均修复时间做深入了解,有助于对未来故障进行预测。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号