作业二——机器学习相关数学基础
P2 概率论与贝叶斯先验
一、概率论基础
1．概率与直观
（1）“九点分布”——本福特定律
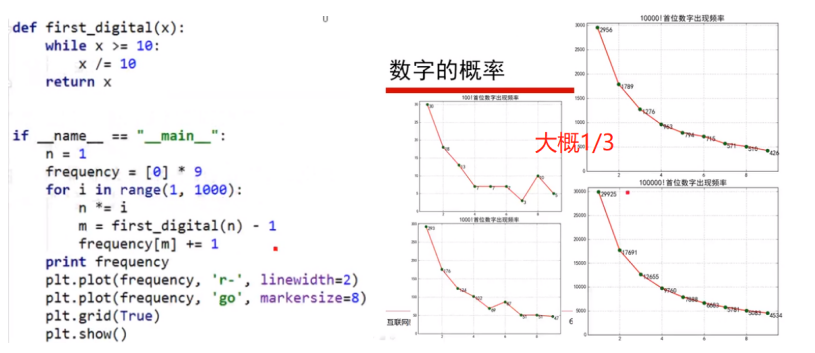
【归纳】
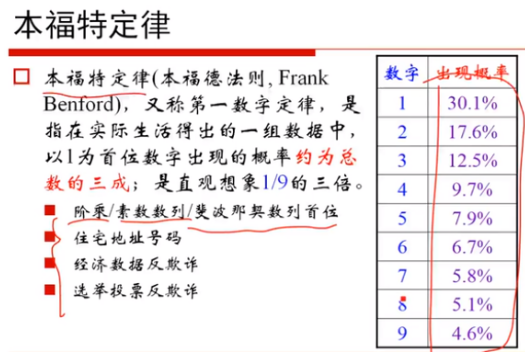
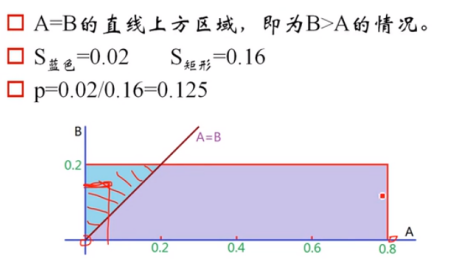
（2）推荐系统——相似用品A、随机用品B，求B>A的概率
（3）公路堵车概率模型——Nagel-Schreckenberg交通流模型
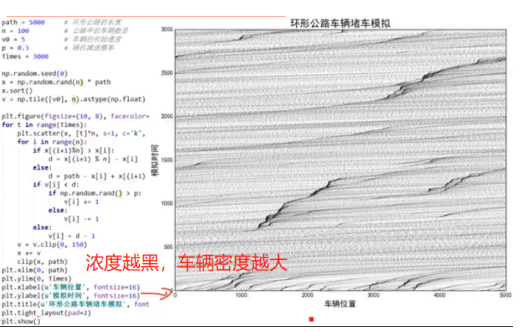
·减速概率的影响
2．常见概率分布
（1）概率公式
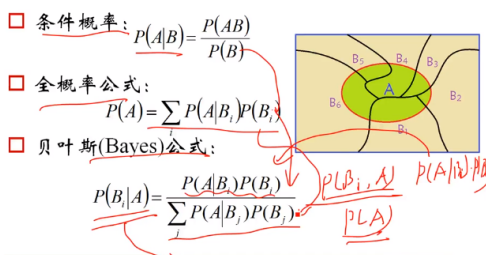
·贝叶斯公式拓展
额外点：“共轭”
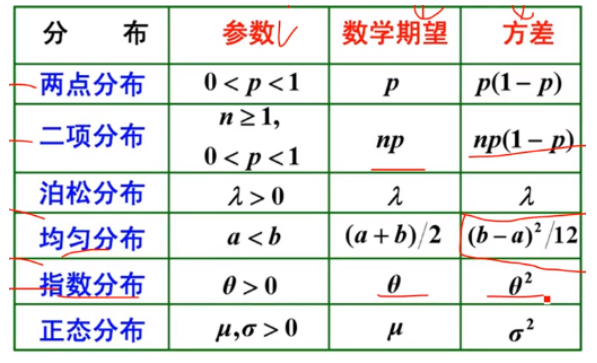
（2）常见分布
① 两点分布（0-1分布）
② 二项分布
③ Taylor展式
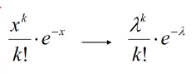
④ 泊松分布
⑤ 均匀分布
⑥ 指数分布——无记忆性
⑦ 正态分布
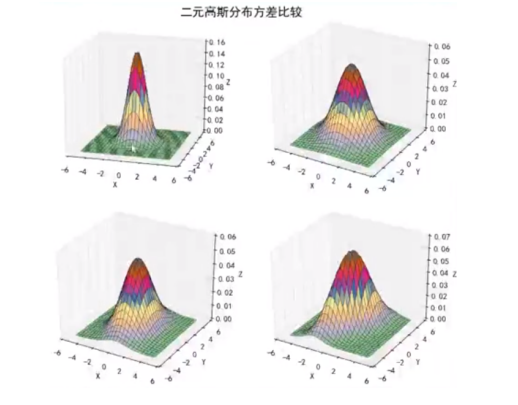
·扩展：二元正态分布（方差变大—矮胖；
np.diag(x,y),从上往下看，x=y圆，x≠y椭圆）
⑧ Beta分布
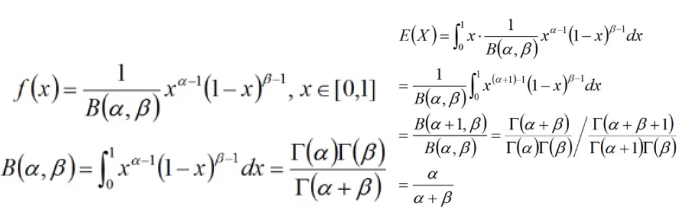
【归纳】
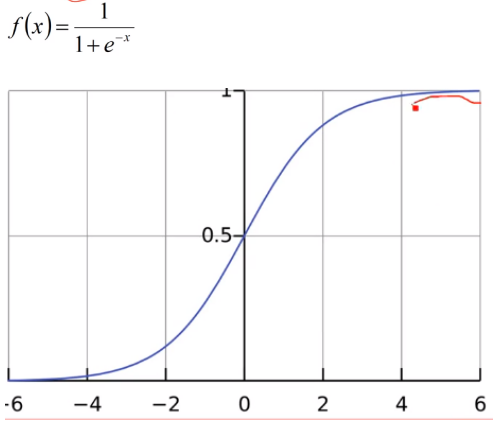
3．Sigmoid/Logistics函数的引入——广义的线性回归
二、统计量
1．期望/方差/协方差/相关系数
（1）期望
（2）方差
（3）协方差
·协方差的上界：
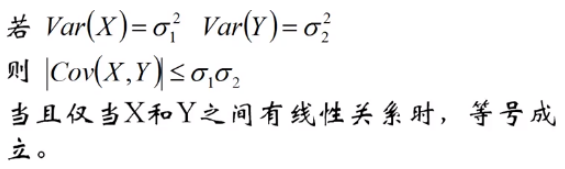
【注】协方差矩阵是对称阵
（4）Pearson相关系数
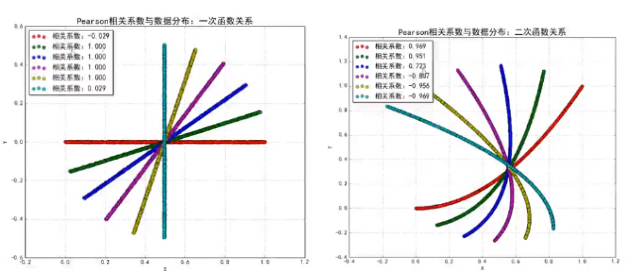
三、大数定律
四、中心极限定理
五、最大似然估计——过拟合
P3 矩阵和线性代数
一、矩阵
1．线性代数：SVD——特征值向量
应用：奇异值分解/PCA
2．矩阵的乘法/状态转移矩阵
（1）矩阵的乘法
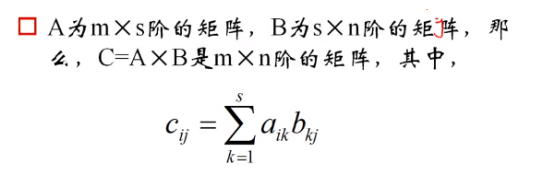
（2）状态转移矩阵
【补充】理解特征向量（如：物质动态平衡）
A每行相加等于1，与列矩阵1相乘等于1，即A的特征矩阵就为矩阵1
3．矩阵和向量的乘法
二、特征值和特征向量
【补充】迹
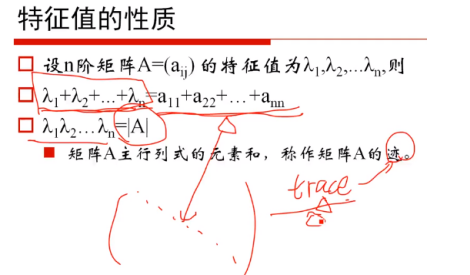
【总结】不同特征值对应的特征向量，线性无关。
1．对称阵、正交阵、正定阵
（1）正交阵：ATA=I
【注】A、B是正交矩阵，A×B也是正交矩阵。
（2）对称阵
实对称阵不同特征值的特征向量正交
（3）正定阵
任意m×n的矩阵A，ATA一定是半正定
2．数据白化/漂白——预处理
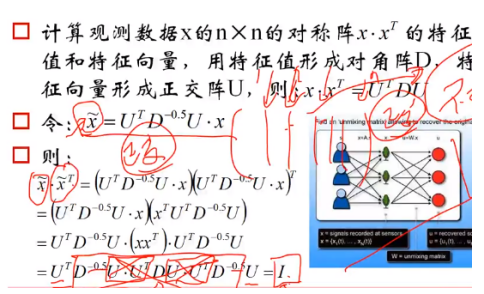
3．正交基——满秩求标准正交基
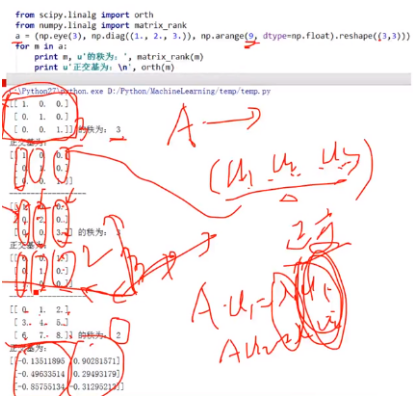
4．QR分解/LFM
（1）QR分解
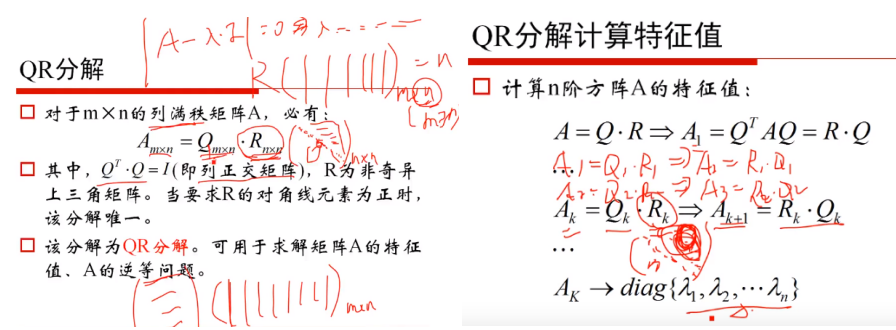
（2）LFM (Latent Factor Model)——用户对商品喜好的值
三、求导
1．矩阵对向量求导
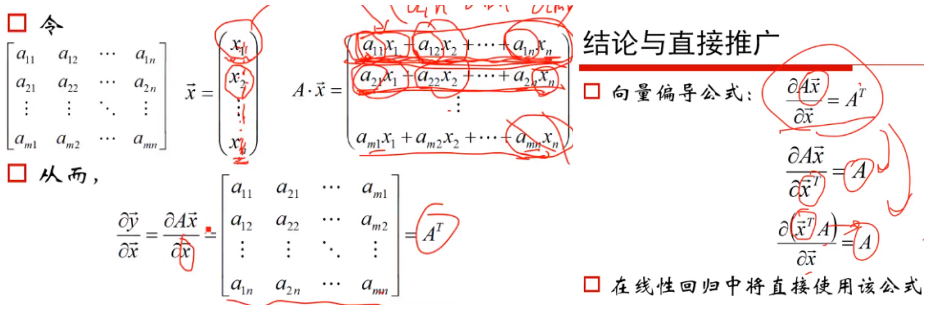
2．标量对向量求导
3．标量对方针求导
总结：用自己的话总结“梯度”，“梯度下降”和“贝叶斯定理”。
梯度可以认为是有特殊意义的有序数据集合，在构建模型最优化过程中，利用梯度的有序性能够不断循环迭代，获得最优解的值。
在梯度下降中，有序数据集合可分为三种情况：
1）单调递增
2）单调递减
3）先减后增
将数据集合以类似抛物线的形式呈现处理，以集合中的某个值为初始值，寻找比初始值更小的值点，最终找到最小值点（不是最小值），即为最优值。整个迭代过程成为梯度下降。
贝叶斯定理：假设在一般情况下，发生A的概率为p，但若发生B的前提下，发生A的概率大大提高/降低
