机器学习笔记之降维
一、降维概述
维数灾难(Curse of Dimensionality):通常是指在涉及到向量的计算的问题中,随着维数的增加,计算量呈指数倍增长的一种现象。在很多机器学习问题中,训练集中的每条数据经常伴随着上千、甚至上万个特征。要处理这所有的特征的话,不仅会让训练非常缓慢,还会极大增加搜寻良好解决方案的困难。这个问题就是我们常说的维数灾难。
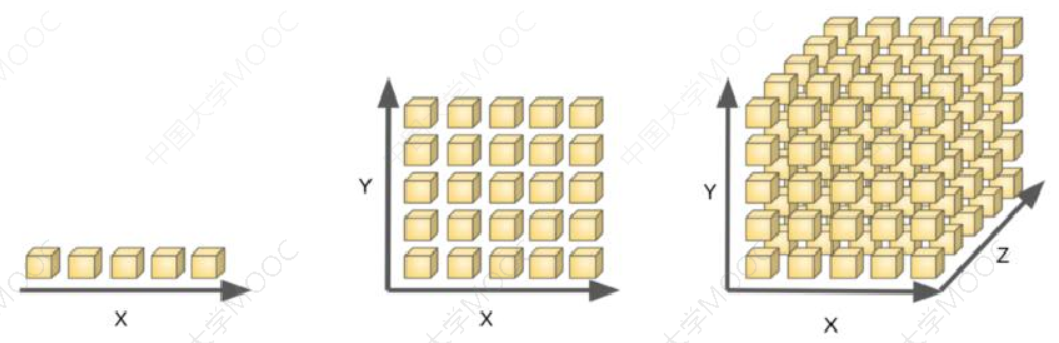
维数灾难涉及数字分析、抽样、组合、机器学习、数据挖掘和数据库等诸多领域。在机器学习的建模过程中,通常指的是随着特征数量的增多,计算量会变得很大,如特征达到上亿维的话,在进行计算的时候是算不出来的。有的时候维度太大也会导致机器学习性能的下降,并不是特征维度越大越好,模型的性能会随着特征的增加先上升后下降。
1.1 降维
什么是降维?
降维(Dimensionality Reduction)是将训练数据中的样本(实例)从高维空间转换到低维空间,该过程与信息论中有损压缩概念密切相关。同时要明白的,不存在完全无损的降维。有很多种算法可以完成对原始数据的降维,在这些方法中,降维
是通过对原始数据的线性变换实现的。
为什么要降维?
• 高维数据增加了运算的难度
• 高维使得学习算法的泛化能力变弱(例如,在最近邻分类器中,样本复杂度随着维度成指数增长),维度越高,算法的搜索难度和成本就越大。
• 降维能够增加数据的可读性,利于发掘数据的有意义的结构
1.2 降维的主要作用
1.减少冗余特征,降低数据维度
2.数据可视化
减少冗余特征:
假设我们有两个特征:
𝑥1:长度用厘米表示的身高;𝑥2:是用英寸表示的身高。
这两个分开的特征𝑥1和𝑥2,实际上表示的内容相同,这样其实可以减少数据到一维,只有一个特征表示身高就够了。很多特征具有线性关系,具有线性关系的特征很多都是冗余的特征,去掉冗余特征对机器学习的计算结果不会有影响。
数据可视化:
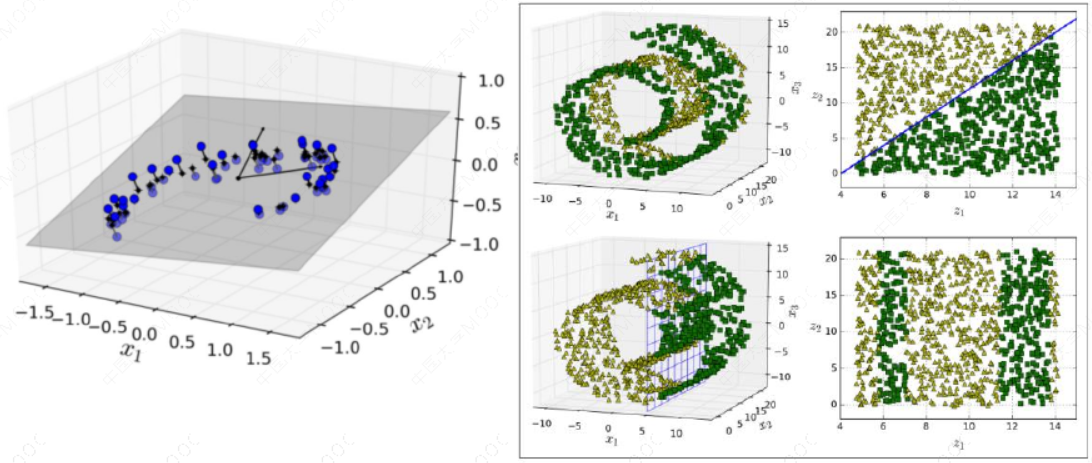
TSNE将数据点之间的相似度转换为概率。原始空间中的相似度由高斯联合概率表示,嵌入空间的相似度由“学生t分布”表示。虽然Isomap,LLE和variants等数据降维和可视化方法,更适合展开单个连续的低维的manifold。但如果要准确的可视化样本间的相似度关系,如对于下图所示的S曲线(不同颜色的图像表示不同类别的数据),t-SNE表现更好。因为t-SNE主要是关注数据的局部结构。
1.3 降维的优缺点
降维的优点:
• 通过减少特征的维数,数据集存储所需的空间也相应减少,减少了特征维数所需的计算训练时间;
• 数据集特征的降维有助于快速可视化数据;
• 通过处理多重共线性消除冗余特征。
降维的缺点:
• 由于降维可能会丢失一些数据;
• 在主成分分析(PCA)降维技术中,有时需要考虑多少主成分是难以确定的,往往使用经验法则
二、SVD(奇异值分解)
奇异值分解 (Singular Value Decomposition,以下简称 SVD)是在机器学习领域广泛应用的算法,它不光可以用于降维算法中的特征分解,还可以用于推荐系统,以及自然语言处理等领域。是很多机器学习算法的基石。
SVD可以将一个矩阵 𝐴分解为三个矩阵的乘积:
- 一个正交矩阵 𝑈(orthogonal matrix),
- 一个对角矩阵𝛴 (diagonal matrix),
- 一个正交矩阵𝑉的转置。
假设矩阵 𝐴 是一个 𝑚 × 𝑛 的矩阵,通过SVD是对矩阵进行分解,那么我们定义矩阵 𝐴 的 SVD 为:\(𝐴 = 𝑈𝛴𝑉^𝑇\)
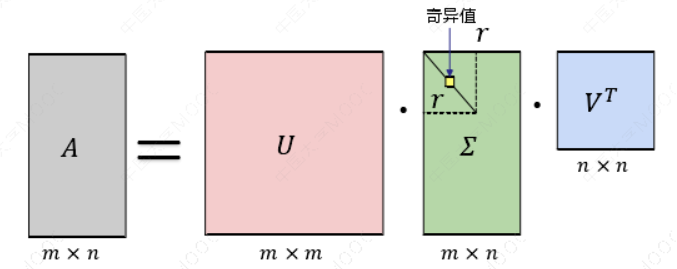
2.1 符号定义:
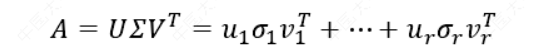
𝑈是一个𝑚 × 𝑚的矩阵,每个特征向量𝑢𝑖叫做𝐴 的左奇异向量。
𝛴是一个𝑚 × 𝑛的矩阵,除了主对角线上的元素以外全为 0,主对角线上的每个元素都称为奇异值 𝜎。
𝑉是一个𝑛 × 𝑛的矩阵,每个特征向量𝑣𝑖叫做 𝐴 的右奇异向量。
𝑈 和 𝑉都是酉矩阵,即满足:\(𝑈^𝑇𝑈 = 𝐼, 𝑉^𝑇𝑉 = 𝐼\)。𝑟为矩阵𝐴的秩(rank)。
2.2 SVD求解:
𝑈矩阵求解:
将\(𝐴𝐴^𝑇\)的所有特征向量组成一个 𝑚 × 𝑚的矩阵𝑈,就是我们 𝑆𝑉𝐷 公式里面的𝑈 矩阵了。一般我们将𝑈中的每个特征向量叫做𝐴 的左奇异向量。
注意:\(𝐴𝐴^𝑇 = (𝑈𝛴𝑉^𝑇)(𝑈𝛴𝑉^𝑇)^𝑇 = 𝑈(𝛴𝛴^𝑇)𝑈^𝑇\)
上式证明使用了\(𝑉^𝑇𝑉 = 𝐼, 𝛴^𝑇 = 𝛴\)。可以看出的\(𝐴𝐴^𝑇\)特征向量组成的矩阵就是我们 SVD 中的 𝑈矩阵.
𝑉矩阵求解:
如果我们将 𝐴 的转置和 𝐴 做矩阵乘法,那么会得到𝑛 × 𝑛 的一个方阵\(𝐴^𝑇𝐴\)。既然$ 𝐴^𝑇𝐴$是方阵,那么我们就可以进行特征分解,得到的特征值和特征向量满足下式:
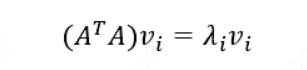
这样我们就可以得到矩阵 \(𝐴^𝑇𝐴\)的 𝑛个特征值和对应的𝑛个特征向量𝑣了。将 \(𝐴^𝑇𝐴\)的所有特征向量组成一个 𝑛 × 𝑛 的矩阵𝑉,就是我们 SVD 公式里面的 𝑉 矩阵了。一般我们将 𝑉中的每个特征向量叫做 𝐴 的右奇异向量。
注意:由于\(𝐴^𝑇𝐴 = (𝑈𝛴𝑉^𝑇)^𝑇(𝑈𝛴𝑉^𝑇) = 𝑉(𝛴^𝑇𝛴)𝑉^𝑇\)
上式证明使用了\(𝑈^𝑇𝑈 = 𝐼, 𝛴^𝑇 = 𝛴\)。可以看出\(𝐴^𝑇𝐴\)的特征向量组成的矩阵就是我们 SVD 中的 𝑉 矩阵。
𝛴 矩阵求解:
我们还可以看出我们的特征值矩阵等于奇异值矩阵的平方,也就是说特征值和奇异值满足如下关系:𝜎𝑖= 𝜆𝑖。这样也就是说,我们可以不用 𝜎𝑖=𝐴𝑣𝑖/𝑢𝑖来计算奇异值,也可以通过求出\(𝐴^𝑇𝐴\)的特征值取平方根来求奇异值。由于奇异值矩阵𝛴除了对角线上是奇异值,而其他位置都是 0,那我们只需要求出每个奇异值 𝜎就可以了。
我们注意到:\(𝐴 = 𝑈𝛴𝑉^𝑇,则:𝐴𝑉 = 𝑈𝛴𝑉^𝑇𝑉\)
由于:\(𝑉^𝑇𝑉 = 𝐼\),则:𝐴𝑉 = 𝑈𝛴得到:𝐴𝑣𝑖= 𝜎𝑖𝑢𝑖,𝜎𝑖= 𝐴𝑣𝑖/𝑢𝑖
这样我们可以求出我们的每个奇异值,进而求出奇异值矩阵 𝛴。
SVD计算案例:

两者都有相同的迹,都是50。

接着求出 \(𝐴𝐴^𝑇\)的特征值和特征向量:

最终得到 𝐴 的奇异值分解为:

SVD分解可以将一个矩阵进行分解,对角矩阵对角线上的特征值递减存放,而且奇异值减少特别的快,在很多情况下,前 10%甚至 1%的奇异值的和就占了全部的奇异值之和的 99%以上的比例。也就是说,对于奇异值,它跟我们特征分解中的特征值类似,我们也可以用最大的 𝑘 个的奇异值和对应的左右奇异向量来近似描述矩阵。
也就是说:
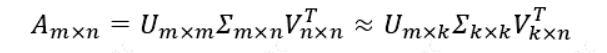
其中 𝑘 要比 𝑛小很多,也就是一个大的矩阵𝐴可以用三个小的矩阵\(𝑈_{𝑚×𝑘}, σ_{𝑘×𝑘}\), \(𝑉_{𝑘×𝑛}^𝑇\)来表示。
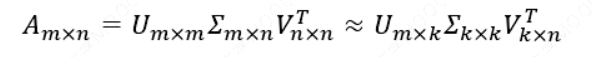
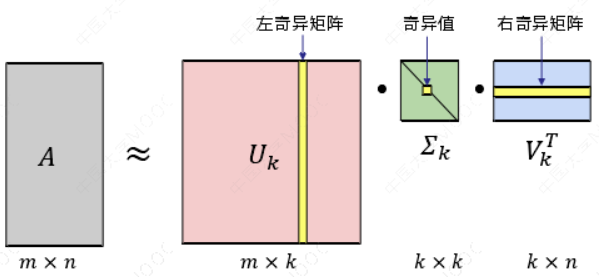
如图所示,现在我们的矩阵𝐴 只需要黄色的部分的三个小矩阵就可以近似描述了。
SVD案例:

三、PCA(主成分分析)
主成分分析(Principal Component Analysis,PCA)是一种降维方法,通过将一个大的特征集转换成一个较小的特征集,这个特征集仍然包含了原始数据中的大部分信息,从而降低了原始数据的维数。减少一个数据集的特征数量自然是以牺牲准确性为代价的,但降维的诀窍是用一点准确性换取简单性。因为更小的数据集更容易探索和可视化,并且对于机器学习算法来说,分析数据会更快、更容易,而不需要处理额外的特征。
主成分分析流程图:
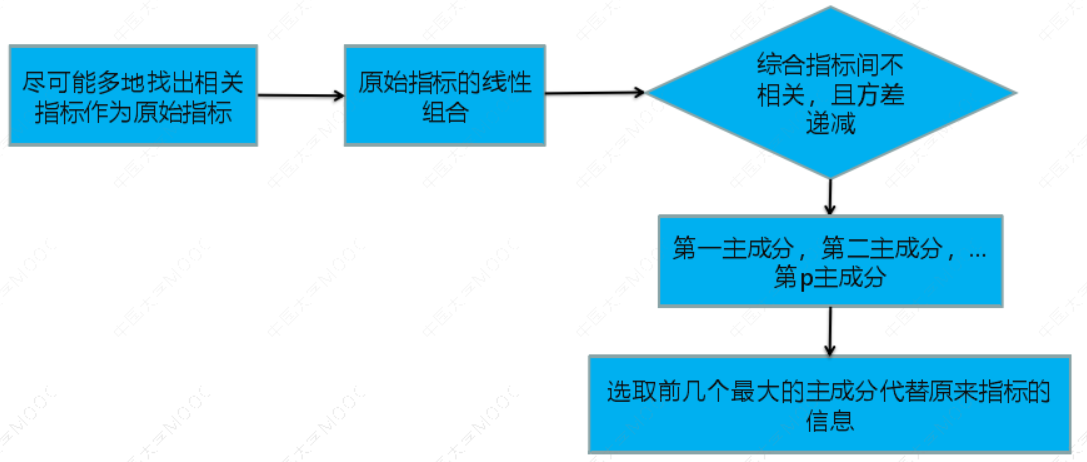
PCA的思想很简单——减少数据集的特征数量,同时尽可能地保留信息。
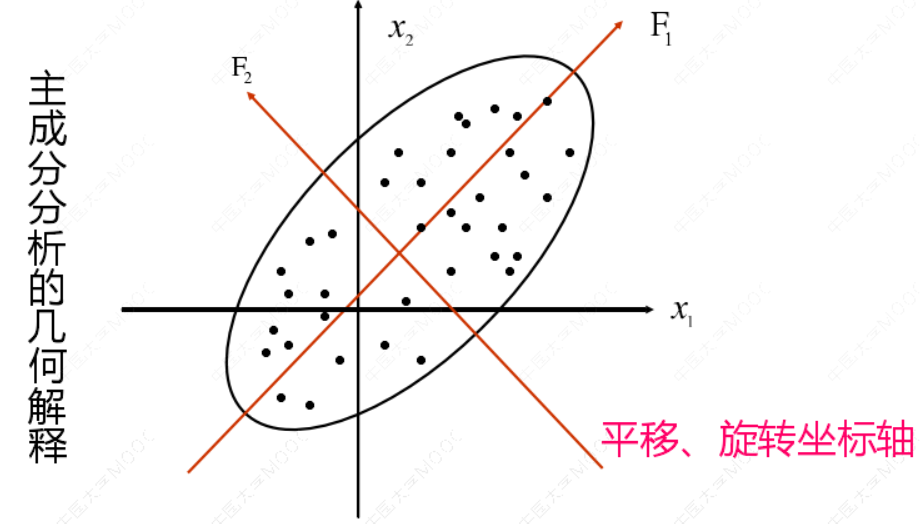
通过平移、旋转坐标轴,找到主成分pc1和pc2。
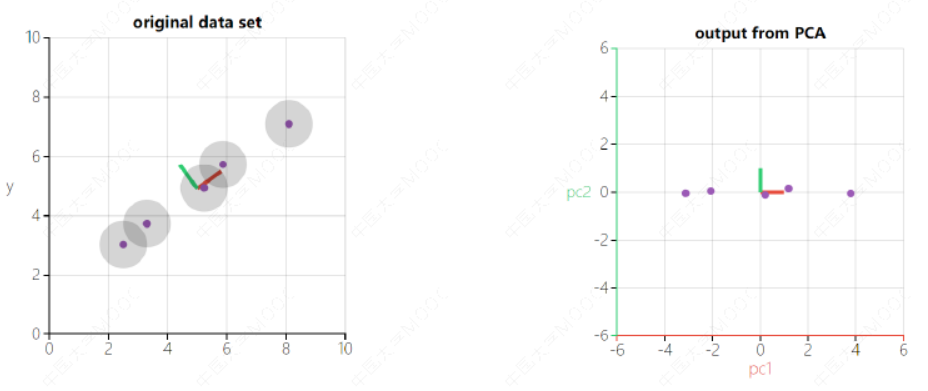
PCA识别在训练集中占最大方差量的轴。
在图1中,它是实线。 它还找到与第一个轴正交的第二个轴,它考虑了剩余方差的最大量。在这个2D示例中,没有选择:它是虚线。如果它是一个更高维的数据集,PCA还会找到与前两个轴正交的第三个轴,以及第四个,第五个等等 - 与数据集中的维数一样多的轴。
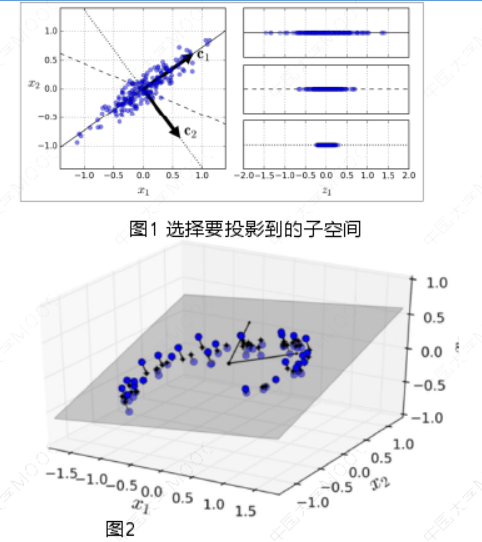
定义第 𝒊 轴的单位向量称为第 𝒊 个主成分 (PC) 。
• 在图1中,第一个 PC为 𝑐1,第二个 PC 为 𝑐2。
• 在图2中,前两个 PC由平面中的正交箭头表示,第三个 PC与平面正交(向上或向下)。
如何得到这些包含最大差异性的主成分方向呢?
通过计算数据矩阵的协方差矩阵,然后得到协方差矩阵的特征值特征向量选择特征值最大(即方差最大)的k个特征所对应的特征向量组成的矩阵。这样就可以将数据矩阵转换到新的空间当中,实现数据特征的降维。
3.1 PCA的算法两种实现方法:
(1) 基于SVD分解协方差矩阵实现PCA算法
PCA 减少𝑛维到𝑘维:
设有𝑚条𝑛维数据,将原始数据按列组成𝑛行𝑚列矩阵𝑋。
第一步是均值归一化。我们需要计算出所有特征的均值,然后令 𝑥𝑗= 𝑥𝑗− 𝜇𝑗(𝜇𝑗为均值)。如果特征是在不同的数量级上,我们还需要将其除以标准差 𝜎2。
第二步是计算协方差矩阵(covariance matrix)𝛴:
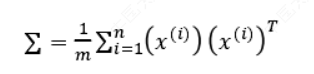
第三步是计算协方差矩阵𝛴的特征向量(eigenvectors),可以利用奇异值分解(SVD)来求解。
奇异值分解(SVD)的标准矩阵分解技术可以将训练集矩阵 𝐴 分解为三个矩阵 $𝑈 · 𝛴 · 𝑉^𝑇 \(的点积,其中\) 𝑉^𝑇$包含我们正在寻找的所有主成分。
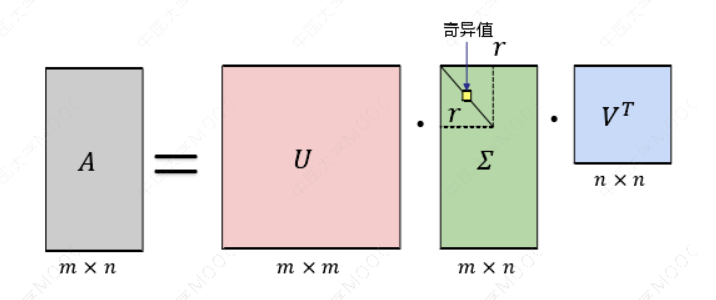
(2) 基于特征值分解协方差矩阵实现PCA算法
特征值与特征向量:如果一个向量𝑣是矩阵𝐴的特征向量,将一定可以表示成下面的形式:
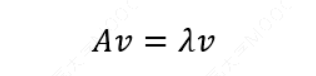
其中,𝜆是特征向量𝐴对应的特征值,一个矩阵的一组特征向量是一组正交向量。
特征值分解矩阵:对于矩阵𝐴 ,有一组特征向量𝑣 ,将这组向量进行正交化单位化,就能得到一组正交单位向量。特征值分解,就是将矩阵𝐴分解为如下式:
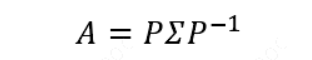
其中,𝑃是矩阵𝐴的特征向量组成的矩阵, 𝛴则是一个对角阵,对角线上的元素就是特征值。
设有𝑚条𝑛维数据,将原始数据按列组成𝑛行𝑚列矩阵𝑋.
第一步是均值归一化。我们需要计算出所有特征的均值,然后令 𝑥𝑗= 𝑥𝑗− 𝜇𝑗.(𝜇𝑗为均值)。如果特征是在不同的数量级上,我们还需要将其除以标准差 𝜎2。
第二步是计算协方差矩阵𝛴。
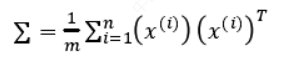
第三步是用特征值分解方法计算协方差矩阵𝛴的特征值和特征向量。
第四步是对特征值从大到小排序,选择其中最大的𝑘个。然后将其对应的𝑘个特征向量分别作为行向量组成特征向量矩阵𝑃。
第五步是将数据转换到𝑘个特征向量构建的新空间中,即 𝑌 = 𝑃𝑋。基变换。
3.2 PCA的算法案例:
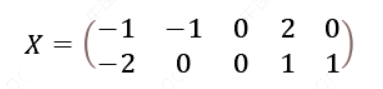
以这个为例,我们用PCA的方法将这组二维数据降到一维。 因为这个矩阵的每行已经是零均值,所以我们可以直接求协方差矩阵:

然后求σ的特征值和特征向量:
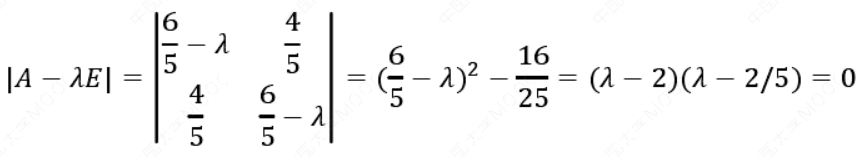
求解得到特征值:\(𝜆_1= 2,𝜆_2= 2/5\)
其对应的特征向量分别是:
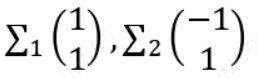
由于对应的特征向量分别是一个通解, σ1和σ2可取任意实数。那么标准化后的特征向量为:
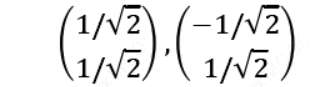
因此我们的矩阵𝑃是:
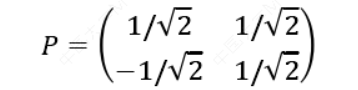
可以验证协方差矩阵σ的对角化:

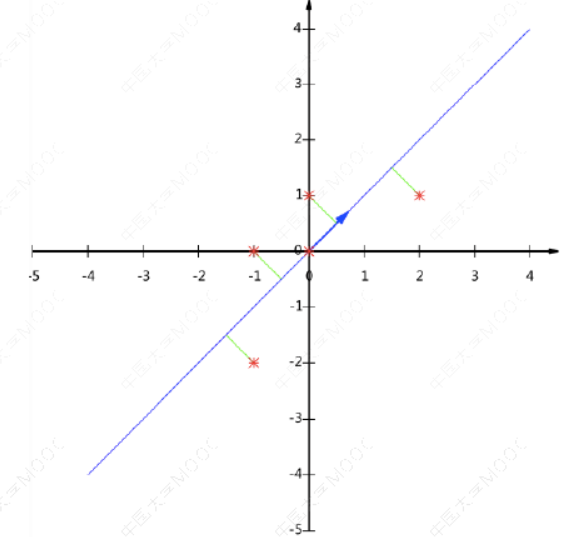
最后我们用𝑃的第一行乘以数据矩阵,就得到了降维后的数据表示:
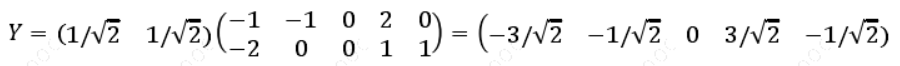
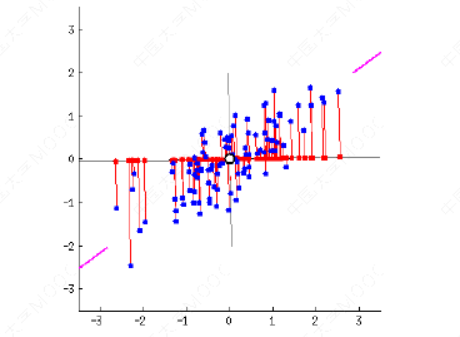
降维后的投影结果如下图:
3.3 PCA算法优缺点
PCA算法优点:
1.仅仅需要以方差衡量信息量,不受数据集以外的因素影响
2.各主成分之间正交,可消除原始数据成分间的相互影响的因素
3.计算方法简单,主要运算时特征值分解,易于实现
4.它是无监督学习,完全无参数限制的
PCA算法缺点:
1.主成分各个特征维度的含义具有一定的模糊性,不如原始样本特征的解释性强
2.方差小的非主成分也可能含有对样本差异的重要信息,因降维丢弃可能对后续数据处理有影响
四、参考资料
- Prof. Andrew Ng. Machine Learning. Stanford University
- 《统计学习方法》,清华大学出版社,李航著,2019年出版
- 《机器学习》,清华大学出版社,周志华著,2016年出版
- Christopher M. Bishop, Pattern Recognition and Machine Learning, Springer-Verlag, 2006
- Stephen Boyd, Lieven Vandenberghe, Convex Optimization, Cambridge University Press, 2004
- https://www.icourse163.org/course/WZU-1464096179

