hdu1506(dp)

Largest Rectangle in a Histogram

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 11219    Accepted Submission(s): 3074

Problem Description

A histogram is a polygon composed of a sequence of rectangles aligned at a common base line. The rectangles have equal widths but may have different heights. For example, the figure on the left shows the histogram that consists of rectangles with the heights 2, 1, 4, 5, 1, 3, 3, measured in units where 1 is the width of the rectangles:

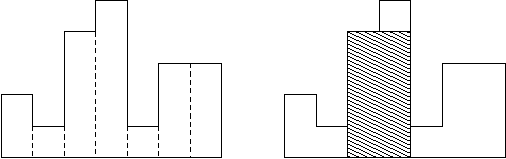
Usually, histograms are used to represent discrete distributions, e.g., the frequencies of characters in texts. Note that the order of the rectangles, i.e., their heights, is important. Calculate the area of the largest rectangle in a histogram that is aligned at the common base line, too. The figure on the right shows the largest aligned rectangle for the depicted histogram.

 

 

Input

The input contains several test cases. Each test case describes a histogram and starts with an integer n, denoting the number of rectangles it is composed of. You may assume that 1 <= n <= 100000. Then follow n integers h1, ..., hn, where 0 <= hi <= 1000000000. These numbers denote the heights of the rectangles of the histogram in left-to-right order. The width of each rectangle is 1. A zero follows the input for the last test case.

 

 

Output

For each test case output on a single line the area of the largest rectangle in the specified histogram. Remember that this rectangle must be aligned at the common base line.

 

 

Sample Input

7 2 1 4 5 1 3 3

4 1000 1000 1000 1000

0

 

 

Sample Output

8

4000

 

动态规划找出 a[i] 的左边和右边与自己连着的比自己大的数的长度 , 然后用这个长度乘以 a[i], 乘积最大的那个就是答案

用L[i]记录左边能到达的Id，r[i]记录右边能到达的Id，面积为(r[i]-L[i]+1)*a[i]

#include<stdio.h>
#include<string.h>
__int64 a[100010],L[100010],r[100010],max;
int main()
{
    int i,j,n,t;
    while(~scanf("%d",&n)&&n)
    {
        for(i=1; i<=n; i++)
            scanf("%I64d",&a[i]);
        L[1]=1;
        r[n]=n;
        for (i=2; i<=n; i++)
        {
            t=i;
            while (t>1 && a[i]<=a[t-1])
                t=L[t-1];
            L[i]=t;
        }
        for (i=n-1; i>=1; i--)
        {
            t=i;
            while (t<n && a[i]<=a[t+1])
                t=r[t+1];
            r[i]=t;
        }
        max=0;
        for(i=1; i<=n; i++)
        {
            if((r[i]-L[i]+1)*a[i]>max)
                max=(r[i]-L[i]+1)*a[i];
        }
        printf("%I64d\n",max);
    }
    return 0;
}