20145215《信息安全系统设计基础》第三周学习总结
20145215《信息安全系统设计基础》第三周学习总结
教材学习内容总结
信息的表示和处理
三种数字表示
- 无符号数:基于传统的二进制表示法,表示大于或等于零的数字
- 补码:表示有符号数,可为正可为负的数字
- 浮点数:表示实数的科学计数法的以二为基数的版本
- 整数运算和浮点数运算有不同的数学属性,因为它们处理数字表示有限性的方式不同,整数的表示虽然只能编码一个相对较小的数值范围,但这种表示精确;浮点数编码数值范围相对较大,但是近似的。
- 大量计算机的安全漏洞都是由计算机算术运算的微秒细节引发的
信息存储
-
字:
- 每个计算机都有一个字长,指明整数和指针数据的标称大小。因为虚拟地址是以这样的一个字来编码的,所以字长最重要的系统参数就是虚拟地址空间的最大大小。
- 对于一个字长为w位的机器而言,虚拟地址的范围为
0~2^w-1,程序最多访问2^w字节。
-
使用C99特性:当没有-m32或-m64参数时,一般情况下会生成跟操作系统位数一致的代码;
gcc -m32可以在64位机上(比如实验楼的环境)生成32位的代码 -
字节顺序:字节顺序是网络编程的基础,是指占内存多于一个字节类型的数据在内存中的存放顺序,通常有小端、大端两种字节顺序。
- 小端法:低字节数据存放在内存低地址处,高字节数据存放在内存高地址处。
- 大端法:高字节数据存放在低地址处,低字节数据存放在高地址处。

布尔代数
-
逻辑运算:
- 所有逻辑运算都可以用与、或、非表达(最大式、最小式)而与或非可以用“与非”或“或非”表达,所以,只要一个与非门,就可以完成所有的逻辑运算
- 逻辑运算符:
逻辑与(&&);逻辑或(||);逻辑非(!)
-
位运算:结果是位向量;
按位与(&) 二进制每一位遇0为0;按位或(|) 二进制每一位遇1为1;按位异或(^) 0^0=0,0^1=1,1^0=1,1^1=0;按位取反(~) 二进制每一位取反 -
掩码运算:掩码是位运算的重要应用,这里掩码是一个特定位模式,表示从一个字中选择一个位的集合。对特定位可以置一,可以清零。
整数表示
-
无符号数编码:对于长度为w的位向量,都有一个唯一的值与之对应;反过来,在0~2^w-1之间的每一个整数都有一个唯一的长度为w的位向量二进制表示与之对应。
-
补码编码:
- 补码形式是最常见的有符号数的计算机表示方式
- 将字的最高有效位解释为负权 B2T(W)函数为:B2T(x) = -x(w-1)2(w-1)+∑xi2i(求和从i=0到i=w-2)
-
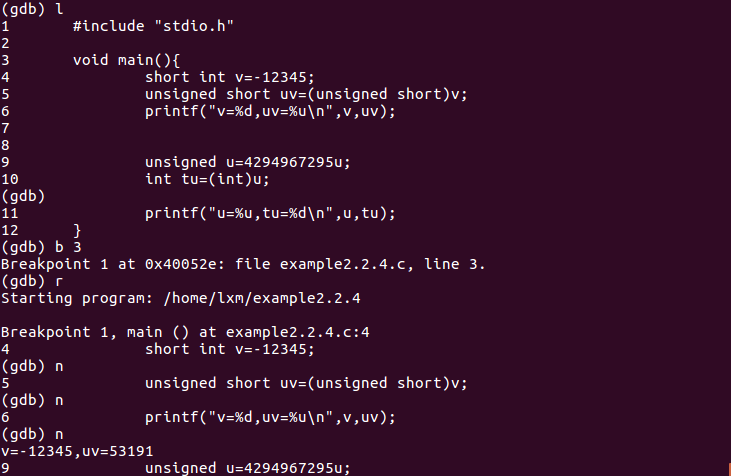
有符号数和无符号数之间的转换:
- 处理同样字长的有符号数和无符号数之间相互转换的一般规则:数值可能会改变,但是位模式不变。
- c语言允许无符号数和有符号数之间的转换,转换的原则是底层的位表示不变。
- 当从无符号数转换为有符号数是,效果是应用函数U2T,从有符号数转化为无符号数时,应用函数T2U,其中w表示数据类型的位数。

-
扩展一个数字的位表示:
- 零扩展:要将一个无符号数转换为一个更大的数据类型,只需简单的最高位前加0。
- 符号扩展:将一个补码数字转换为一个更大的数据类型,在表示中添加最高有效位值的副本。

-
截断数字:不用额外的位来扩展一个数值,而是减少表示一个数字的位数。
-
使用无符号数的情况:
- 把字仅仅看做是位的集合,并没有任何数字意义时。
- 当实现模运算和多精度运算的数学包时,数字是由数的数组来表示的,无符号值也会非常有用。
整数运算
-
无符号加法:
- 无符号运算可以被视为一种模运算形式,无符号加法等同于计算和摸上2^w,可以通过简单的丢弃x+y的w+1位表示的最高位,来计算这个数值。
- 一个算数运算的溢出,是指完整的整数结果不能放到数据类型的字长限制中去。判断无符号运算是否溢出,例如
s=x+y(s、x、y均为无符号数),则唯一可靠的判断标准就是s<x或s<y。
-
补码加法:两个数的w位补码之和与无符号之和有完全相同的位级表示。大多数计算机用相同的机器指令来执行无符号或者有符号加法。 有符号加法的结果z=x+y可分为4种情况:
- -2(w)≤z<-2(w-1):两个负数相加得一个非负的结果
- -2^(w-1)≤z<0:结果正常,z为负数
- 0≤z<2^(w-1):结果正常,z为正数
- 2(w-1)≤z<2(w):两个正数相加得一个负数的结果
-
补码的非:
- 对于范围-2(w-1)≤x<2(w-1)内的x,补码的非运算如下:x=-2(w-1):补码的非为-2(w-1);x>-2^(w-1):补码的非为-x。
- 位级补码非:对每一位求补,再对结果+1。
-
无符号乘法:两个数x、y相乘且x、y的位数为w,则结果的位数为2w。
-
补码乘法:同无符号乘法。若为截断后的结果,则取结果的后w位作为计算结果。无符号运算和补码运算在“+”、“-”、“*”在位级上有相同的结果。
-
乘以常数:对于某个常数K的表达式x*K生成代码,编译器会将K的二进制表示表达为一组0或1的交替的序列: [(0…0)(1…1)(0…0)…(1…1)],可以用以下两种形式来计算这些乘积的结果:
- A:(x<<n)+(x<<n-1)+……+(x<<m)
- B:(x<<n+1)-(x<<m)
-
除以2的幂:设x/K,令K=2^n,
- 当x为正数时,计算 x>>n;
- 当x为负数时,将x加上偏置量,即加上2^n-1(即K-1),计算** (x+偏置量)>>n**。
浮点数
-
浮点表示对形如 V=x*2^y 的有理数进行编码;适用于:非常大的数字(|V|>>0)、非常接近于0的数字(|V|<<1)、实数运算的近似值;IEEE浮点标准:IEEE标准754。
-
二进制小数:
- 二进制点左边第i位,权为2i;右边第i位,权为(1/2)i。
- 增加二进制表示的长度可以提高表示的精度。
-
IEEE浮点格式:
- 表示形式:
V=(-1)^s * M * 2^E - 符号:s决定这个数是正还是负。0的符号位特殊情况处理。
- 尾数:M是一个二进制小数,范围为12-ε或者01-ε,ε=(1/2)^n。
- 阶码:E对浮点数加权,权重是2的E次幂(可能为负数)。
- 表示形式:
-
根据阶码的值,被编码的值可分为三种:
- 情况一:规格化的值(当阶码字段不全为0或全为1时),
阶码 E = e-Bias(e为无符号整数);偏置值 Bias = 2^(k-1)-1;尾数 M = 1+f(小数字段frac的解释为描述小数值f,二进制小数点在小数字段最高有效位的左边)。 - 情况二:非规格化的值 (当阶码字段全为0时),
E = 1-Bias;Bias = 2^(k-1)-1;M = f。 - 情况三:特殊值 (当阶码字段全为1时),当小数域全为0时, 当s=1时,为-∞;当s=0时,为+∞;当小数域不全为0时,为NaN。
- 情况一:规格化的值(当阶码字段不全为0或全为1时),
-
浮点数的舍入:IEEE浮点格式定义了四种不同的舍入方法:
- 向偶舍入(默认):将数字向上或向下舍入,是的结果的最低有效数字为偶数。能用于二进制小数。
- 向零舍入:把整数向下舍入,负数向上舍入。
- 向下舍入:正数和负数都向下舍入。
- 向上舍入:正数和负数都向上舍入。
-
浮点运算:
- 浮点加法:不满足结合性、满足单调性
- 浮点乘法:不满足结合性、满足单调性,在加法上不满足分配性
遇到的问题和解决过程
-
运行Perl脚本出现问题:

一开始在网上找了很多解决方法都没有用,后来简单学习了一下Perl脚本发现是自己理解错误,所以命令也就自然用错了。首先,Perl程序的第一行是以#开头的,它指定了perl程序的解释器,如果不知道Perl指令的存放位置,可以使用which指令查看。

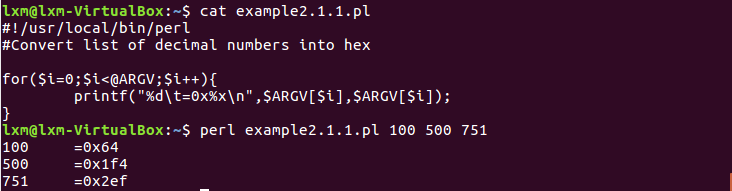
修改完第一行的存放位置之后,有两种方法可以运行Perl文件:- 第一种:通过
perl调用*.pl,把脚本的文件名当作perl程序的参数:perl *.pl,由于教材上的这个文件需要我们传入参数,所以执行perl example2.1.1.pl 100 500 751(我命名的文件名是:example2.1.1.pl)即可,perl还可以接受其它的选项。
- 第二种:直接调用
*.pl,首先需要给*.pl添加可以执行(x)权限:chmod a+x *.pl,然后像调用普通的执行文件一行执行*.pl即可:./*.pl。

- 第一种:通过
-
运行教材35页
reverse_array代码时,发现代码对偶数长度的数组能正常工作,但是当数组长度为奇数时,中间元素会被设置为0:
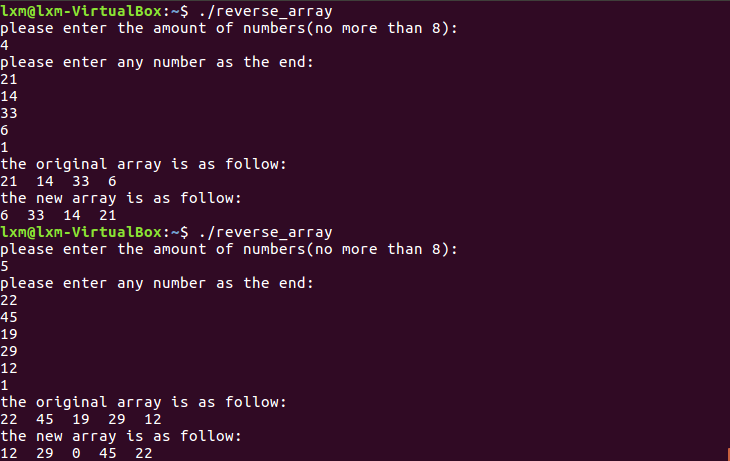
调试的时候会发现由于在最后一次调用inplace_swap的时候,赋值给first和last变量的都是原数组中最中间的数字,所以在第一处*y = x^y时,y指向的数字就变为了0,此后,0作为最中间数字进入循环。因此直接把reverse_array代码中循环条件改为first<last即可,因为正中间的元素不需要进行交换。

本周代码托管


代码托管地址:click here
心得体会
这周最大的收获就是对信息=位+上下文这个概念有了进一步理解,前两周一直不太清楚这个公式到底意味着什么,直到这周学习完第二章之后才有些新的感触。例如,我们的hello程序的生命是从一个源程序开始的,这个源程序由程序员通过编辑器创建并保存为文本文件,文件名就是hello.c。源程序实际上就是一个由0和1组成的位(又称为比特)序列,这些位被组织8个一组,称为字节,每个字节都表示程序中某个文本字符。hello.c的表示方法也说明了一个基本的思想:系统中所有的信息都是由一串比特表示的。区分不同数据对象的唯一方法是我们读到这些数据对象时的上下文。比如,在不同的上下文中,同样的字节序列可能表示一个整数、浮点数、字符串或者及其指令。这个概念也会为我们理解计算机内部一些信息的处理方式会起到很大的帮助。
学习进度条
| 代码行数(新增/累积) | 博客量(新增/累积) | 学习时间(新增/累积) | 重要成长 | |
|---|---|---|---|---|
| 目标 | 5000行 | 30篇 | 400小时 | |
| 第一周 | 0/0 | 1/2 | 25/45 | 学习了几个Linux核心命令 |
| 第二周 | 55/55 | 2/4 | 27/72 | 学会了vim,gcc以及gdb的基本操作 |
| 第三周 | 148/203 | 1/5 | 23/95 | 对信息的表示和处理有更深入的理解 |



