1.本周学习总结
1.1思维导图

1.2.对树的认识及学习体会
感觉从树开始,数据结构这门课的难度一下子升高了不少。对于树的题目,感觉有点不知如何下手,一个问题的解决思路都没有办法结合树的内容想出来。平时的pta编程题打起来着实困难,即使知道此问题的做法,却还是不能用代码来实现。
2.PTA实验作业
2.1.题目1:6-4 jmu-ds-表达式树
2.1.1设计思路
建表达式二叉树
建op栈,op.push('#')
初始化根节点栈:stacktree栈
while(表达式未结束)
if(ch==操作数)
then 生成一个只有根结点的子树T stacktree.push(T)
if(ch==运算符)
then
while(ch<op栈顶运算符) 栈顶优先级高,则
创建一个树结点T,数据为op.top()
stacktree弹出2个根结点T1,T2
T->lchild=T1,T->rchild=T2
stacktree.push(T)
if(ch>op顶运算符) op.push(ch)
if(ch==op顶运算符) 则op.pop()
计算表达式树
double sum=0
if(T不为空)
then
if(左右子树不为空)
then 返回对应数值
递归左右子树得到a,b
switch(结点值)
case +:计算并返回a+b
case - : 计算并返回a-b
case * : 计算并返回a*b
case / :
if(除数为0)
then 直接输出错误并退出
else 计算并返回a/b
2.1.2代码截图

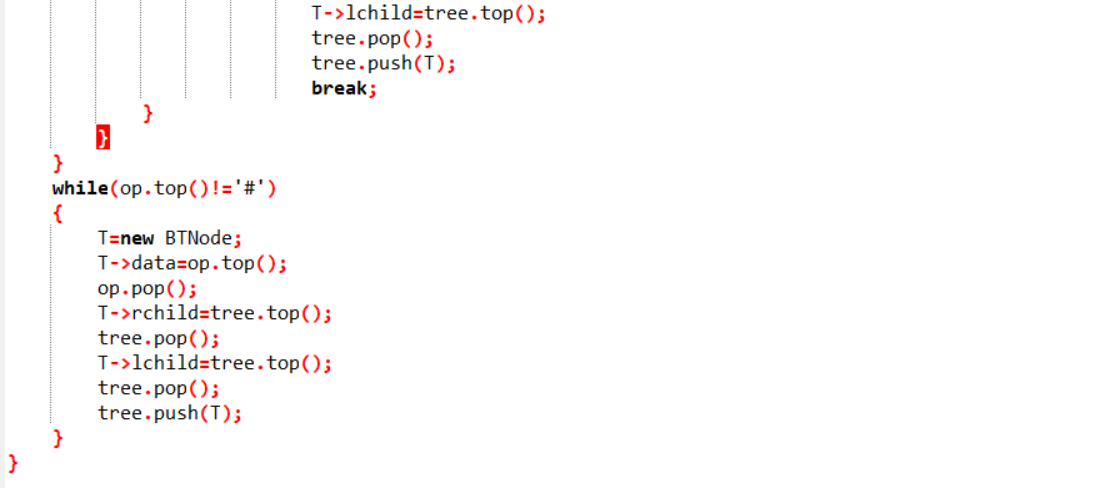

2.1.3本题PTA提交列表说明。

- Q1:编译错误
- A1:将rchild写成rchlid
2.2.题目2:7-4 jmu-ds-二叉树叶子结点带权路径长度和
2.2.1设计思路
BTree CreateBTree(int i)
设定BTree变量BT
if(i>str.size()-1) return NULL;
if(是'#',是空节点) return NULL;
为BT开辟一个空间
BT->data=str[i];
BT的lc应该是第2*i的元素
rc应该是第2*i+1的元素
return BT;
void GetWpl(BTree BT,int &wpl,int h)
定义h表示深度
先判断是否是叶子节点
if(BT->Left==NULL&&BT->Right==NULL)
wpl=深度*当前data的值
深度归零
h++
若是空节点,return
非空非叶
递归访问其左右子树
GetWPL(BT->Left,wpl,h);
GetWPL(BT->Right,wpl,h);
2.2.2代码截图
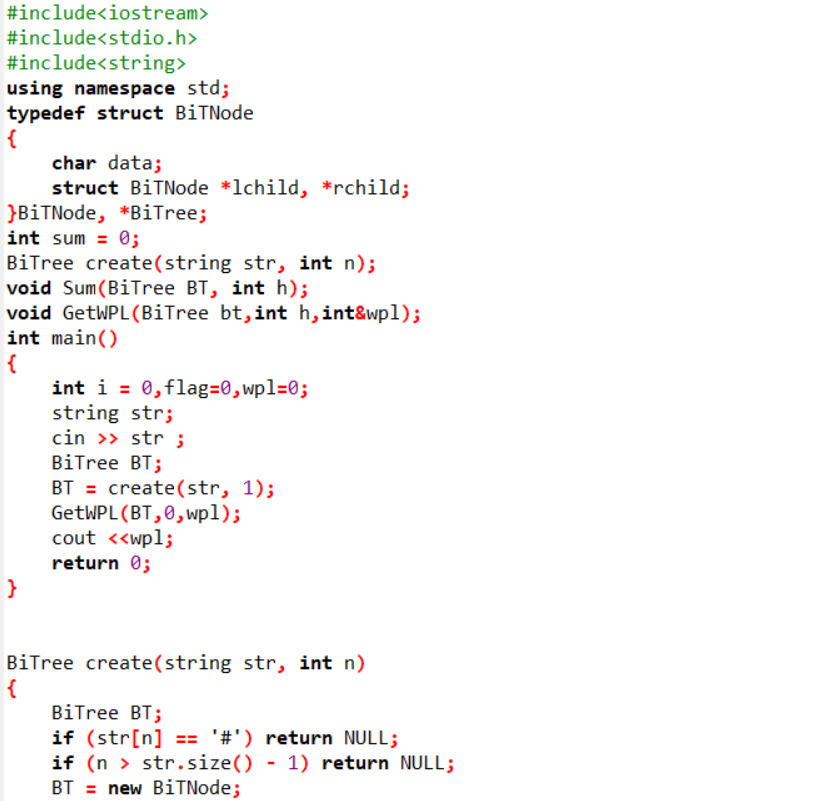

2.2.3本题PTA提交列表说明。

2.3.题目3:7-1 还原二叉树
2.3.1设计思路
int DFS(char a[],char b[],int n)
if结点个数非法
返回 0;
for i=0 to n
if数组a和数组b中的字符相等
break;
左子树高度x=DFS(a+1,b,i)+1;
右子树高度y=DFS(a+i+1,b+i+1,n-i-1)+1;
if x大于y
返回 x;
else
返回 y;
2.3.2代码截图
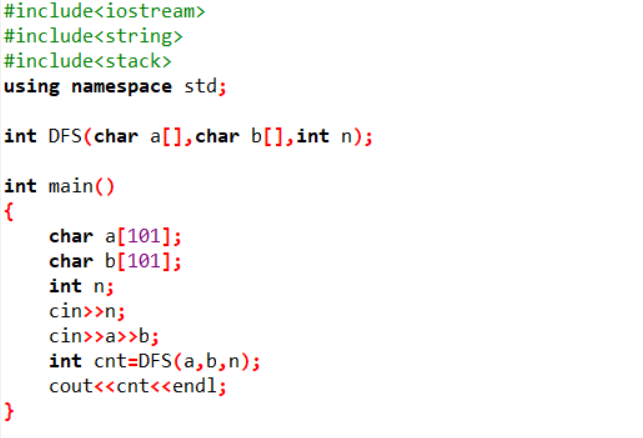

2.3.3本题PTA提交列表说明。

3、阅读代码
3.1 题目:计算一棵树的宽度(并输出每一层的宽度)
3.2 解题思路
这里需要用到二叉树的层次遍历,即广度优先周游。在层次遍历的过程中,通过读取队列中保留的上一层的节点数来记录每层的节点数,以获取所有层中最大的节点数。
3.3 代码截图


3.4 学习体会
通过此题,加成了对于层次遍历的做法,相对于前中后序遍历来说,层次遍历需要用队列辅助实现,对于代码的操作多了许多



