0010.无监督学习之K-均值聚类

一、聚类分析概述

聚类分析是无监督机器学习算法中最常用的一类，其目的是将数据划分成有意义或有用的组（也被称为簇）。组内的对象相互之间是相似的（相关的），而不同组中的对象是不同的（不相关的）。组内的相似性（同质性）越大，组间差别越大，聚类就越好。

1. 簇的定义

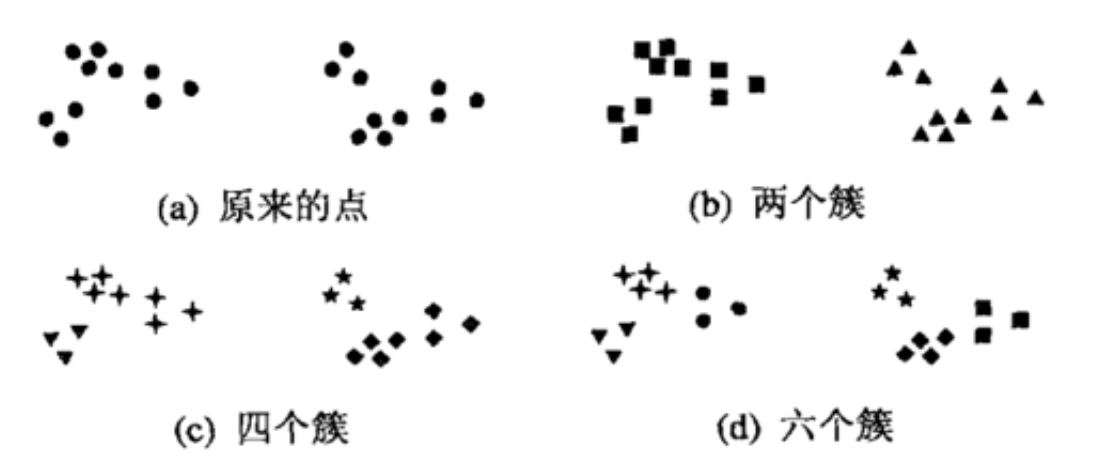
简单来说，簇就是分类结果中的类，但实际上簇并没有明确的定义，并且簇的划分没有客观标准，我们可以利用下图理解什么是簇。该图显示了20个点和将它们划分成簇的3种不同方法。标记的形状指示簇的隶属关系。下图分别将数据划分成两部分、四部分和六部分。将2个较大的簇每一个都划分成3个子簇可能是人的视觉系统造成的假象。此外，说这些点形成4个簇可能也不无道理。该图表明簇的定义是不精确的，而最好的定义依赖于数据的特性和期望的结果。

2. 常用的聚类算法

最常用的聚类算法有以下三种：

① Kmeans聚类：也成为K均值聚类，它试图发现k（用户指定个数）个不同的簇，并且每个簇的中心采用簇中所含值的均值计算而成；

② 层次聚类：层次聚类（hierarchical clustering）视图在不同层次对数据集进行划分，从而形成树形的聚类结构；

③ DBSCAN：这是一种基于密度的聚类算法，簇的个数由算法自动地确定。低密度区域中的点被视为噪声而忽略，因此DNSCAN不产生完全聚类。

二、K-均值聚类算法

K均值是发现给定数据集的k个簇的算法。簇个数k是用户给定的，每一个簇通过其质心（centroid）来描述。

K均值工作流程是这样的：首先，随机选择K个初始质心，其中K是用户指定的参数，即所期望的簇的个数。然后将数据集中的每个点指派到最近的质心，而指派到一个质心的点即为一个簇。然后，根据指派到的点，将每个簇的质心更新为该簇所有点的平均值。重复指派和更新步骤，知道簇不发生变化，或等价地，知道质心不发生变化。

该过程如下图所示，该图显示如何从3个质心处罚，通过12次指派和更新，找出最后的簇。质心用符号“x”指示；属于同一簇的所有点具有相同颜色的标记。

 

1. K-均值算法的python实现

根据k均值算法的工作流程，我们可以写出伪代码：

创建k个点作为初始质心（通常是随机选择）
当任意一个点的簇分配结果发生改变时:
　　对数据集中的每个点:
　　　　对每个质心:
      　　　　计算质心与数据点之间的距离
   　　将数据点分配到据其最近的簇
   对每个簇，计算簇中所有点的均值并将均值作为新的质心
直到簇不再发生变化或者达到最大迭代次数

在伪代码中，有提到“最近”的说法，那就意味着要进行某种距离的计算。附录1中有总结几种距离度量的方法。这里我们使用的是最简单的欧式距离。

1.1 导入数据集

以经典的鸢尾花数据集为例，来帮助我们建模。

import numpy as np
import pandas as pd
import matplotlib as mpl
import matplotlib.pyplot as plt

#导入数据集
iris = pd.read_csv('iris.txt',header = None)
iris.head()
iris.shape

1.2 构建距离计算函数

我们需要定义一个两个长度相等的数据之间欧式距离计算函数，在不直接应用计算距离计算结果，只比较距离远近的情况下，我们可以用距离平方和代替距离进行比较，化简开平方运算，从而减少函数计算量。

此外需要说明的是，涉及到距离计算的，一定要注意量纲的统一。如果量纲不统一的话，模型极易偏向量纲大的那一方。附录2总结了一些归一化的方法。此处选用鸢尾花数据集，基本不需要考虑量纲问题。

def distEclud(arrA, arrB):
    """
        函数功能：计算两个数据集之间的欧式距离
        输入：两个array数据集
        返回：两个数据集之间的欧氏距离（此处用距离平方和代替距离）
    """
    d = arrA - arrB
    dist = np.sum(np.power(d, 2), axis=1)
    return dist

1.3 编写自动生成随机质心的函数

在定义随机质心生成函数是，首先需要计算每列数据的范围，然后从该范围中随机生成指定个数的质心。此处我们使用numpy.random.uniform()函数生成随机质心。

def randCent(dataSet, k): 
    """
        函数功能：随机生成k个质心
        参数说明：
             dataSet:包含标签的数据集
             k：簇的个数
        返回：
             data_cent：K个质心
    """
    n = dataSet.shape[1]
    data_min = dataSet.iloc[:, :n-1].min()
    data_max = dataSet.iloc[:, :n-1].max()
    data_cent = np.random.uniform(data_min,data_max,(k, n-1))
    return data_cent

1.4 编写K-Means聚类函数

在执行Kmeans的时候，需要不断的迭代质心，因此我们需要两个可迭代容器来完成该目标;

① 第一个容器用于存放和更新质心，该容器可考虑使用list来执行，list不仅是可迭代对象，同时list内不同元素索引位置也可用于标记和区分各质心，即各簇的编号；

② 第二个容器则需要记录，保存和更新各点到质心之间的距离，并能够方便对其进行比较，该容器考虑使用一个三列的数组来执行，其中第一列用于存放最近一次计算完成后某点到各质心的最短距离，第二列用于记录最近一次计算完成后根据最短距离得到的代表对应质心的数据索引，即所属簇，即质心的编号，第三列用于存放上一次某点所对应质心编号（某点所属簇），后两列用于比较质心发生变化后某点所属簇的情况是否发生变化。

def kMeans(dataSet, k, distMeas=distEclud, createCent=randCent):
    """
        函数功能：k-均值聚类算法
        参数说明：
             dataSet：带标签数据集
             k:簇的个数
             distMeas:距离计算函数
             createCent:随机质心生成函数
        返回：
             centroids:质心
             result_set:所有数据划分结果
"""
    m,n = dataSet.shape
    centroids = createCent(dataSet, k)
    clusterAssment = np.zeros((m,3))
    clusterAssment[:, 0] = np.inf
    clusterAssment[:, 1: 3] = -1
    result_set = pd.concat([dataSet, pd.DataFrame(clusterAssment)], axis=1, ignore_index = True)
    clusterChanged = True
    while clusterChanged:
        clusterChanged = False
        for i in range(m):
            dist = distMeas(dataSet.iloc[i, :n-1].values, centroids)
            result_set.iloc[i, n] = dist.min()
            result_set.iloc[i, n+1] = np.where(dist == dist.min())[0]
        clusterChanged = not (result_set.iloc[:, -1] == result_set.iloc[:, -2]).all()
        if clusterChanged:
            cent_df = result_set.groupby(n+1).mean()
            centroids = cent_df.iloc[:,:n-1].values
            result_set.iloc[:, -1] = result_set.iloc[:, -2]
    return centroids, result_set

鸢尾花数据集带进去，查看模型运行效果：

 

2. 算法验证

3. 误差平方和SSE计算

三、模型收敛稳定性探讨

四、二分K-均值算法

1. 二分K均值的python实现

1.1 数据准备

1.2 构建辅助函数

1.3 构建二分K均值函数

五、聚类模型的评价指标

1. 误差平方和SSE

2. 轮廓系数

2.1 凝聚度和分离度

2.2 凝聚度和分离度的基本性质

2.3 轮廓系数

3. 轮廓系数的python实现

【附录1】聚类类模型中距离的确定

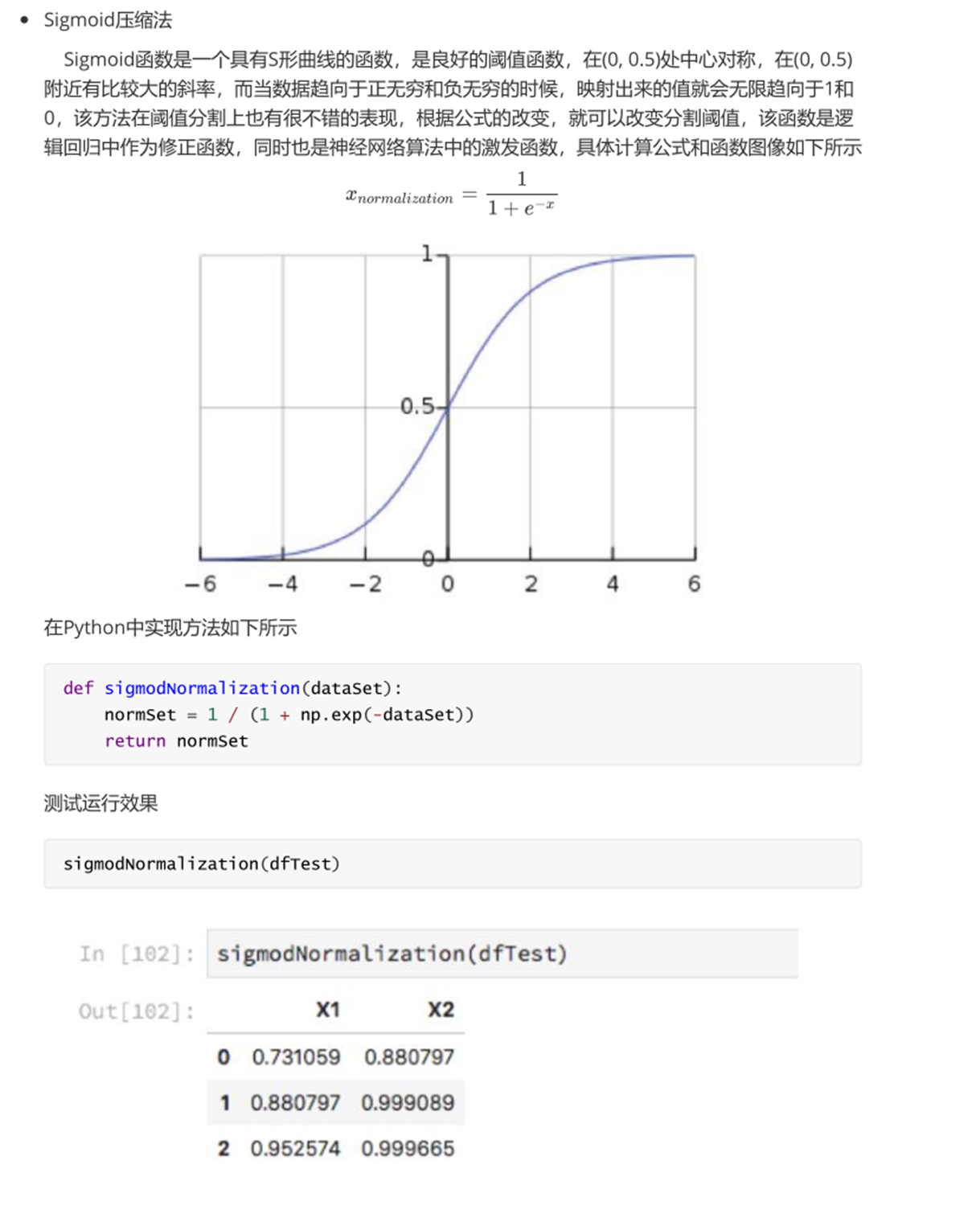
【附录2】归一化方法

六、利用sklearn库中的Kmeans算法进行数据分析案例

1. 随机数据集分析

① 首先创建一个明显分为2类20*2的例子（每一列为一个变量共2个变量，每一行为一个样本共20个样本）

import numpy as np
c1x=np.random.uniform(0.5,1.5,(1,10))
c1y=np.random.uniform(0.5,1.5,(1,10))
c2x=np.random.uniform(3.5,4.5,(1,10))
c2y=np.random.uniform(3.5,4.5,(1,10))
x=np.hstack((c1x,c2x))
y=np.hstack((c2y,c2y))
X=np.vstack((x,y)).T
print(X)

② 引用Python库将样本分为两类（k=2），并绘制散点图：

#只需将X修改即可进行其他聚类分析

import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
 
kemans=KMeans(n_clusters=2，algorithm='elkan')    # algorithm默认是报错 'NoneType' object has no attribute 'split'
result=kemans.fit_predict(X) #训练及预测 
print(result)   #分类结果

plt.rcParams['font.family'] = ['sans-serif']
plt.rcParams['font.sans-serif'] = ['SimHei'] #散点图标签可以显示中文
 
x=[i[0] for i in X]
y=[i[1] for i in X]
plt.scatter(x,y,c=result,marker='o')
plt.xlabel('x')
plt.ylabel('y')
plt.show()

③ 如果K值未知，可采用肘部法选择K值（假设最大分类数为9类，分别计算分类结果为2-9类的平均离差，离差的提升变化下降最抖时的值为最优聚类数K）：

import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from scipy.spatial.distance import cdist
 
K=range(2,10)      # k值为1时报错 'NoneType' object has no attribute 'split'
meanDispersions=[]
for k in K:
    kemans=KMeans(n_clusters=k, algorithm='elkan')
    kemans.fit(X)
    #计算平均离差
    m_Disp=sum(np.min(cdist(X,kemans.cluster_centers_,'euclidean'),axis=1))/X.shape[0]
    meanDispersions.append(m_Disp)
 
plt.rcParams['font.family'] = ['sans-serif']
plt.rcParams['font.sans-serif'] = ['SimHei'] #使折线图显示中文
 
plt.plot(K,meanDispersions,'bx-')
plt.xlabel('k')
plt.ylabel('平均离差')
plt.title('用肘部方法选择K值')
plt.show()

 

从平均离差下降趋势来看，分组为2类最合适。

2. 对某网站500家饭店价格及评论进行聚类

import numpy as np
from sklearn.cluster import KMeans
from scipy.spatial.distance import cdist
import matplotlib.pyplot as plt
import pandas as pd
 
data=pd.read_excel('data.xlsx',header=0).iloc[:501,3:5]
per_25=data.describe().iloc[4,1]
per_75=data.describe().iloc[6,1]
data=data[(data.iloc[:,1]>=per_25)&(data.iloc[:,1]<=per_75)] #选择位于四分位数之内的数
X=np.array(data)

K=range(2,10)
meanDispersions=[]
for k in K:
    kemans=KMeans(n_clusters=k)
    kemans.fit(X)
    meanDispersions.append(sum(np.min(cdist(X,kemans.cluster_centers_,'euclidean'),axis=1))/X.shape[0])

plt.rcParams['font.family'] = ['sans-serif']
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.plot(K,meanDispersions,'bx-')
plt.xlabel('k')
plt.ylabel('平均离差')
plt.title('用肘部方法选择K值')
plt.show()

# 具体聚类过程
 
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
 
kemans=KMeans(n_clusters=3)
result=kemans.fit_predict(X)
print(result)
x=[i[0] for i in X]
y=[i[1] for i in X]
plt.scatter(x,y,c=result,marker='o')
plt.xlabel('avgPrice')
plt.ylabel('llCommentNum')
plt.title('对500家饭店价格与评论数进行聚类')

聚类结果：

[2 0 0 0 0 1 0 0 2 0 0 2 1 2 0 1 2 0 2 2 2 0 0 0 0 1 2 0 1 0 0 2 2 2 2 2 2

 2 2 0 1 0 0 0 1 0 2 2 0 2 2 0 0 2 2 2 1 0 1 1 1 0 0 0 0 1 2 1 2 0 2 1 0 0

 2 1 1 0 0 1 2 2 0 2 2 1 0 2 1 0 2 0 0 1 0 0 1 1 1 0 0 0 0 0 0 0 0 2 1 2 1

 1 0 0 1 0 1 2 1 0 1 1 0 1 1 0 1 0 2 1 1 0 1 0 2 0 2 1 2 1 1 0 0 1 0 1 0 1

 0 2 0 1 1 0 1 0 0 1 1 1 1 0 0 0 0 1 0 0 0 2 0 1 1 0 1 0 1 0 0 0 0 1 1 0 1

 2 0 1 1 2 0 1 0 0 1 1 1 1 1 0 0 0 1 1 1 2 0 1 1 1 2 2 0 0 2 1 1 2 1 1 1 0

 1 1 0 1 2 2 0 2 2 2 0 1 0 1 1 2 1 1 1 0 1 1 1 1 0 0 0 0 1]